Van 3D naar 2D

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Meetkundige berekeningen > Van 3D naar 2D > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Meetkundige berekeningen > Van 3D naar 2D > Uitleg

Lees eerst de Uitleg goed door.

  1. Bekijk het probleem in de Uitleg.
    1. Waarom is het handig om een geschikte doorsnede te tekenen?
    2. Laat met een berekening zien, dat `PT = QT = sqrt(300)`.
    3. Waarom zijn de driehoeken `QST` en `MRT` gelijkvormig?
    4. Je weet dat `|MS| = r`. Laat zien dat `|TM| = sqrt(200) - r`.
    5. Bereken nu `r`.

  2. Bij de vorige opgave is het werken met gelijkvormigheid niet echt noodzakelijk. Je kunt ook werken met goniometrie en bijvoorbeeld `/_Q` uitrekenen. Laat zien, hoe je zo `r` berekent.

  3. Een ander probleem is: Hoeveel bedraagt de afstand van deze bol tot de ribben van de piramide?
    1. Nu is `Delta ACT` een geschikte doorsnede om de gevraagde afstand uit te rekenen. Waarom?
    2. Teken zelf die driehoek op schaal en teken de cirkel die de bol voorstelt er in. (De straal heb je in de voorgaande opgaven uitgerekend.)
    3. Geef in je figuur de gevraagde afstand aan.
    4. Bereken de gevraagde afstand.

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Meetkundige berekeningen > Van 3D naar 2D > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

  1. Bekijk Voorbeeld 1.
    1. Teken de twee driehoeken waarin je gaat rekenen. Bereken eerst TS om goede figuren op schaal te kunnen tekenen.
    2. Zet nu alle bekende afmetingen in je figuren.
    3. Gebruik `Delta SBT` om de breedte van de kamer te berekenen.
    4. Gebruik `Delta SRT` om de lengte van de kamer te berekenen.

  2. Bekijk de zolderverdieping van de twee-onder-één-kap woning van Voorbeeld 1 nog eens. Wil je de dakoppervlakte berekenen (bijvoorbeeld omdat er een nieuwe dakbedekking nodig is), dan gebruik je een uitslag van de figuur.
    1. Teken de uitslag op schaal 1:200.
    2. Bereken de oppervlakte van het dak van deze zolderverdieping.

  3. Bekijk Voorbeeld 2. In de figuur hieronder zie je cirkelboog `ATC` in een assenstelsel.



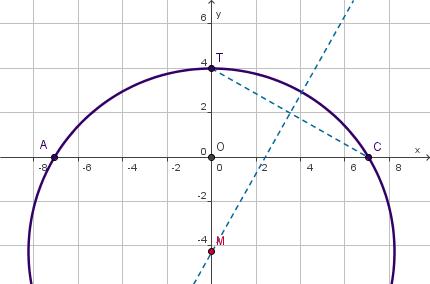
    1. Laat zien dat `A = (-5 sqrt(2),0)` en `C = (5 sqrt(2),0)`.
    2. Stel een vergelijking op van de middelloodlijn van `CT`.
    3. Bereken de coördinaten van punt M door deze middelloodlijn de snijden met de `y`-as.
    4. Beantwoord nu de twee vragen die in Voorbeeld 2 zijn gesteld.

  4. De hoek die boog `ATC` met het vlak `ABCD` maakt, is de hoek tussen deze cirkelboog en de `x`-as.
    Bereken deze hoek in graden nauwkeurig.

  5. Je zou het probleem van Voorbeeld 2 ook kunnen aanpakken met gelijkvormige driehoeken. Noem het midden van `CT` bijvoorbeeld `S`. `MS` is de middelloodlijn van `CT`.
    1. Leg uit waarom de driehoeken `OCT` en `SMT` gelijkvormig zijn.
    2. Laat zien hoe je op die manier TM berekent.

Verwerken

  1. Basketbalbord

    Hier zie je vier momentopnamen van het neerlaten van een basketbalbord.



    De stellage bestaat uit een frame met een rechthoekig bord waaraan de basket bevestigd is. Een basket is een ijzeren ring met een netje. Twee even lange kettingen dienen als beveiliging tegen vallen of te ver zakken van het geheel. Het zijaanzicht van het frame is een parallellogram `ABCD`.
    `BC = 90` cm en `AB = 100` cm.
    In de gymzaal waarin de foto’s zijn genomen zit bevestigingspunt `B` op een hoogte van 280 cm van de begane grond. Eén van de kettingen is bevestigd in `A` en `C`. De ketting is zo lang dat bij het neerlaten van de stellage punt `A` niet lager kan komen dan 250 cm boven de begane grond.
    1. Bereken de lengte van de ketting `AC` in cm nauwkeurig.
    2. Het frame wordt helemaal vanaf de laagste stand omhoog getrokken tot aan de muur. Tijdens deze beweging beschrijft punt `A` een cirkelboog. Bereken de lengte van de baan die punt `A` aflegt.
    3. Bereken de afstand van punt `A` tot de muur op het moment dat `A` op 300 cm boven de begane grond zit.
    4. De afstand `a` tussen de stangen `AB` en `CD` is de lengte van het kortste lijnstuk tussen beide. Deze lengte hangt af van de grootte van hoek `beta`. Druk die afstand `a` uit in `beta`.
    5. Hoe ver zit punt `A` van de muur op het moment dat deze afstand `a` precies 45 cm is?

  2. Kanteldeur

    In de figuur hiernaast is een deel te zien van een kanteldeur van een garagebox. In figuur hieronder is een schematische tekening gemaakt van het zijaanzicht van deze deur. De kanteldeur is door middel van een metalen frame aan de muur bevestigd.
    `PD` en `PQ` zijn twee onderdelen van dat frame. Bij het sluiten en openen van de kanteldeur glijdt het hoekpunt `A` van deze deur langs de horizontale rail `PQ`. Het hoekpunt `B` van de deur is via een metalen arm `BC` verbonden met het midden `M` van `PD`. Bij het sluiten en openen doorloopt `B` een halve cirkel, evenals punt `C`. Dit punt `C` is door middel van een veer `CE` verbonden met punt `D` op de grond. Deze veer zorgt voor tegenwicht zodat de deur bij sluiten en openen hanteerbaar blijft.
    Enige gegevens:


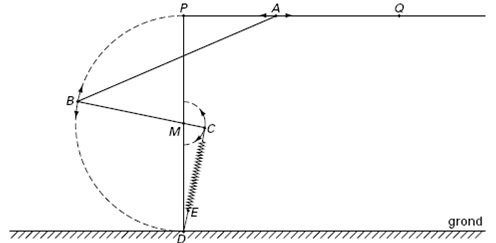
    Breng een rechthoekig `Oxy`-assenstelsel aan, zodat dat de oorsprong punt `D` is, de `x`-as over de grond loopt evenwijdig met `PQ` en `PD` op de `y`-as ligt. De eenheid op beide assen is 1 dm.
    1. Stel een vergelijking op van de cirkel die punt `B` voor de helft doorloopt.
    2. Een aanhangwagentje, geparkeerd in de garage, is 6 dm hoog. Bereken de afstand van punt `B` tot lijnstuk `PD` als de kanteldeur `AB` in de stand staat waarbij het wagentje er nog net onderdoor kan rijden.
    3. Bereken de lengte van `PA` als de afstand van punt `B` tot lijnstuk `PD` zo groot mogelijk is.

Testen

  1. Trailertafel

    De tafel op deze foto bestaat uit een rechthoekig blok en een glazen plaat in de vorm van een kwart cirkel. De glazen plaat is gemonteerd op een metalen buizenconstructie met drie poten. Eén van de poten is bevestigd in het blok. De afstand van deze poot tot de twee dichtstbijzijnde ribben van het blok is 20 cm; de afstand tot de rechte zijden van de glasplaat is ook 20 cm. Enkele maten van blok en glasplaat zijn aangegeven in het bovenaanzicht in de linker figuur hieronder. In deze opgave wordt de dikte van de poten verwaarloosd. In de rechter figuur is dit schematisch aangegeven. `P`, `Q` en `R` zijn de punten op de glasplaat recht boven de poten. De glasplaat kan draaien om de poot in het blok (onder het punt `Q`).

        

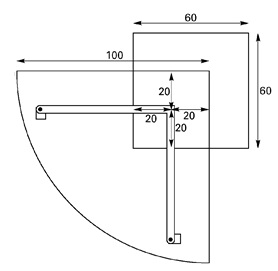
    1. Bereken hoe lang `PQ` en `RQ` in minimaal moeten zijn om draaien van de glasplaat over 360° mogelijk te maken. Rond je antwoord naar boven af op een geheel aantal centimeters.
    Als de glasplaat gaat draaien om punt `Q` dan beschrijven de twee punten op de glasplaat die het verst van `Q` af liggen dezelfde cirkel `c` met middelpunt `Q`. Breng een assenstelsel aan met als oorsprong punt `Q` en de assen evenwijdig aan de zijden van het bovenvlak van het rechthoekige blok waar de tafel op gemonteerd is.
    1. Stel een vergelijking op van cirkel `c`.
    In een kamer wordt de tafel met een zijvlak van het blok tegen een muur gezet zo, dat punt `Q` dan 40 cm van de muur afligt. Er zijn twee punten `A` en `B` waar de glasplaat tegen de muur kan komen.
    1. Bereken de afstand tussen de twee punten `A` en `B` waar de glasplaat tegen de muur kan komen. Geef je antwoord in gehele centimeters nauwkeurig.
    2. Als de glasplaat tegen de muur rust, dan maakt de cirkelvormige rand van de glasplaat een bepaalde hoek met de muur. Bereken de grootte van die hoek in graden nauwkeurig.