Inproduct

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectormeetkunde > Inproduct > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectormeetkunde > Inproduct > Uitleg

Lees eerst de beide pagina's van de Uitleg goed door.

  1. Bekijk de Uitleg. Neem nu de vectoren `vec(a) = ((-2),(3))` en `vec(b) = ((2),(1))`.
    1. Bereken de lengtes en de richtingshoeken van beide vectoren.
    2. Bepaal nu de hoek `phi` tussen beide vectoren en bereken het inproduct met behulp van `vec(a) * vec(b) = |vec(a)| * |vec(b)| * cos(phi)`.
    3. Op pagina 2 van de Uitleg zie je dat je het inproduct van `vec(a)` en `vec(b)` ook kunt berekenen vanuit hun kentallen. Het inproduct is dan `a_x * b_x + a_y * b_y`. Bereken ook op die manier het inproduct van de gegeven vectoren en ga na dat je hetzelfde vindt als bij b.
    4. Je kunt met behulp van het antwoord van c en `vec(a) * vec(b) = |vec(a)| * |vec(b)| * cos(phi)` de hoek `phi` tussen beide vectoren berekenen. Laat zien hoe.

  2. Neem nu de vectoren `vec(a) = ((1),(-5))` en `vec(b) = ((-3),(-2))`.
    1. Bereken het inproduct van beide vectoren met behulp van hun kentallen.
    2. Gebruik dit inproduct om de hoek `phi` tussen `vec(a)` en `vec(b)` te berekenen.

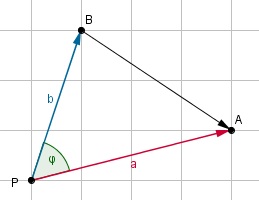  3. Je kunt de formule `vec(a) * vec(b) = a_x * b_x + a_y * b_y` ook afleiden met behulp van de cosinusregel.
    In de figuur zie je `vec(a)`, `vec(b)` en `vec(a) - vec(b)` getekend. De eindpunten van `vec(a)` en `vec(b)` zijn `A` en `B`, het beginpunt van beide vectoren is `P`. In `Delta PAB` geldt de cosinusregel: `|AB|^2 = |PA|^2 + |PB|^2 - 2 * |PA| * |PB| * cos(phi)`.
    1. Laat zien dat `|PA|^2 = a_x^2 + a_y^2`, `|PB|^2 = b_x^2 + b_y^2` en `|PA|^2 = (a_x - b_x)^2 + (a_y - b_y)^2`
    2. Vul dit in de cosinusregel in. Herleid de uitdrukking tot `a_x b_x + a_y b_y = sqrt(a_x^2 + a_y^2) sqrt(b_x^2 + b_y^2) cos(phi)`.
    3. Leg uit waarom je hiermee de juiste uitdrukking hebt gevonden.

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectormeetkunde > Inproduct > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

  1. Bekijk Voorbeeld 1. Bereken de hoek tussen `vec(a) = ((-1),(4))` en `vec(b) = ((3),(-2))` in één decimaal nauwkeurig.

  2. Gegeven zijn in een cartesisch assenstelsel de punten `A(10,20)`, `B(15,20)`, `C(16,22)` en `D(14,23)`. Bereken met behulp van vectoren de hoeken van vierhoek `ABCD`.

  3. Gegeven `vec(a) = ((12),(5))`, `vec(b) = ((-15),(36))`, `vec(c) = ((6),(2,5))`, `vec(d) = ((0),(-5))`, `vec(e) = ((13),(0))` en `vec(f) = ((10),(-24))`.
    1. Gebruik eerst de applet van Voorbeeld 2 om te bekijken wanneer het inproduct van twee vectoren gelijk is aan het product van hun lengtes.
    2. Van welke van deze vectoren is het inproduct gelijk aan het product van hun lengtes? Hoe kun je dat aan hun kentallen zien?
    3. Gebruik eerst de applet van Voorbeeld 2 om te bekijken wanneer het inproduct van twee vectoren 0 is.
    4. Van welk van deze vectoren is het inproduct 0? Hoe kun je dat aan hun kentallen zien?

  4. In Voorbeeld 3 zijn in een cartesisch assenstelsel de punten `A(10,20)`, `B(15,20)`, `C(16,22)` en `D(14,23)` gegeven. Toon aan dat vierhoek `ABCD` een vlieger is door te laten zien dat beide diagonalen loodrecht op elkaar staan en dat diagonaal `AC` de andere diagonaal doormidden deelt.

Verwerken

  1. Bereken de hoek tussen `vec(a) = ((-2),(5))` en `vec(b) = ((3),(1))` in graden nauwkeurig.

  2. Bereken in graden nauwkeurig de hoeken van `Delta PQR` als `P(-5,10)`, `Q(7,7)` en `R(0,12)`.

  3. Bootje in sloot

    Een bootje wordt door een jongen en een twee keer zo sterke man door het midden van een sloot getrokken. De jongen en de man lopen ieder aan een andere kant van de sloot. De boot blijft in het midden van de sloot varen. De man trekt met een kracht van 10 N en onder een hoek van 20° met de vaarrichting.
    1. Laat in een bovenaanzicht de vectoren zien die de twee trekkrachten voorstellen.
    2. Welke arbeid verrichten beiden samen als ze het bootje 1 km voorttrekken?
    3. Verrichten ze evenveel arbeid?

  4. Gelijkbenige driehoek

    Elke gelijkbenige driehoek kan door een goede keuze van het assenstelsel de hoekpunten `A(-a,0)`, `B(a,0)` en `C(0,c)` hebben (`a` en `c` beide positief).
    Toon met behulp van het inproduct aan dat de zwaartelijn uit `C` bissectrice is van `/_C`.

Testen

  1. Bereken de hoek tussen `vec(u) = ((12),(10))` en `vec(v) = ((-8),(16))` in graden nauwkeurig.

  2. Gegeven is de vlieger `PQRS` door `P(12,0)`, `Q(5,6)`, `R(0,6)` en `S(3,2)`.
    1. Bereken `/_PQR` in graden nauwkeurig.
    2. Toon aan dat in deze vlieger de diagonalen loodrecht op elkaar staan.