Vectoren en kentallen

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectormeetkunde > Vectoren en kentallen > Inleiding

Probeer de vraag bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectormeetkunde > Vectoren en kentallen > Uitleg

Lees eerst de Uitleg goed door.

1. Bekijk de Uitleg nog eens.
   1. Laat zien hoe je aan de lengtes van de verplaatsingen komt.
   2. Bepaal de kentallen van `vec(v_2)`.
   3. Bepaal hieruit de kentallen van `vec(r)`.
   4. Welke lengte en welke richtingshoek heeft `vec(r)`?


2. Bereken hoeveel km hetzelfde vliegtuig zich naar het Westen en het Zuiden heeft verplaatst als het eerst 30 minuten met 240 km/h onder 330° t.o.v. het Oosten en vervolgens 40 minuten met een snelheid van 210 km/h en een koershoek van 60° t.o.v. het Oosten vliegt.
   

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectormeetkunde > Vectoren en kentallen > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

3. Bekijk Voorbeeld 1. Je kunt met de applet de vectoren `vec(a) = ((1),(2))` en `vec(b) = ((3),(-1))` kunt optellen, aftrekken en vermenigvuldigen met een getal
   1. Maak `vec(a) - vec(b)` en geef de kentallen van deze vector.
   2. Maak `vec(b) - vec(a)` en geef de kentallen van deze vector.
   3. Maak `2 * vec(a) + vec(b)` en geef de kentallen van deze vector. Bereken ook de lengte van deze vector.
   4. Maak `0,5 * vec(a) - vec(b)` en geef de kentallen van deze vector. Bereken ook de lengte van deze vector.


4. Bekijk nu Voorbeeld 2. Je kunt met deze applet hetzelfde doen als die in voorbeeld 1, alleen wordt nu de parallellogramconstructie gebruikt.
   Voer de opdrachten in de vorige opgave nog eens uit, maar nu met deze manier van werken.
   


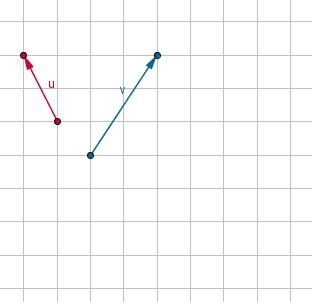5. Hier zie je de vectoren `vec(u) = ((-1),(2))` en `vec(v) = ((2),(3))`. Gebruik eventueel de applet in Voorbeeld 3.
   1. Teken de vector `vec(u) + vec(v)`. Gebruik de "staart aan kop" methode.
   2. Teken de vector `vec(u) + vec(v)`. Gebruik een parallellogramconstructie.
   3. Teken de vector `2 * vec(u)`.
   4. Teken de vector `2 vec(u) + 1,5 vec(v)`. Gebruik ook nu beide manieren van tekenen van een somvector.
   5. Teken de vector `-2 vec(v)`.
   6. Teken de vector `vec(u) - 2 vec(v) = vec(u) + (-2 vec(v)))`.


6. Bepaal van alle vectoren uit de vorige opgave de kentallen en bereken hun lengtes.
   


7. Oefen met andere vectoren `vec(u)` en `vec(v)`. Gebruik de applet van Voorbeeld 3. Bereken de vectoren `vec(u) + 2 vec(v)`, `0,5 vec(u) - vec(v)`, en nog een aantal vectoren en bereken hun lengtes. Werk samen met een medeleerling.
   


8. In een cartesisch assenstelsel `Oxy` zijn gegeven de punten `A`, `B` en `C`. Deze drie punten liggen niet op één lijn.
   1. Leg uit waarom `vec(AB) = vec(OB) - vec(OA)`.
   2. Leg uit waarom `vec(AB) = - vec(BA)`.
   3. Leg uit waarom `vec(AB) = vec(AC) - vec(BC)`.
   4. Leg uit waarom de afstand tussen `A` en `B` gelijk is aan `|vec(OB) - vec(OA)|`.
   Neem nu aan dat `A(0,2), B(5,3)` en `C(3,6)`.
   5. Laat ook zien dat de uitspraken in a, b, c en d kloppen door met de kentallen van de vectoren te werken.


9. Vectoren worden in de natuurkunde gebruikt om krachten weer te geven. Gegeven zijn twee krachten die op een lichaam werken. `vec(F_1)` heeft een grootte van 10 N en `vec(F_2)` heeft een grootte van 8 N. De hoek tussen beide krachten is 30°. De resultante van beide krachten is `vec(R) = vec(F_1) + vec(F_2)`.
   1. Waarom is het voor het berekenen van de resultante van deze krachten van belang dat ze hetzelfde aangrijpingspunt hebben?
   2. Teken de resultante `vec(R)` van deze beide krachten.
   3. Bereken de lengte van `vec(R)` met behulp van de cosinusregel.
   Je kunt die lengte ook berekenen met behulp van kentallen als je een assenstelsel invoert. Neem het aangrijpingspunt van beide vectoren als oorsprong en leg de `x`-as langs vector `vec(F_1)`.
   4. Welke kentallen hebben beide vectoren nu?
   5. Bereken nu de kentallen van de somvector en de lengte van de somvector. Ga na, dat je hetzelfde vindt als bij c.


10. Vector `vec(a)` heeft een lengte van 5 en een richtingshoek van 35°. Vector `vec(b)` heeft een lengte van 4 en een richtingshoek van 110°.
    1. Teken in een assenstelsel de vectoren `vec(a)`, `vec(b)` en `vec(a) + vec(b)`.
    2. Bereken de kentallen van `vec(a) + vec(b)`.
    3. Bereken de richtingshoek van `vec(a) + vec(b)`.

Verwerken

11. Gegeven zijn de vectoren:
    `vec(a) = ((2),(3))`, `vec(b) = ((-2),(4))` en `vec(c) = ((0),(1))`.
    Bereken nu de kentallen en de lengtes van de vectoren:
    1. `vec(a) + vec(b)`
    2. `vec(a) - 0,5 vec(b)`
    3. `vec(a) + vec(b) + vec(c)`
    4. `2 vec(a) - vec(b) - vec(c)`


12. Gegeven zijn in een cartesisch assenstelsel de punten `A(10,20)`, `B(15,20)`, `C(16,22)` en `D(14,23)`. Bewijs met behulp van vectoren dat vierhoek `ABCD` een vlieger is.
    



13. Laurel en Hardy

    Een bekende stomme film is die waarin Stan Laurel en Oliver Hardy een piano vervoeren. Ze staan daarin ieder aan een kant tegen de piano te duwen. Oliver merkt dat er geen beweging in komt, dus hij gaat van opzij duwen. Ze duwen beiden met een kracht van 6 newton. Hier zie je in de linkerfiguur een bovenaanzicht van de situatie.
    
            
    
    
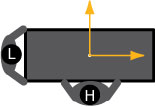
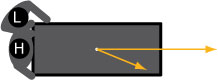
    1. Teken de richting waarin de piano volgens jou gaat bewegen, aangenomen dat de wrijving met de vloer in alle richtingen even groot is.
    2. Beiden gaan daarna de piano duwen volgens het bovenaanzicht dat je in de rechter figuur ziet. Oliver duwt nu twee keer zo hard als Stan. Maak zelf een bovenaanzicht van deze situatie. Neem voor de hoek tussen beide krachten 30°. Teken ook nu weer de richting waarin de piano gaat bewegen.



14. Route in een fjord

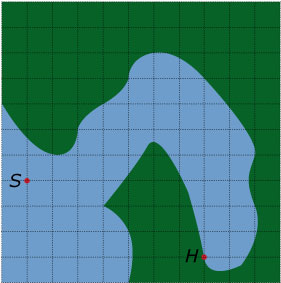    Een vrachtboot `S` ligt voor de ingang van een fjord. Hij moet naar de haven `H` om te lossen. Eén hokje is 500 m bij 500 m.
    1. Teken een route met zo weinig mogelijk koerswijzigingen.
    2. Meet de richtingshoek van de vector van `S` naar `H` en vergelijk die met de som van de richtingshoeken van de routevectoren. Welke conclusies kun je trekken? Hoe zit dat met de lengtes van de betrokken vectoren?
    3. Leg uit waarom in dit voorbeeld de somvector aan de éne kant wel en aan de andere kant toch ook weer niet als resultante van de delen gezien kan worden.

Testen

15. Gegeven zijn de vectoren:
    `vec(a) = ((-5),(10))`, `vec(b) = ((12),(7))`,`vec(c) = ((3),(-2))`,`vec(d) = ((0),(5))`,`vec(e) = ((-4),(0))` en `vec(f) = ((20),(-50))`.
    Bereken nu de kentallen en de lengtes van de vectoren:
    1. `vec(a) - vec(b)`
    2. `vec(b) + 2 vec(c)`
    3. `5 vec(d) - vec(e) + vec(f)`
    4. `vec(b) + 0,2 vec(f)`


16. A en B trekken een wagentje voort aan twee touwen die beide aan het midden van de voorkant van het wagentje zijn bevestigd. De hoek tussen beide touwen is 90°.
    1. Teken de resulterende kracht en bereken hoe groot hij is als beide trekken met een kracht van 6 newton.
    2. Voer de vorige opdracht nog eens uit als A met een kracht van 8 newton en B met een kracht van 6 newton trekt.