Totaalbeeld

Samenvatten

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Hoeken en afstanden > Totaalbeeld > Samenvatten


Je hebt nu het onderwerp Hoeken en afstanden doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

Begrippenlijst:

  1. een kwadraat afsplitsen
  2. raaklijn aan een cirkel, raakpunt
  3. de hoek tussen een lijn en een cirkel, tussen twee cirkels
  4. de afstand van een punt tot een lijn, van een punt tot een cirkel, tussen twee evenwijdige lijnen en van een lijn tot een cirkel

Activiteitenlijst:

  1. door kwadraat afsplitsen middelpunt en straal van een cirkel bepalen
  2. nagaan of een lijn een cirkel snijdt, raakt of mijdt — met behulp van de discriminantmethode een vergelijking opstellen van een lijn die een cirkel raakt of een cirkel die een lijn raakt
  3. met behulp van de loodrechte stand van raaklijn en straal naar raakpunt de vergelijking van een raaklijn aan een cirkel opstellen — de hoek tussen een lijn en een cirkel en tussen twee cirkels berekenen
  4. de afstand berekenen tussen twee punten, van een punt tot een lijn of een cirkel en van een lijn tot een evenwijdige lijn of een cirkel

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Hoeken en afstanden > Totaalbeeld > Achtergronden


Testen

Opgaven

  1. Gegeven zijn de cirkels `c_1: x^2 + y^2 = 12x - 10` en `c_2` met middelpunt `M_2(4, 2)` en straal `sqrt(10)`.
    1. Bereken het middelpunt en de straal van `c_1`.
    2. Bereken de snijpunten van `c_1` en `c_2`.
    3. Bereken de afstand van `M_2` tot cirkel `c_1`.
    4. Bereken de hoek waaronder beide cirkels elkaar snijden in graden nauwkeurig.
    5. Door `A(0,4)` gaan twee lijnen die `c_2` raken. Stel van elk van deze twee lijnen een vergelijking op.
    6. De raaklijn aan `c_1` in het punt `P(7, 5)` snijdt de `x`-as in `Q`. Bereken de coördinaten van `Q`.
    7. Bereken de afstand van lijn `PQ` tot punt `M_2`.

  2. De afstand van een punt tot een lijn kun je ook berekenen met behulp van een cirkel. Neem `O(0,0)` en `l: x + 2y = 6`.
    1. Stel een vergelijking op van de cirkel `c` met middelpunt `O` en straal `r`.
    2. `l` moet raken aan `c`. Bepaal de waarde van `r` met behulp van de discriminantmethode.
      3. Je kunt de gevraagde afstand ook berekenen door te werken met gelijkvormige driehoeken. Daarbij gebruik je de snijpunten van `l` met de twee assen. Noem het snijpunt van `l` met de `x`-as `A` en dat met de `y`-as `B`. `OC` is het lijnstuk dat de afstand van `O` tot `l` voorstelt.
    3. Bereken nu `|OC|` met behulp van gelijkvormigheid.
      4. Neem nu voor `l` een willekeurige lijn `ax + by = c`.
    4. Laat zien dat: `d(O,l) = |c/sqrt(a^2+b^2)|`
    5. Gebruik deze formule om de afstand van `O` tot `l: x + 2y = 6` uit te rekenen.

  3. Cirkel `c` snijdt van de lijn `y = 4` een lijnstuk met lengte 4 af, gaat door `P(-5, 2)` en heeft een middelpunt `M` op de `x`-as. Stel een vergelijking op van `c`.

  4. Een bol met straal 12 `cm` ligt in een vaas waarvan de open binnenkant een zuivere kegelvorm van hoogte 30 `cm` en diameter 30 `cm` heeft. De vraag is: Steekt de bol boven de bovenrand van de vaas uit? En zo ja hoeveel? Je lost dit probleem op door gebruik te maken van analytische meetkunde.
    1. Teken een dwarsdoorsnede van kegel en bol in een cartesisch assenstelsel. Neem voor de top van de kegel `O(0,0)` en laat de hoogte van de kegel samenvallen met de `y`-as.
    2. Kies voor het middelpunt van de bol `M(0,m)` en stel een bijpassende vergelijking voor de bol op.
    3. Welke twee raaklijnen aan de bol kun je nu gebruiken om het probleem op te lossen?
    4. Bepaal door berekening `m` en bereken hoever de bol boven de kegel uit steekt of hoeveel de rand van de kegel boven de bol zit.
    5. Hoe had je dit probleem zonder analytische meetkunde kunnen oplossen?

  5. Gegeven is de cirkel `c: x^2 + y^2 = 2x + 3` en de lijn `l: y = ax`. De snijpunten van `l` en `c` zijn `A` en `B`.
    1. Neem `a = 2`. Toon aan dat `|OA|*|OB| = 3`.
    2. Bewijs dat voor elke `a` geldt: `|OA|*|OB| = 3`.

Toepassen

  1. Macht van een punt ten opzichte van een cirkel

    Punt `P` ligt buiten een cirkel `c`. Er zijn twee lijnen door `P` die de cirkel raken, één van die lijnen is `l`, het bijbehorende raakpunt is `R`. Verder is `m` een lijn door `P` die de cirkel snijdt in `A` en `B`. Nu geldt: `|PR|^2 = |PA|*|PB|`. Dit kun je met analytische meetkunde bewijzen door `P(0,0)` te kiezen en een cirkel te kiezen met middelpunt `M(2,0)` en straal 1.
    1. Stel een vergelijking op van een mogelijke lijn `l` en bereken het bijbehorende raakpunt `R`.
    2. Neem nu de lijn `m: y = ax` en kies een geschikte waarde van `a`. Bereken de snijpunten `A` en `B`. Bereken `|PR|, |PA|` en `|PB|` en ga na dat: `|PR|^2 = |PA|*|PB|`.
    3. Onderzoek of ook voor andere a geldt: `|PR|^2 = |PA|*|PB|`.
    4. Is je bewijs nu helemaal compleet? Licht je antwoord toe.

  2. Omgeschreven cirkel

    De straal van de omgeschreven cirkel van een gelijkzijdige driehoek met zijden van `a` cm kun je in `a` uitdrukken. Laat zie hoe je dit kunt doen door een geschikt assenstelsel te kiezen.

  3. Deellijn

    De deellijn (of bissectrice) van een hoek is de lijn die de hoek in twee gelijke delen verdeelt. De lijnen `l: y = 0` en `m: y = 2x` maken een scherpe hoek met elkaar. Punt `P(x,y)` is een punt van de deellijn van deze hoek.
    1. Stel een vergelijking op van deze deellijn (benaderingen in drie decimalen nauwkeurig).
    2. Toon aan dat elk punt van deze deellijn dezelfde afstand heeft tot lijn `l` als tot lijn `m`.

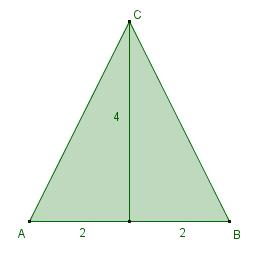
  4. Grootste cirkel uit een driehoek

    Je ziet hier een gelijkbenig driehoekige lap stof. Je wilt er een zo groot mogelijke cirkelvormige lap stof uit snijden. Hoe groot wordt de straal?
    1. Maak een assenstelsel zo, dat `A = (-2,0), B = (2,0)` en `C = (0,4)`.
    2. Het middelpunt van de gevraagde cirkel is `M(0,p)`. `M` moet even ver van de lijnen `AB, BC` en `AC` liggen. Druk `d(M,AB)` en `d(M,BC)` beide uit in `p`.
    3. Bereken `p` en beantwoord de vraag.