Lijnen

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Analytische Meetkunde > Lijnen > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Analytische Meetkunde > Lijnen > Uitleg

Lees eerst de Uitleg goed door.

  1. Bestudeer de Uitleg. Laat zien dat bij de lijn door `A(1, 2)` en `B(4, 1)` de vergelijking `x + 3y = 7` past. Welke richtingscoëfficiënt heeft deze lijn? En wat betekent dit getal?

  2. Laat zien dat de lijn door `A(1, 2)` en `C(1, 4)` niet de vorm `y = ax + b` kan hebben.

  3. Laat zien dat bij de lijn door `A(1, 2)` en `C(1, 4)` de vergelijking `x = 1` past.

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Analytische Meetkunde > Lijnen > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

  1. Bekijk Voorbeeld 1. Teken in een cartesisch assenstelsel `Oxy` de lijn met vergelijking `3x + 4y = 12` en bereken de richtingscoëfficiënt van deze lijn.

  2. Bekijk de algemene vergelijking van een lijn `l: ax + by = c`.
    1. Hoe loopt deze lijn als `a = 0`?
    2. Hoe loopt deze lijn als `b = 0`? Welke richtingscoëfficiënt hoort daar bij?
    3. Welke richtingscoëfficiënt heeft `l` als `a = b`?
    4. Wat is er met `l` aan de hand als `c = 0`?

  3. Teken de volgende lijnen in een `Oxy`-assenstelsel en bereken (indien mogelijk) de richtingscoëfficiënt van de lijn:
    1. `6x - 2y = 13`
    2. `2x = 7`
    3. `15 - 2y = 3x`
    4. `2(x + 2y) = 5`
    5. `y = -5`
    6. `6(y - 1) - 2(3 - x) = x + y - 4`

  4. Waarom beschrijven de vergelijkingen `2x + 4y = 12` en `x + 2y = 6` en `y = -1/2 x + 3` dezelfde lijn?

  5. Bekijk Voorbeeld 2. Stel een vergelijking op van de lijn `l` die gaat door de punten `P(-2, 3)` en `Q(4, 6)`. Bepaal ook de richtingscoëfficiënt van `l` en de snijpunten met de assen.

  6. Stel een vergelijking op van de lijn door `R(-22, -35)` en `S(12, 25)`. Bereken de richtingscoëfficiënt van deze lijn en de snijpunten met de assen.

  7. Stel een vergelijking op van de lijn door `T(38, -15)` met richtingscoëfficiënt -12. Bereken de snijpunten van deze lijn met beide assen.

Practicum

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Analytische Meetkunde > Vergelijkingen van lijnen > GeoGebra II


Maak in GeoGebra de figuur van Voorbeeld 2 na. Door met de rechtermuisknop op de lijn te klikken kun je de vergelijking laten zien. Je ziet in het practicum hoe je ook zelf vergelijkingen kunt invoeren. Dat kun je bij de volgende opgaven goed gebruiken. Bedenk wel dat je de berekeningen ook met de hand moet kunnen uitvoeren.

Verwerken

  1. Gegeven de lijnen `x + y = 6, y = 2x, x - 2y = 4` en `x = 5`.
    1. Teken deze vier lijnen in een cartesisch assenstelsel (in GeoGebra).
    2. Hoeveel roosterpunten liggen er binnen het gebied dat door deze vier lijnen wordt ingesloten?

  2. Gegeven zijn een zestal lijnen door hun vergelijkingen: `l: 7x + 2y = 14, m: -5x = 12, n: 14x = 28 - 4y, p: 7x + 2y = 15, q: 3y = 15 - 7x, r: y = -3 1/2 x + 3`. Beantwoord nu de volgende vragen. Leg steeds uit hoe je te werk gaat.
    1. Welke van deze zes vergelijkingen horen bij evenwijdige lijnen?
    2. Welke van deze zes vergelijkingen horen bij dezelfde lijn?
    3. Welke van deze zes vergelijkingen horen bij een roosterlijn?
    4. Maak deze lijnen in GeoGebra en ga dan na hoe dit programma de vergelijkingen weergeeft (er zijn twee instellingen mogelijk). Onderzoek steeds of de vergelijking die GeoGebra geeft overeen komt met je invoer.

  3. In een cartesisch assenstelsel `Oxy` zijn gegeven de punten `A(2, 0), B(7, 3)` en `C(0, 5)`. (Maak een tekening in GeoGebra.)
    1. Stel een vergelijking op van de lijn `l` door `A` en `B`.
    2. Stel een vergelijking op van de lijn door `C` die evenwijdig is aan `l`.

  4. Gegeven is de lijn `l` met vergelijking `x - 2y = 6`.
    1. Bepaal de vergelijking van de lijn die ontstaat door `l` te spiegelen in de `x`-as.
    2. Bepaal de vergelijking van de lijn die ontstaat door `l` te spiegelen in de `y`-as.
    3. Bepaal de vergelijking van de lijn die ontstaat door `l` te spiegelen in de lijn `y = x`.

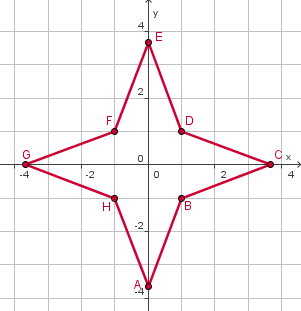  5. Hier zie je een mooie symmetrische ster die bestaat uit 8 even grote lijnstukken. Eén van die lijnstukken ligt op de lijn met vergelijking `8x + 3y = 11`. Eén van de hoekpunten van deze ster is het punt `D(1, 1)`. De hoekpunten `A, C, E` en `G` liggen even ver van `O` af.
    1. Stel vergelijkingen op van de lijnen waarop de andere lijnstukken liggen.
    2. Bereken de coördinaten van de hoekpunten `A, C, E` en `G`.
    3. Bereken de totale omtrek en de totale oppervlakte van de ster.

Testen

  1. De lijn `l` gaat door `A(-10, 45)` en `B(15, -5)`.
    1. Stel een vergelijking op van `l`.
    2. Bereken de richtingscoëfficiënt van deze lijn en de snijpunten met de assen.
    3. Stel een vergelijking op van de lijn door `P(3, 2)` die evenwijdig is met `l`.
    4. Stel een vergelijking op van de lijn `m` die ontstaat door `l` te spiegelen in de `x`-as.
    5. Stel een vergelijking op van de lijn `m` die ontstaat door `l` te spiegelen in de lijn `y = x`.