Eigenschappen van logaritmen

Inleiding

Je hebt nu wel het begrip logaritme leren kennen als oplossing van een exponentiële vergelijking, maar nog geen methode gezien om willekeurige logaritmen rechtstreeks te bepalen (benaderen) met de rekenmachine.
Er zit wel een knop [LOG] op, maar daarmee kun je nog niet meteen voor elk willekeurig grondtal de logaritme van een getal vinden. Je hebt de eigenschappen van logaritmen nodig. Die ga je nu nader bekijken.

Je leert nu:

eigenschappen van logaritmen gebruiken;
logaritmen benaderen met de grafische rekenmachine.

Je kunt al:

werken met het begrip logaritme;
logaritmen bepalen vanuit exponentiële vergelijkingen.

Verkennen

Je weet dat g^x = y gelijkwaardig is met x = ^glog(y). Dat levert alvast twee eigenschappen van logaritmen op.

> Hoe volgt hier uit dat ^glog(g^x) = x?
> Welke andere eigenschap volgt hier rechtstreeks uit?
> Wat gebeurt er als je twee logaritmen optelt, is ^glog(a) + ^glog(b) = ^glog(a + b)?
> En hoe zit het met ^glog(a) – ^glog(b)?

Uitleg

Voor het saldo S op een spaarrekening t jaar na een eenmalige storting van € 4000 en een jaarlijkse rente van 5% geldt: S(t) = 4000 · 1,05^t.
De tijd die nodig is om het saldo te verdubbelen vind je door op te lossen 1,05^t = 2.
De verdubbelingstijd bij een groeifactor van 1,05 is daarom ^1,05log(2).
Zo is de verdrievoudigingstijd te vinden uit 1,05^t = 3.
De verdrievoudigingstijd van het saldo is dus ^1,05log(3).

De verzesvoudigingstijd van het saldo is ^1,05log(6).
Die verzesvoudigingstijd kun je ook vinden door de verdubbelingstijd en de verdrievoudigingstijd op te tellen.
Dit levert op: ^1,05log(6) = ^1,05log(2) + ^1,05log(3).

Ofwel: ^1,05log(2) + ^1,05log(3) = ^1,05log(2 · 3).

De verachtvoudigingstijd van de saldo is ^1,05log(8).
Die verachtvoudigingstijd kun je ook vinden door drie keer de verdubbelingstijd te nemen.
En zo vind je: ^1,05log(8) = 3 · ^1,05log(2).

Ofwel: 3 · ^1,05log(2) = ^1,05log(2³).

Op deze wijze kun je enkele eigenschappen van logaritmen aannemelijk maken.

‡

Opgaven

In de Uitleg werd bekeken in welke tijd een saldo zich verdubbeld dan wel verdrievoudigd.
1. Hoe lang duurt het voor het saldo 2 keer zo groot (dus € 8000,=) geworden is? Schrijf het antwoord als logaritme. Bereken deze logaritme op één decimaal nauwkeurig.
2. Hoe lang duurt het voor het saldo 3 keer zo groot geworden is? Schrijf het antwoord als logaritme. Bereken deze logaritme op één decimaal nauwkeurig.
3. Hoe lang duurt het voor het saldo 6 keer zo groot geworden is? Schrijf het antwoord als logaritme. Bereken deze logaritme op één decimaal nauwkeurig.
4. Het antwoord bij a kun je krijgen door het antwoord bij b van dat bij c af te trekken. Controleer dit en geef een verklaring.
5. Bij d heb je een voorbeeld van een eigenschap van logaritmen die in de Theorie staan vermeld. Om welke eigenschap gaat het hier?

Bij exponentiële afname komt het begrip halveringstijd voor.
1. Geef een omschrijving van het begrip halveringstijd. Maak hierbij gebruik van een logaritme.
2. Bereken in maanden nauwkeurig de halveringstijd in het geval een hoeveelheid jaarlijks met 7% afneemt.
3. De radioactieve stof Strontium heeft een halveringstijd van 28 jaar. Bereken in drie decimalen nauwkeurig de groeifactor per jaar.

Theorie

Definitie logaritme:
g^x = y is gelijkwaardig met x = ^glog(y) als 0 < g < 1 of g > 1 en als a > 0.

Definitieformules:
Uit de definitie van logaritme volgt: ^glog(g^x) = x en g^{^glog(y)} = y.

Eigenschappen van logaritmen:
Als 0 < g < 1 of g > 1 en als a > 0 en b > 0 geldt

^glog(a) + ^glog(b) = ^glog(a · b)
^glog(a) – ^glog(b) = ^glog( $\frac{a}{b}$ )
p · ^glog(a) = ^glog(a^p)

Verandering van grondtal:
Om met steeds hetzelfde grondtal te kunnen werken (de log-toets van je rekenmachine gebruikt altijd grondtal 10) moet je van grondtal kunnen veranderen.
Uit de eigenschappen van logaritmen kun je afleiden: ^glog(a) = ^plog(a) / ^plog(g).

Zo kun je logaritmen met je rekenmachine berekenen en/of als functie invoeren.

‡

Voorbeeld 1

De eigenschappen van logaritmen stellen je in staat met logaritmen te rekenen.
Bijvoorbeeld:

⁶log(24) + 2 · ⁶log(3) = ⁶log(24) + ⁶log(3²) = ⁶log(24 · 9) = ⁶log(216) = 3
²log(12) + ^0,5log(12) = ²log(12) + ²log(12) / ²log(0,5) = ²log(12) – ²log(12) = 0

Bereken nu zelf:

²log(72) – 2 · ²log(3) = ²log(72) – ²log(3²) = ²log(72/9) = ²log(8) = 3
²log(80) + ^0,5log(5) = ²log(80) + ²log(5) / ²log(0,5) = ²log(80) – ²log(5) =
= ²log(16) = 4
²log(7) · ⁷log(8) = ²log(7) · ²log(8) / ²log(7) = ²log(8) = 3
2^²log(7) = 7 (definitieformules)

‡

Voorbeeld 2

Los de vergelijking 2^t = 20.000 op m.b.v. de log-toets van je rekenmachine.

Antwoord

De log-toets op je GR werkt alleen met grondtal 10. Je schrijft daarom bij 10-logaritmen het grondtal niet meer op, gewoon log(2) betekent automatisch de 10-logaritme van 2. Je moet nu van grondtal 2 naar grondtal 10 wisselen.
Dit kun je op twee manieren aanpakken:

Ga uit van 2^t = 20.000 en neem aan beide zijde de 10-logaritme:
log(2^t) = log(20.000).
Met de eigenschappen van logaritmen wordt dit: t · log(2) = log(20.000).
Dus: t = log(20.000) / log(2) ≈ 14,2877.
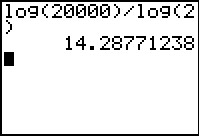De oplossing van 2^t = 20.000 is t = ²log(20.000).
Nu is ²log(20.000) = log(20.000) / log(2) ≈ 14,2877.

‡

Voorbeeld 3

Los de vergelijking ²log(x) = 3 algebraïsch op.

Antwoord

Bij het oplossen van zo'n vergelijking gebruik je de definitieformules.
Als je beide zijden een exponentiële functie met grondtal 2 toepast, krijg je:

2^²log(x) = 2³

En (zie definitieformules) dat betekent: x = 2³ = 8.

‡

Voorbeeld 4

Los de vergelijking log(x) + log(2x) = 3 algebraïsch op.

Antwoord

Bij het oplossen van dergelijke vergelijkingen gebruik je de eigenschappen van logaritmen:

log(x) + log(2x) = 3
	`darr` logaritmen optellen
log(x · 2x) = 3
	`darr` uitwerken
log(2x²) = 3
	`darr` exp. functie met grondtal 10 toepassen
2x² = 10³ = 1000
	`darr` delen door 2 en worteltrekken
x = $\sqrt{500}$ V x = – $\sqrt{500}$

Omdat je geen logaritme uit een negatief getal kunt trekken is er maar één oplossing mogelijk: x = $\sqrt{500}$ .

‡

Opgaven

In Voorbeeld 1 gaat het om de eigenschappen van logaritmen. Je kunt ze controleren door getallen in te vullen. Controleer:
1. ²log(16) + ²log(8) = ²log(128)
2. ²log(16) – 3 · ²log(2) = ²log(2)
3. ³log(3) + ³log(9) = ³log(27)

In Voorbeeld 2 zie je hoe de eigenschappen van logaritmen kunnen worden gebruikt om een vergelijking van het type `g^x = a` op te lossen. Er worden twee methodes gebruikt.
Los de volgende vergelijkingen op beide manieren op, geef benaderingen in vier decimalen nauwkeurig.
1. `3^x = 8100`
2. `(1/4)^x = 0,002`

Bekijk in Voorbeeld 3 hoe je een vergelijking kunt oplossen waarin een logaritme voor komt. Los nu zelf op:
1. ⁵`log(x) = 2`
2. ⁴`log(2x) = 0`
3. ^1/4`log(x^2) = -4`
4. ²`log(sqrt(x)) = 5`

Bestudeer in Voorbeeld 4 hoe je de eigenschappen van logaritmen gebruikt bij het exact oplossen van logaritmische vergelijkingen. Los nu zelf op:
1. `log(4x) + log(x) = 1`
2. `2 * log(x) - log(2x) = 2`

Verwerken

Gebruik de eigenschappen van logaritmen om te berekenen:
1. ¹⁰`log(5)` + ¹⁰`log(20)`
2. ⁵`log(100)` – ⁵`log(4)`
3. 2 · ⁶`log(3)` + ⁶`log(4)`
4. ^1/3`log(45)` – ^1/3`log(5)`

Ga na welke van de volgende logaritmen eenvoudig zonder rekenmachine te berekenen zijn. Geef van die opgaven het exacte antwoord. Bereken van de overige opgaven het antwoord tot op drie cijfers achter de komma. Gebruik hierbij de log-toets van de rekenmachine.
1. ⁵`log(625)`
2. ²`log(100)`
3. ^1/7`log(sqrt(7))`
4. ⁸`log(8000)`
5. ^1/3`log(50)`
6. ¹⁰`log(40)` + ¹⁰`log(25)`
7. ^1/3`log(0,0003)`

Een radioactieve stof vervalt volgens deze formule:
`N(t) = N(0) * 0,93^t`
`N` is de hoeveelheid in mg en `t` de tijd in jaren.
1. Hoeveel bedraagt de halveringstijd?
2. Een laboratorium heeft 400 g van deze stof. Bereken met behulp van de halveringstijd hoe lang het duurt voor dat deze hoeveelheid minder is geworden dan 50 g.
3. Bereken tot op een maand nauwkeurig hoe lang het duurt voor dat 50 g van deze stof minder is geworden dan 10 g.

Het radioactieve calcium-45 heeft een halveringstijd van 165 dagen.
1. Na hoeveel tijd is er van een willekeurige beginhoeveelheid calcium-45 nog 1/4 deel over?
2. Na hoeveel tijd is er van een willekeurige beginhoeveelheid calcium-45 nog 1/8 deel over?
3. In een laboratorium is 100 gram calcium-45 aanwezig. Schat met behulp van de antwoorden bij vraag a en b hoe lang het duurt tot deze hoeveelheid minder is geworden dan 15 gram.
4. Bereken het antwoord van c tot op een dag nauwkeurig.

Een hoeveelheid groeit exponentieel met groeipercentage `p` procent. Toon aan dat de verdubbelingstijd `T` gegeven wordt door
`T = (log(2))/(log(1 + p/100))`

Los de volgende vergelijkingen algebraïsch op. Geef daarna benaderingen in één decimaal nauwkeurig.
1. `10 * 5^x = 0,16`
2. ³`log(x^2) = 3`
3. `log(2x) - 2 * log(x) = 1`

Testen

Iemand koopt een huis voor € 200000,= en verwacht dat de waarde van het huis per jaar 10% zal stijgen.
1. Hoe lang duurt het voordat het huis € 300000,= waard is? Schrijf het antwoord als logaritme en bereken die logaritme tot op de maand nauwkeurig.
2. Hoe lang duurt het voordat de waarde van het huis twee keer zo groot is geworden?
3. Hoe lang duurt het voordat de waarde van het huis drie keer zo groot is geworden?
4. Hoe lang duurt het voordat de waarde van het huis zes keer zo groot is geworden? Laat zien hoe je dit kunt berekenen met behulp van de antwoorden bij b en c.
5. Hoe kun je het antwoord van vraag d in één keer berekenen?

Bij radioactieve stoffen wordt in plaats van het woord halveringstijd vaak het woord halfwaardetijd gebruikt. In een laboratorium bevindt zich 800 g van het radioactieve natrium-24. Deze stof heeft een halfwaardetijd van 15 uur.
1. Laat zien hoe lang het duurt tot er nog maar 100 g van het natrium-24 over is.
2. Hoeveel bedraagt de groeifactor per uur?
3. Bereken tot op een kwartier nauwkeurig hoe lang het duurt tot er van de 800 g natrium-24 nog maar 160 g over is.

Een suikerpatiënt moet zich een injectie met insuline toedienen op het moment dat er nog maar een derde deel van de vorige injectie insuline in zijn bloed zit. De hoeveelheid insuline in het bloed neemt per uur met 8% af.
Hoeveel tijd zit er tussen twee opeenvolgende injecties? Schrijf de oplossing als logaritme en geef een benadering in uren nauwkeurig.

Omstreeks 1650 groeide de wereldbevolking met een percentage van 0,3% per jaar. Schrijf de verdubbelingstijd als logaritme en geef een benadering in gehele jaren.

Los algebraïsch op:
1. `600 * 0,5^t = 20`
2. ⁵`log(1 - x) = 2`
3. ²`log(x) + `²`log(3x) = 5`