Logaritmen

Inleiding

Bij exponentiële verbanden zoals die bij bijvoorbeeld bacteriegroei optreden moet je soms vragen beantwoorden als: "Op welk tijdstip zijn er 100 miljoen bacteriën?"
Daarbij ontstaan vergelijkingen waarin exponentiële functies voorkomen. Die kun je nog niet algebraïsch oplossen, maar alleen oplossingen zoeken (vaak benaderen) met de grafische rekenmachine. In dit onderwerp leer hoe je logaritmen kunt gebruiken om dergelijke vergelijkingen wel algebraïsch op te lossen.

Je leert nu:

het begrip logaritme kennen;
logaritmen uit het hoofd berekenen waar dat kan;
logaritmen schatten.

Je kunt al:

werken met exponentiële functies, ook met de grafische rekenmachine;
werken met de begrippen macht, grondtal en exponent.

Verkennen

Voor het aantal bacteriën B in een petrischaaltje na t uur geldt B(t) = 600 · 2^t.

> Na hoeveel uur (in minuten nauwkeurig) zijn er 12 miljoen bacteriën?

Uitleg

Voor het aantal bacteriën B in een petrischaaltje na t uur geldt B(t) = 600 · 2^t.
Na hoeveel uur (in minuten nauwkeurig) zijn er 12 miljoen bacteriën?

Deze vraag kun je vertalen in het oplossen van de vergelijking 600 · 2^t = 12.000.000.
Ofwel: 2^t = 20.000.
Een dergelijke vergelijking los je op dit moment nog op met de grafische rekenmachine.
De oplossing is t ≈ 14,29.
De exacte oplossing noem je de logaritme van 20.000 voor het grondtal 2.
Dit schrijf je als t = ²log(20.000).

In het algemeen wordt de oplossing van een exponentiële vergelijking een logaritme genoemd.
Omdat exponentiële functies altijd stijgend (grondtal groter dan 1) of altijd dalend zijn (grondtal tussen 0 en 1) heeft een vergelijking als g^x = a precies één oplossing:
x = ^glog(a) als a > 0 (en anders geen).
Vooralsnog kun je deze oplossingen meestal alleen nog vinden door de intersect-functie van je GR te gebruiken.

‡

Opgaven

In de Uitleg werd de vergelijking `2^t = 20000` opgelost.
1. Bepaal zelf de oplossing van deze vergelijking in twee decimalen nauwkeurig.
2. Hoe schrijf je die oplossing als logaritme?
3. Na hoeveel uur heb je 6 miljoen bacteriën? Geef je oplossing als logaritme, maar ook benaderd in twee decimalen nauwkeurig.

Theorie

De oplossing van de vergelijking g^x = a heet de logaritme van a voor grondtal g.
Notatie: x = ^glog(a).

Omdat deze vergelijking alleen oplossingen heeft als 0 < g < 1 of g > 1 en als a > 0, bestaat ^glog(a) alleen onder deze voorwaarden.
Vooralsnog bepaal je ^glog(a) meestal met behulp van de intersect-functie van je grafische rekenmachine.

In het algemeen wordt als definitie van logaritme gebruikt:

uit g^x = y volgt x = ^glog(y);
uit x = ^glog(y) volgt g^x = y;

De uitdrukkingen x = ^glog(y) en g^x = y zijn volledig gelijkwaardig als 0 < g < 1 of g > 1 en als a > 0.
Je noemt de exponentiële functie en de logaritme met hetzelfde grondtal wel inverse bewerkingen, ze zijn elkaars terugrekenbewerkingen.

‡

Voorbeeld 1

Luchtschepen zijn gevuld met gas dat regelmatig aangevuld moet worden om voldoende draagvermogen te houden. Een luchtschip met een inhoud van 3000 m³ verliest elke 10 dagen ongeveer 2% van zijn gas. Als er minder dan 2400 m³ over is, kan het niet meer vliegen.
Hoeveel dagen nadat het geheel is gevuld is dit het geval?

Antwoord

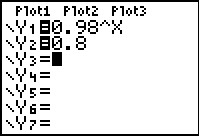De hoeveelheid gas in het luchtschip is G(t) = 3000 · 0,98^t met G in m³ en t in eenheden van 10 dagen.

De vraag kun je vertalen naar het oplossen van: 3000 · 0,98^t < 2400.
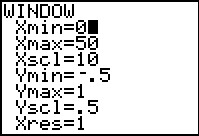De bijbehorende vergelijking is: 3000 · 0,98^t < 2400.
Na delen door 3000 levert dit op: 0,98^t < 0,8.
Met de intersect-functie van je GR vind je: t ≈ 11,04.
De oplossing van de vergelijking is daarom: t = ^0,98log(0,8) ≈ 11,04.

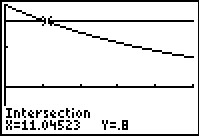
Het luchtschip kan 110 dagen vliegen zonder bijvullen. Op de 111de dag kan het niet meer vliegen.

‡

Voorbeeld 2

Soms kun je van een logaritme zelf de uitkomst bedenken:

²log(16) is de oplossing van 2^t = 16 = 2⁴.
Dus ²log(16) = 4.
³log( $\frac{1}{9}$ ) is de oplossing van 3^t = $\frac{1}{9}$ = 3^–2.
Dus ³log( $\frac{1}{9}$ ) = –2.

Bereken nu zelf:

³log(81) = 4, want 3⁴ = 81
¹⁰log(10.000) = 4, want 10⁴ = 10.000
¹⁰log(0,001) = –3, want 10^–3 = 0,001
²log( $\frac{1}{8}$ ) = –3, want 2^–3 = $\frac{1}{8}$
³log( $\frac{1}{9} \sqrt{3}$ ) = –1 $\frac{1}{2}$ , want 3^{–1 $\frac{1}{2}$} = $\frac{1}{9} \sqrt{3}$
^{^{$\frac{1}{2}$}}log(8) = –3, want ( $\frac{1}{2}$ )^–3 = 8

‡

Voorbeeld 3

Je kunt de grootte van een logaritme schatten m.b.v. machten van het grondtal:

²log(40) is een getal tussen 5 en 6, want 2⁵ = 32 en 2⁶ = 64.
¹⁰log(400) is een getal tussen 2 en 3, want 10² = 100 en 10³ = 1000.

Schat nu zelf:

³log(200) is een getal tussen 4 en 5, want 3⁴ = 81 en 3⁵ = 243
¹⁰log(200) is een getal tussen 2 en 3, want 10² = 100 en 10³ = 1000
¹⁰log(0,05) is een getal tussen –2 en –1, want 10^–2 = 0,01 en 10^–1 = 0,1
²log(0,4) is een getal tussen –2 en –1, want 2^–2 = 0,25 en 2^–1 = 0,5
^0,5log(20) is een getal tussen –5 en –4, want 0,5^–5 = 32 en 2^–4 = 16

‡

Opgaven

In Voorbeeld 1 gaat het om de hoeveelheid gas in een luchtschip. Je wilt nu weten na hoeveel dagen de beginhoeveelheid is verminderd tot 2800 m³.
1. Welke vergelijking moet je dan oplossen?
2. Je kunt die vergelijking eerst vereenvoudigen. Wat krijg je dan?
3. Schrijf nu de oplossing van de vergelijking op als logaritme. Geef ook een benadering van het antwoord in twee decimalen nauwkeurig.

Geef de oplossingen van de volgende vergelijkingen. Schrijf het antwoord als logaritme en bereken het (eventueel in drie decimalen nauwkeurig).
1. `2^x = 7`
2. `3^x = 81`
3. `(1/3)^x = 9`
4. `(1/3)^x = 0,01`
5. `10^x = 1000000`
6. `10^x = 0,001`
7. `0,001^x = 0,1`
8. `0,001^x = 100`

Bekijk in Voorbeeld 2 hoe je soms logaritmen exact kunt berekenen. Bereken de volgende logaritmen.
1. ⁵`log(125)`
2. ⁵`log(1/25)`
3. ⁴`log(64)`
4. ^1/4`log(64)`
5. ^1/3`log(1/81)`
6. ²`log(sqrt(2))`

Bestudeer in Voorbeeld 3 hoe je een logaritme kunt schatten. Geef van de volgende logaritmen steeds aan tussen welke twee opeenvolgende gehele getallen ze liggen.
1. ⁵`log(150)`
2. ¹⁰`log(758)`
3. ²`log(60)`
4. ²`log(1/7)`
5. ^1/2`log(20)`
6. ^1/3`log(1/5)`

Bereken de logaritmen uit de vorige opgave tot op één cijfer achter de komma nauwkeurig.

Schrijf de oplossing van de volgende vergelijkingen als logaritme. Geef daarna de oplossing tot op één cijfer achter de komma nauwkeurig.
1. `5 * 3^x = 3000`
2. `1,7^t = 525`
3. `572 * 0,6^t = 30`

Iemand zet op 1-1-2000 een kapitaal van € 10000,= op de bank tegen een vaste rente van 8% per jaar. In welke maand van welk jaar is dit kapitaal uitgegroeid tot € 15000,= als hij niets afhaalt of bijstort? Gebruik bij de berekening een logaritme.

Verwerken

Welke van de volgende logaritmen zijn eenvoudig zonder rekenmachine te berekenen? Bereken deze logaritmen. Bereken de overige logaritmen tot op één cijfer achter de komma.
1. ⁴`log(64)`
2. ⁴`log(400)`
3. ^1/3`log(60)`
4. ^1/3`log(81)`
5. ^1/3`log(1/81)`
6. ^0,1`log(1000000)`

Geef bij de volgende logaritmen steeds aan tussen welke twee opeenvolgende gehele getallen ze liggen.
1. ⁶`log(30)`
2. ³`log(70)`
3. ^1/2`log(10)`
4. ^1/3`log(0,01)`

Geef een benadering van de volgende logaritmen in drie decimalen nauwkeurig.
1. ^2,5`log(100)`
2. ^0,7`log(20)`
3. ^2,3`log(0,05)`
4. ^15,2`log(2,3)`

Schrijf de oplossing van de volgende vergelijkingen als logaritme. Geef daarna een benadering in één decimaal nauwkeurig.
1. `10 * 10^x = 0,1`
2. `0,5 * 2^x = 30`
3. `54 * 0,8^t = 27`

Een kolonie bacteriën groei exponentieel met groeifactor 2 per uur. Bereken in minuten nauwkeurig hoe lang het duurt voordat de kolonie zich heeft verdrievoudigd. Maak bij de berekening gebruik van logaritme.

Testen

Bereken de volgende logaritmen exact.
1. ²`log(sqrt(32))`
2. ^1/3`log(27)`

Geef bij de volgende logaritmen eerst aan tussen welke opeenvolgende gehele getallen ze liggen. Geef daarna een benadering in drie decimalen.
1. ²`log(513)`
2. ^0,4`log(25)`

Los de volgende vergelijkingen op. Schrijf de oplossing als logaritme en geef daarna een benadering in twee decimalen nauwkeurig.
1. `6 * 4^x = 35`
2. `1050 * 1,08^t = 1800`

In een tank zit 150 liter verontreinigde vloeistof. Deze vloeistof wordt verwijderd door spoelen met water. Hierdoor verdwijnt elke minuut 15% van de vloeistof. Men wil stoppen met spoelen als er minder dan 10 liter verontreinigde vloeistof over is. Bereken hoe lang men moet spoelen. Schrijf het antwoord als logaritme en geef een benadering van deze logaritme.