Lineaire modellen

Inleiding

Het komt regelmatig voor dat onderzoekers op grond van de gevonden resultaten een lineair verband tussen twee variabelen veronderstellen. Dat is bijvoorbeeld het geval als de meetpunten bij een verband tussen twee variabelen (vrijwel) op een rechte lijn liggen.
De kunst is dan om op grond van de meetgegevens een goede lineaire functie als model op te stellen. Hoe dat in zijn werk gaat wordt in dit onderdeel besproken.

Je leert nu:

• bij een lineair verband dat is gegeven door een aantal meetpunten een passende formule opstellen.

Je kunt al:

• grafieken tekenen bij (lineaire) functies;
• werken met lineaire verbanden en de bijbehorende hellingsgetallen (richtingscoëfficiënten).

Verkennen

De bevolking van een grote stad is de laatste jaren gestaag gegroeid. In de tabel vind je enkele gegevens:

> Maak bij deze tabel een grafiek.
> Je kunt een rechte lijn trekken die het verloop van de bevolkingsgroei van deze stad redelijk benaderd. Doe dat en probeer met behulp daarvan het aantal inwoners in 2010 en 2020 te voorspellen.

Uitleg

Als je bij de tabel van de bevolking van een grote stad een grafiek tekent, lijken de meetpunten ongeveer op een rechte lijn te liggen. Hoewel de groei niet precies lineair is, kun je hem goed benaderen door een lineair model. Je tekent dan een rechte lijn die zo goed mogelijk door de meetpunten gaat. Kies eerst een paar variabelen: N is het aantal inwoners (× 100.000) en t is de tijd in jaren vanaf 1950, dus t = 0 in 1950.

Een lijn die goed het verloop van de meetpunten beschrijft gaat door (20;5,3) en (50;9,8). (Ga dat zelf na door de punten te tekenen.)
Om een formule bij deze lijn op te stellen, zoek je eerst het hellingsgetal.
In 50 – 20 = 30 jaar tijd neemt N toe met 9,8 – 5,3 = 4,5.
Per jaar is dat een toename van `(4,5)/30 = 0,15`.
Dit is het hellingsgetal van de rechte lijn. De bijbehorende formule is dus N = 0,15t + b.
Om b te bepalen gebruik je dat de grafiek door (20;5,3) gaat, dus: 5,3 = 0,15 · 20 + b.
Dit betekent dat b = 2,3.
Het lineaire model heeft daarom als formule N = 0,15t + 2,3.

Hiermee kun je voorspellen hoe groot het aantal inwoners in 2010 en 2020 zal zijn.

‡

Opgaven

1. Bekijk het lineaire model dat in de Uitleg wordt opgesteld voor de bevolking van een grote stad.
   1. Ga na, dat door de meetpunten inderdaad ongeveer een rechte lijn door `(20;5,3)` en `(50;9,8)` gaat.
   2. Controleer of de gevonden formule bij de overige meetpunten ongeveer de juiste waarden oplevert.
   3. Voorspel het aantal inwoners van deze stad in 2010 en 2020.


2. Een cilindervormige kaars is 1,5 uur na het aansteken 25 cm lang en 4 uur na het aansteken nog 20 cm lang. Voor deze kaars kun je aannemen dat de lengte `L` (in cm) een lineaire functie van de brandtijd `t` (in uren) is.
   1. Bereken eerst het hellingsgetal van die lineaire functie. Welke betekenis heeft dit getal in de praktijk?
   2. Stel vervolgens het functievoorschrift `L(t)` op.
   3. Bereken met behulp van dat functievoorschrift na hoeveel uur deze kaars volledig is opgebrand.

Theorie

Soms wordt het verband tussen y en x gegeven door een tabel met meetpunten. Liggen die meetpunten (ongeveer) op een rechte lijn, dan kun je hierbij een lineair model opstellen. En daarbij hoort een lineaire functie van de vorm y = ax + b.

Gaat de rechte lijn door (10,210) en (30,300), dan bepaal je als volgt de lineaire formule:

• x neemt toe met 30 – 10 = 20;
• y neemt toe met 300 – 210 = 90;
• als x met 1 toeneemt, neemt y met `90/20 = 4,5` toe;
• het hellingsgetal (de richtingscoëfficiënt) van de lijn is 4,5;
• de gevraagde formule is y = 4,5x + b;
• (10,210) moet op de lijn liggen, dus 210 = 4,5 · 10 + b, dus b = 165.

De rechte lijn heeft als formule: y = 4,5x + 165.

‡

Voorbeeld 1

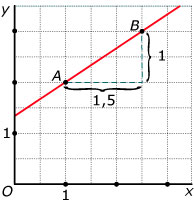
Hier zie je in een assenstelsel twee punten A en B getekend.
Tussen x en y bestaat een lineair verband.
Stel een formule op voor dit verband.

Antwoord

Lees af: A = (1,2) en B = (2,5;3).
Het gevraagde verband heeft de vorm y = ax + b. Door in de applet de waarden van a en b aan te passen kun je de formule maken.

Zo bereken je a en b:

• `a = (3 - 2)/(2,5 - 1) = 2/3`
• De formule wordt dan `y = 2/3 x + b`.
• A(1,2) invullen geeft: `2 = 2/3 * 1 + b` en dus `b = 1 1/3`.

De gevraagde formule is `y = 2/3 x + 1 1/3`.

‡

Voorbeeld 2

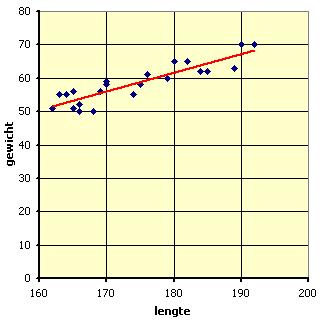
Van 22 scholieren in een 4 havo klas zijn lengte en gewicht gemeten en in Excel ingevoerd. Excel kan daar een zogenaamde trendlijn doorheen tekenen. Deze trendlijn geeft dan een verband tussen lengte L (in cm) en gewicht G (in kg).
Hier is gekozen voor een lineair verband. Stel daarbij een passende formule op.

Antwoord

De formule krijgt de vorm: G = a · L + b.
De lijn gaat ongeveer door (160,50) en (190,67).

• `a = (67 - 50)/(190 - 160) ~~ 0,57`.
• Dus krijg je G = 0,57L + b.
• Punt (160,50) invullen geeft 50 = 0,57 · 160 + b, dus b ≈ –41,2.

De gevraagde formule is G = 0,57L – 41,2.

‡

Voorbeeld 3

Je kunt de formule voor het lineaire verband in Voorbeeld 1 ook zo opstellen.

De punten A = (1,2) en B = (2,5;3) moeten aan de vergelijking `y=ax+b` voldoen:

• A(1,2) geeft: 2 = a + b
• B(2,5;3) geeft: 3 = 2,5a = b

Trek je beide vergelijkingen van elkaar af, dan vind je: 1 = 1,5a.
Dus `a = 2/3`.
En (na invullen): `b = 4/3`.
De vergelijking van de lijn is `y = 2/3 x + 1 1/3`.

‡

Opgaven

3. Bekijk in Voorbeeld 1 hoe je de vergelijking opstelt van een lijn door twee gegeven punten.
   Lijn `l` gaat door de punten `(-3, 2)` en `(17, 10)`. Stel een vergelijking van `l` op.
   


4. In Voorbeeld 2 zie je hoe bij een verzameling meetpunten een lineair model wordt opgesteld door een zo goed mogelijk passende lijn te trekken en twee punten op die lijn af te lezen uit de figuur.
   1. Stel dat je afleest dat de rechte lijn gaat door `(170,56)` en `(195,70)`. Welke vergelijking krijgt de lijn dan?
   2. Bepaal met de formule die je bij a hebt gevonden hoe zwaar een scholier van 1,60 m uit deze groep zou moeten zijn.


5. In Voorbeeld 3 tref je een andere manier aan om de vergelijking van een lijn door twee gegeven punten op te stellen.
   Lijn `l` gaat door de punten `(-3, 2)` en `(17, 10)`. Stel een vergelijking van `l` op door deze methode toe te passen.
   


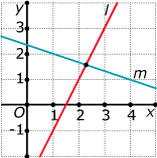6. Je ziet hier twee lijnen `l` en `m`.
   1. Stel van elk van deze lijnen een vergelijking op.
   2. Bereken vervolgens exact het snijpunt van beide lijnen.


7. Dit zijn twee bijzondere situaties:
   1. Stel een vergelijking op van de lijn door `(2,1)` en `(12,1)`.
   2. Stel een vergelijking op van de lijn door `(2,1)` en `(2,10)`.

Verwerken

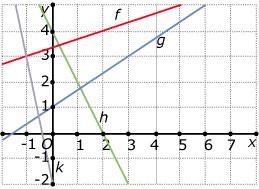
8. In dit assenstelsel staan vier grafieken van lineaire functies. Stel bij elk van deze functies het functievoorschrift op.
   
   
   
   


9. Stel een vergelijking op van de rechte lijn `l` die wordt beschreven door:
   1. `l` gaat door de punten `(30,68)` en `(34,56)`.
   2. `l` gaat door de punten `(-2,100)` en `(-3,100)`.
   3. `l` heeft richtingscoëfficiënt 0,5 en gaat door `(-2,4)`.
   4. `l` is de `x`-as.
   5. `l` is de `y`-as.


10. Bereken algebraïsch het snijpunt van de lijnen `l` door `P(13,8)` en `Q(43,48)` en `m` door `R(43,28)` en `T(23,38)`.
    


11. Voor gassen geldt de wet van Gay-Lussac. Het volume `V` (in m³) van een bepaalde hoeveelheid gas bij een bepaalde druk hangt af van de temperatuur `t` (in °C). Er geldt:
    `(V(t))/(t + 273) = (V(0))/273`
    waain `-273`°C het absolute nulpunt is en `V(0)` het volume bij `0`°C is.
    1. Herschrijf deze formule tot: `V(t) = V(0) * (1 + 1/273 t)`.
    2. Leg uit dat er sprake is van een lineair model. Welke aanname moet je doen wil dat model geldig zijn? Welk domein moet je kiezen?
    3. Neem `V(0) = 1` m³ en breng de bijbehorende grafiek in beeld. Schrijf de geschikte vensterinstellingen op.
    4. Welk volume heeft dit gas bij kamertemperatuur?
    5. Bij welke temperatuur is het volume 1,5 keer zo groot geworden?


12. Bij een éénparige beweging beweegt een voorwerp met een constante snelheid langs een rechte baan. In de natuurkunde wordt dat aangegeven met de formule:
    `s(t) = s(0) + v * t`
    waarin `s(t)` de afgelegde weg (in m) na `t` seconden is.
    1. Wat stelt `s(0)` voor? Wat stelt `v` voor?
    2. Neem `s(0) = 0` en `v = 20` m/s voor een bepaald voorwerp. Breng de bijbehorende grafiek van `s(t)` in beeld.
    3. Een tweede voorwerp heeft 400 m voorsprong en beweegt langs dezelfde baan met een snelheid van 15 m/s. Geef de formule die bij de beweging van dit voorwerp past en breng de bijbehorende grafiek in beeld.
    4. Bereken op welk tijdstip het eerste voorwerp het tweede heeft ingehaald.


13. Bij een eenparig versnelde beweging beweegt een voorwerp met een constante versnelling a (in m/s²) langs een rechte baan. In de natuurkunde wordt dat aangegeven door:
    `v(t) = v(0) + a * t`
    waarin `v(t)` de snelheid (in m/s) na `t` seconden is.
    1. Wat stelt `v(0)` voor?
    2. Een voorwerp vertrekt met een beginsnelheid van 40 m/s. De constante versnelling is ongeveer 10 m/s². Na hoeveel seconden beweegt het met een snelheid van 350 m/s?
    3. Om een voorwerp met een massa `m` van 1000 kg dat met een constante snelheid van 40 m/s beweegt tot stilstand te brengen, wordt een bepaalde remkracht `F` (in newton) uitgeoefend. Het voorwerp moet binnen 8 seconden tot stilstand komen. Er geldt `F=m*a` met `F` in newton, `m` in kg en `a` de versnelling in m/s². Bereken de grootte van de remkracht `F`.

Testen

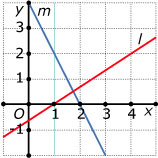14. In deze figuur staan twee lijnen `l` en `m`. Stel van elk van deze lijnen een vergelijking op.
    Bereken vervolgens algebraïsch het snijpunt van beide lijnen.
    


15. Stel een vergelijking op van de rechte lijn die beschreven wordt door:
    1. De lijn gaat door de punten `(40,32)` en `(34,56)`.
    2. De lijn heeft richtingscoëfficiënt `-2` en gaat door `(-2,4)`.
    3. De lijn gaat door `(3,2)` en is evenwijdig aan de `y`-as.


16. De uitzetting van een metalen staaf verloopt lineair met de temperatuur `T` als deze gelijkmatig wordt verhit. In de natuurkunde wordt daarvoor de formule:
    `l(T) = l(0) * (1 + alpha · T)`
    gebruikt, waarin `l(T)` de lengte (in m) van de staaf na het verhitten tot `T`°C is. De constante `alpha` heet de lineaire uitzettingscoëfficiënt.
    1. Wat stelt `l(0)` voor?
    2. Voor ijzer geldt: `alpha = 9 * 10^(-6)`.
       Ga uit van een ijzeren staaf met `l(0) = 0,5` m.
       Hoe lang is deze staaf op kamertemperatuur (20°C)?
       Tot hoeveel graden Celsius moet je hem verhitten om de staaf 1 mm langer dan `l(0)` te laten worden?
    3. Voor koper geldt: `alpha = 1,7 * 10^(-5)`.
       Een staaf koper van 50 cm bij 20°C wordt verhit tot 100°C. Bereken de lengte van deze staaf bij 100°C.