Lineaire verbanden in het algemeen

Inleiding

Lineaire functies zijn voorbeelden van veel algemenere lineaire verbanden met twee variabelen. Een eenvoudig voorbeeld is het verband tussen lengte l en breedte b als de omtrek van een rechthoek is gegeven. Maar er zijn meer situaties te bedenken waarin tussen twee variabelen een lineair verband bestaat...

Je leert nu:

een lineair verband tussen twee variabelen herkennen;
bij een in woorden beschreven lineair verband een passende formule opstellen;
grafieken tekenen bij lineaire verbanden in het algemeen;
lineaire formule herschrijven naar lineaire functies.

Je kunt al:

grafieken tekenen bij lineaire functies;
werken met lineaire functies.

Verkennen

De omtrek van rechthoek OAPB is 30.
De lengte van deze rechthoek is l, de breedte is b.

> Welke formule geldt voor het verband tussen `l` en `b`?
> Waarom is de bijbehorende grafiek in een `l,b`-assenstelsel een rechte lijn?

Uitleg

Een formule als 2x + 3y = 6 is een lineaire vergelijking met twee variabelen. De grafiek bij zo’n lineaire vergelijking is een rechte lijn, want je kunt de vergelijking herschijven naar een lineaire functie. Dat gaat zo:

2x + 3y = 6                 _{aan beide kanten 2x aftrekken}
       3y = –2x + 6        _{aan beide kanten delen door 3}
         y = –`2/3x+2`

Op de rechte lijn liggen alle punten (x,y) die voldoen aan 2x + 3y = 6 en ook aan
`y = 2/3 x + 2`.
Om die rechte lijn te tekenen, is het niet nodig om de formule te herschrijven. Je kunt ook even enkele punten van de lijn bepalen:

Als x = 0, dan is 3y = 6 en dus y = 2. Het punt (0,2) ligt op de lijn.
Als x = 1, dan is `2 + 3y = 6` en dus `y=4/3`. Het punt `(1,4/3)` ligt op de lijn.
Als y = 0, dan is 2x = 6 en dus x = 3. Het punt (3, 0) ligt op de lijn.

Omdat de grafiek bij een lineaire vergelijking een rechte lijn is, heb je genoeg aan twee punten om hem te tekenen. Vaak neem je daarvoor de punten met x = 0 of y = 0.

‡

Opgaven

Bekijk de Uitleg.
Een ander voorbeeld van een lineaire vergelijking met twee variabelen is: `3x - 4y = 12`.
1. Teken de lijn met deze vergelijking door eerst de snijpunten met de beide assen te berekenen.
2. Herschrijf de vergelijking tot een lineaire functie. Geef in je grafiek het begingetal en het hellingsgetal van deze lineaire functie aan.
3. Bereken met behulp van het functievoorschrift opnieuw het snijpunt met de `x`-as.

Theorie

Een vergelijking van de vorm ax + by = c beschrijft een lineair verband met twee variabelen. De grafiek ervan is een rechte lijn. Je kunt die grafiek tekenen door punten van deze lijn op te zoeken. Vaak doe je dat door x = 0 te kiezen en de bijbehorende waarde voor y uit te rekenen en door y = 0 te kiezen en de bijbehorende waarde voor x uit te rekenen.

Lineaire vergelijkingen met twee variabelen zoals ax + by = c kun je herschrijven naar een lineaire functie als b ≠ 0.
Zo is 2x + 3y = 6 te schrijven als `y = -2/3 x + 2`.
En dit is een lineaire functie met begingetal 2 en hellingsgetal `-2/3`.

Bijzondere gevallen:

a = 0: de vergelijking heeft dan de vorm by = c en is te herschrijven tot `y=c/b`. Dit is een lineaire functie met hellingsgetal 0.
b = 0: de vergelijking de vorm ax = c en is te herschrijven tot `x=c/a`. Dit is geen lineaire functie; er is geen hellingsgetal. De grafiek is een lijn evenwijdig aan de y-as.

‡

Voorbeeld 1

Een muziekvoorstelling trok veel bezoekers. Een kinderkaartje kostte € 2,50 en een kaartje voor volwassenen kostte € 4,50. In totaal is er voor € 1110,00 aan inkomsten door de kaartverkoop.
Hoeveel kinderen en hoeveel volwassenen zaten er in de zaal?

Antwoord

Echt beantwoorden kun je deze vraag niet, er zijn meerdere combinaties mogelijk.

Is het aantal kinderen in de zaal x en het aantal volwassenen in de zaal y, dan geldt: 2,50x + 4,50y = 1110.
Dit is een lineair verband tussen x en y.
Je kunt de formule herschrijven tot: y = (1110 – 2,50x)/4,50.
Maak je nu met de GR een tabel dan kun je gemakkelijk alle mogelijke combinaties waarbij x en y gehele getallen zijn vaststellen.
Bijvoorbeeld: x = 3 en y = 245 of x = 12 en y = 240, enzovoorts..., tot en met x = 444 en y = 0.

‡

Voorbeeld 2

Een muziekvoorstelling trok veel bezoekers. Een kinderkaartje kostte € 2,50 en een kaartje voor volwassenen kostte € 4,50. In totaal is er voor € 1110,00 aan inkomsten door de kaartverkoop.
x is het aantal kinderen en y het aantal volwassenen in de zaal.
Maak een grafiek bij het verband tussen beide variabelen.

Antwoord

Bij het verband tussen beide variabelen hoort de lineaire vergelijking
2,50x + 4,50y = 1110.
Je kunt dit ook schrijven als 5x + 9y = 2220.
Er zijn twee manieren om hierbij een grafiek te tekenen.

Omdat je weet dat bij een lineair verband een rechte lijn als grafiek hoort, heb je aan twee punten (x,y) die aan de vergelijking voldoen genoeg. Je vindt die snel door eerst x = 0 en vervolgens y = 0 te kiezen: (0,2220/9) en (444,0).
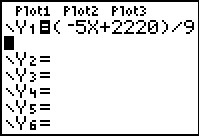
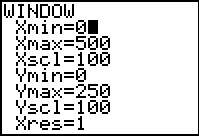
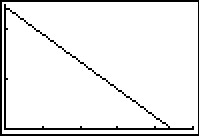
Je herschrijft de vergelijking tot: y = (–5x + 2220)/9 en gebruikt de grafische rekenmachine om de grafiek te tekenen. Het wordt een rechte lijn met richtingscoëfficiënt –5/9 en door (0,2220/9).

‡

Voorbeeld 3

Bij een lineair verband hoort in het algemeen de vergelijking ax + by = c. Bij

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Lineaire verbanden > Lineaire verbanden > Voorbeeld 3

vind je een applet waarin je a, b en c kunt variëren.
Bekijk wat er gebeurt als je deze getallen verandert.
Let vooral op de bijzondere gevallen:

a = 0: de grafiek is een lijn die evenwijdig aan de x-as;
b = 0: de grafiek is een lijn die evenwijdig aan de y-as;
c = 0: de grafiek gaat door O(0,0).

En wat gebeurt er met de grafiek als a = b, of a = –b?

‡

Opgaven

Bekijk Voorbeeld 1.
Je ziet daarin een lineair verband tussen de variabelen `x` en `y` gegeven door `2,5x + 4,5y = 1110`.
1. Laat zien dat je deze formule kunt herschrijven tot `y = -5/9 x + 246 2/3`.
2. Kunnen er 300 kinderen bij de voorstelling aanwezig zijn geweest? Licht je antwoord toe.

In Voorbeeld 2 zie je hoe je een grafiek maakt bij de vergelijking `2,5x + 4,5y = 1110`.
1. Waarom kun je in dit geval de grafiek het beste tekenen door eerst de snijpunten met de assen te berekenen?
2. Maak zelf de grafiek op je grafische rekenmachine.
3. Er waren 185 volwassenen bij de voorstelling. Hoeveel kinderen waren er?

Je ziet hier vier keer de vergelijking van een lijn. Om die lijn te tekenen kun je eerst de snijpunten met de assen opzoeken en hem dan daar doorheen trekken. Je kunt ook eerst de vergelijking herschrijven tot een lineaire functie en dan begingetal en richtingscoëfficiënt gebruiken voor het tekenen van de lijn. Gebruik bij de onderstaande lijnen elk van deze methoden in ieder geval één keer.
1. `5x + 4y = 20`
2. `5x - 4y = 20`
3. `2x + y = 10`
4. `x - 2y = 10`

Je komt in Voorbeeld 3 ook horizontale en verticale lijnen tegen.
1. Hoe ziet de vergelijking van een verticale lijn er uit?
2. Waarom kun je bij een verticale lijn geen functievoorschrift opstellen?

De algemene vorm van een lineaire vergelijking met twee variabelen is: `ax + by = c`.
1. Herschrijf deze vergelijking tot een functievoorschrift van de vorm `y = ...`.
2. Waarom moet bij a gelden dat `a =! 0`?
3. Welk bijzondere geval krijg je als `a = 0` terwijl `b =! 0` en `c =! 0`?
4. Welk bijzondere geval krijg je als `b = 0` terwijl `a =! 0` en `c =! 0`?
5. Welk bijzondere geval krijg je als `c = 0` terwijl `a =! 0` en `b =! 0`?

Welke van deze vergelijkingen kun je herschrijven tot een lineaire functie? Bepaal in dat geval de richtingscoëfficiënt van de bijbehorende lijn en breng de grafiek in beeld met je grafische rekenmachine.
1. `2x - 3y = 12`
2. `2x - 3 = 12`
3. `x = -2y + 6`
4. `4y - 6 = 0`

Verwerken

Teken de lijnen met de volgende vergelijkingen en bepaal de richtingscoëfficiënt van de lijn (indien mogelijk):
1. `-2x + 3y = 6`
2. `6x - 2y = 24`
3. `y = 2x + 1`
4. `4x + y = 10`
5. `20x = 45`
6. `y + 2 = 0`

Gegeven zijn de lijnen `l`: `2x - 4y = -3` en `m`: `5x + 4y = 8`.
1. Bereken van beide lijnen algebraïsch de snijpunten met de coördinaatassen.
2. Breng beide lijnen op je grafische rekenmachine in beeld.
3. Bepaal de coördinaten van hun snijpunt in twee decimalen nauwkeurig.

Stel je voor dat je een groep van 180 personen van drinken wilt voorzien. Je koopt daarvoor literpakken appelsap en sinaasappelsap. Je hebt 90 pakken nodig en je beschikt over € 100,= om de frisdrank te kopen. Appelsap kost € 0,90 per literpak en sinaasappelsap € 1,05 per literpak. Noem het aantal pakken appelsap `a` en het aantal pakken sinaasappelsap `s`.
1. Aan welke twee vergelijkingen moeten deze variabelen voldoen?
2. Breng de bijbehorende grafieken in beeld op je grafische rekenmachine.
3. Beide variabelen kunnen alleen gehele waarden aannemen. Welke oplossing vind je als je zo min mogelijk geld wilt overhouden?

Deze puzzel wordt toegeschreven aan Euklides (ongeveer 300 v.Chr.). Los hem op.

Een ezel en een muildier sjokken voort, beladen met allemaal even zware zakken. De ezel zucht onder zijn last, waarop het muildier tegen zijn lotgenoot zegt: "Wat kreun en jammer je toch! Tweemaal zoveel zou ik dragen als jij, als je mij één zak van jouw zou geven, terwijl we evenveel zouden dragen als je er één van mij nam."
Hoeveel zakken draagt ieder dier?

Testen

Teken de lijnen met de volgende vergelijkingen en bereken als dat mogelijk is de richtingscoëfficiënt:
1. `5x + 2y = 10`
2. `-2x + 5y = 7`
3. `x = 4`
4. `4 - 2y = 0`

In een bak zitten 1000 pakjes. In een aantal van die pakjes zit een cadeautje van € 9,=, in de overige zit een cadeautje ter waarde van € 1,=. Het totale bedrag aan cadeautjes in de bak is € 3000,=.
De vraag is: Hoeveel pakjes met een cadeautje van € 9,= zitten er in de bak?
1. Stel twee lineaire vergelijkingen op om dit probleem op te lossen
2. Breng de lijnen die bij deze vergelijkingen horen in beeld op je grafische rekenmachine.
3. Bepaal de oplossing van het probleem.
4. Waarom is in dit geval een grafische oplossing heel nauwkeurig?