
Lineaire functies

Inleiding
De kosten voor het verbruik van leidingwater bedragen een vast bedrag per m3, dat verschilt per regio.
In een bepaalde regio zou je dus zeggen dat de kosten voor het verbruik van leidingwater recht evenredig zijn met de hoeveelheid die je verbruikt. Maar dat is niet zo...
Je betaalt namelijk ook nog een soort van abonnementskosten, het vastrecht.
Als het vastrecht € 65,00 per jaar is en je betaalt 1,25 per m3, dan past hierbij een formule zoals K = 1,25 · a + 65 als a het jaarverbruik (in m3) en K de jaarlijkse kosten zijn. Er bestaat een lineair verband tussen K en a.
Je leert nu:
- een lineair verband tussen twee variabelen herkennen;
- bij een in woorden beschreven lineair verband een passende formule opstellen;
- de grafiek van een lineair verband tekenen en daarbij het begrip hellingsgetal (richtingscoëfficiënt) gebruiken.
Je kunt al:
- grafieken tekenen bij functies;
- werken met eenvoudige lineaire verbanden.
Verkennen
De kosten voor het verbruik van leidingwater bedragen in een bepaalde regio € 1,25 per m3 en het vastrecht is € 65,00 per jaar.
Hierbij past de formule K = 1,25 · a + 65 waarin a het jaarverbruik (in m3) en K de jaarlijkse kosten zijn.
> Breng de grafiek van K als functie van a goed in beeld.
> In Nederland wordt per persoon gemiddeld ongeveer 124 L water per dag gebruikt. Zijn er jaren dat een huishouden in deze regio meer dan 1000 euro aan water kwijt is?
Uitleg
De kosten voor het verbruik van leidingwater bedragen in een bepaalde regio € 1,25 per m3 en het vastrecht is € 65,00 per jaar.
Hierbij past de formule K = 1,25 · a + 65 waarin a het jaarverbruik (in m3) en K de jaarlijkse kosten zijn.
Zelfs als je geen water verbruikt betaal je toch € 65 per jaar voor de aansluiting.
Dus bij a = 0 hoort K = 65.
 Vervolgens zorgt elke extra m3 water die je verbruikt voor een toename van K met 1,25. Dit betekent dat elke toename van a met 1 een stijging van K met 1,25 tot gevolg heeft. De grafiek wordt daarom een rechte lijn en het getal 1,25 bepaalt hoe steil die rechte lijn loopt.
Vervolgens zorgt elke extra m3 water die je verbruikt voor een toename van K met 1,25. Dit betekent dat elke toename van a met 1 een stijging van K met 1,25 tot gevolg heeft. De grafiek wordt daarom een rechte lijn en het getal 1,25 bepaalt hoe steil die rechte lijn loopt.
En dus zeg je dat er een lineair verband tussen a en K bestaat.
("linea recta" is "volgens een rechte lijn")
Het getal 1,25 noem je wel het hellingsgetal van de lijn.
In Nederland wordt per persoon gemiddeld ongeveer 124 L water per dag gebruikt. Dit betekent 45260 L per persoon per jaar. Als een gemiddeld huishouden uit 4 personen bestaat, dan is dit 181.040 L per jaar voor zo'n huishouden.
Omdat dit ongeveer 181,04 m3 per jaar is bedragen de kosten voor een gemiddeld huishouden in deze regio € 291,30 per jaar.
‡
Opgaven
-
Bekijk de Uitleg.
In een andere regio zijn de jaarlijkse kosten `K` voor het verbruik van water € 1,20 per m3 met een vastrecht van € 70,00 per jaar.
-
Welke formule geldt voor `K` als functie van `a`, als `a` het jaarverbruik in m3 voorstelt?
-
Met hoeveel neemt `K` toe als `a` met 1 m3 toeneemt?
-
Hoeveel betaal je in deze regio als je geen water verbruikt?
-
Een huishouden verbruikt in een bepaald jaar 195 m3 water. Hoeveel moeten ze dat jaar betalen?
-
Bij welke vensterinstellingen krijg je de grafiek van `K` zo in beeld dat voor een verbruik tot 300 m3 de kosten zijn af te lezen uit de grafiek?
-
Voor welke waarde van `a` geldt: `K(a) = 250`? Licht het antwoord toe.
Theorie
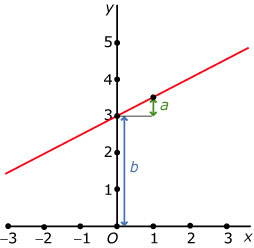
Als y een lineaire functie is van x heeft de bijbehorende formule de vorm y = a · x + b, waarin
- a het hellingsgetal, dus de toe(af)name per stap van 1 is;
- b het begingetal, de uitkomst bij x = 0 is.
De grafiek bij zo'n lineair verband is een rechte lijn door (0, b).
Als je de waarde van x daarna met 1 ophoogt, neem de uitkomst met a toe of af.
Het hellingsgetal a heet ook wel de richtingscoëfficiënt, want dit getal bepaalt de richting van de grafiek.
‡
Voorbeeld 1
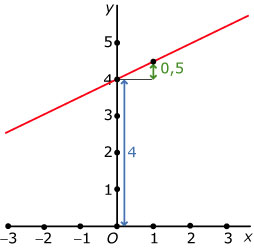
Hoe teken je de grafiek bij een lineair verband gegeven door de formule y = 0,5x + 4?
Antwoord
Er zijn twee manieren om dit te doen:
-
Methode I:
Het begingetal is 4 dus de grafiek "start" in (0,4).
Het hellingsgetal is 0,5, dus vanaf het punt (0,4) ga je elke keer dat de x-waarde met 1 toeneemt 0,5 omhoog om een nieuw punt te vinden. Dit betekent dat de grafiek ook door (1;4,5), (2,5), (3;5,5), enzovoorts gaat.
-
Methode II:
Zoek twee punten van de grafiek.
Bij x = 0 hoort y = 4.
Bij x = 6 hoort y = 0,5 · 6 + 4 = 7.
Trek de lijn door deze twee punten.
‡
Voorbeeld 2
Als een loodgieter bij een particulier een reparatie moet uitvoeren, vraagt hij voorrijkosten, een uurtarief en materiaalkosten. een bepaalde loodgieter vraagt € 35,00 aan voorrijkosten en het uurtarief is € 28,50.
Als je niet op de materiaalkosten let, dan zijn de arbeidskosten A in euro alleen afhankelijk van de gewerkte tijd t in uren.
Welke formule kun je daarvoor opstellen?
Antwoord
Deze loodgieter kost als je hem belt om te komen in ieder geval 35 euro.
Elk gewerkt uur kost nog eens 28,50 euro, dus t uur werken kost t · 28,50 euro.
In totaal zijn de arbeidskosten: A = 35 + 28,50 · t.
‡
Voorbeeld 3
De temperatuur hangt (onder de juiste omstandigheden) lineair af van de hoogte boven de zeespiegel. Zeker bij een wandeling in de bergen of een ballontochtje kun je dat goed merken. Een vuistregel is dat elke 100 m stijging een temperatuursdaling van 0,6°C betekent. Stel je voor dat het op 0 m hoogte 24°C is.
Welke formule kun je opstellen voor de temperatuur (in °C) afhankelijk van de hoogte (in m)?
Bepaal met je grafische rekenmachine op welke hoogte de temperatuur voor het eerst onder 0°C komt.
Antwoord
De temperatuursdaling per meter is 0,0/100 = 0,006°C.
De formule is daarom T = 24 – 0,006h als h de hoogte in m en T de temperatuur in °C is.
Maak vervolgens met je rekenmachine een geschikte grafiek, zorg er voor dat het nulpunt in beeld komt!
Bepaal (met je rekenmachine of door berekening) dat de temperatuur 0°C is als h = 4000 m.
‡
Opgaven
-
Bekijk Voorbeeld 1.
Gegeven is de functie `f(x) = -0,2x + 6`.
-
Waaraan kun je al meteen zien dat de grafiek van `f` dalend is?
-
Teken de grafiek van `f` en geef behalve het hellingsgetal ook de snijpunten met de assen erin aan.
-
Bereken algebraïsch het snijpunt van de grafiek van `f` met de `x`-as.
-
De lineaire functie `g` heeft hetzelfde hellingsgetal, maar de grafiek gaat door `(10, 9)`.
Bepaal het functievoorschrift van `g`.
-
Elke lineaire functie heeft een voorschrift van de vorm `y = ax + b`.
-
Neem `a = 2` en `b = 3` en breng de grafiek van deze functie in beeld. Ga na of de grafiek door `(99, 200)` gaat.
-
Neem `a = 2`. Bekijk de grafieken van deze lineaire functies voor verschillende waarden van `b`.
Voor welke waarde van `b` gaat deze functie door `(99, 200)`?
-
Neem `b = 3`. Bekijk de grafieken van deze lineaire functies voor verschillende waarden van `a`.
Voor welke waarde van `a` gaat deze functie door `(99, 200)`?
-
Voor een rit met een taxi betaal je (bijvoorbeeld) € 3,50 voorrijkosten en nog eens € 1,20 per gereden km. Hierbij past een lineaire functie voor de ritprijs `R` afhankelijk van het aantal gereden km `a`.
In Voorbeeld 2 zie je hoe je in zo'n situatie een formule voor deze lineaire functie kunt opstellen.
-
Stel een formule op voor `R` als functie van `a`.
-
Welk getal is de richtingscoëfficiënt van `R(a)`?
-
Waarom heeft het nulpunt van `R(a)` hier geen betekenis?
-
Hoeveel betaal je voor een rit van 16 km?
-
Hoeveel km heb je gereden als je € 31,10 moet betalen?
-
Bestudeer Voorbeeld 3.
-
Licht toe hoe je aan de formule `T = 24 - 0,006h` komt.
-
Bereken algebraïsch het nulpunt van de grafiek van `T`.
-
Schrijf op welke vensterinstellingen je gebruikt de grafiek van `T` goed in beeld te krijgen.
-
Hoe hoog is de temperatuur op de top van Mount Everest (8884 m boven de zeespiegel)?
Verwerken
-
Fietser 1 gaat met een constante snelheid van 20 km/h van A naar B. Fietser 2 gaat
met een constante snelheid van 25 km/h van B naar A. De afstand tussen A en B is
voor beide fietsers 150 km. `a` is de afstand tot A en `t` is de tijd in uren.
-
Teken in een `a,t`-assenstelsel van beide fietstochten de grafiek.
-
Stel voor beide fietsers een passende formule op voor het verband tussen `a` en `t`.
-
Na hoeveel tijd passeren beide fietsers elkaar? Licht je antwoord toe.
-
Bereken van de volgende lineaire functies de snijpunten met de assen. Teken vervolgens
de bijbehorende grafieken door gebruik te maken van begingetal en hellingsgetal.
Controleer zo de berekende snijpunten.
-
`h(t) = 3t - 5`
-
`f(x) = x - 4`
-
`g(x) = -0,5x + 4`
-
`k(x) = -2(x + 3)`
-
Gegeven is de functie `y_1 = -4 + 5x`.
-
Teken de grafiek van deze functie en geef het begingetal en het hellingsgetal in die grafiek aan.
-
De grafiek van `y_1` wordt 10 eenheden langs de `y`-as omhoog geschoven.
Bepaal het functievoorschrift van de grafiek van `y_2` die daardoor ontstaat.
-
De grafiek van `y_1` wordt gespiegeld in de `y`-as.
Bepaal het functievoorschrift van de grafiek van `y_3` die daardoor ontstaat.
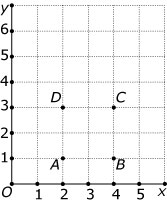 Je ziet hier een assenstelsel met een vierkant `ABCD` erin. In dit assenstelsel gaat de
grafiek van een lineaire functie door het punt `(1,5)`.
Je ziet hier een assenstelsel met een vierkant `ABCD` erin. In dit assenstelsel gaat de
grafiek van een lineaire functie door het punt `(1,5)`.
-
Leg uit waarom de bijbehorende formule `y = ax + 5 - a` moet zijn.
-
Voor welke waarden van `a` heeft de grafiek van deze functie geen punten met het vierkant gemeen?
-
Gegeven zijn de functies `f(x) = 4 - 0,5x` en `g(x) = 2x - 1`.
-
Bereken algebraïsch de snijpunten van deze functies met de beide coördinaatassen.
-
Bereken algebraïsch het snijpunt van beide grafieken.
-
De Elfstedentocht is een schaatstocht langs de elf Friese steden. Het laatste stuk is een
vrijwel rechte tocht van Dokkum naar Leeuwarden met een lengte van 26 km.
Een deelnemer komt na 7 uur schaatsten in Dokkum aan. Hij schaatst dit laatste stuk
voor de wind met een vrijwel constante snelheid. Na drie kwartier is hij in Leeuwarden
en heeft hij ongeveer 200 km afgelegd.
-
Met welke snelheid heeft hij het laatste deel van de tocht gereden?
-
Stel je voor dat `t` de tijd in uren is, `t = 0` op het moment dat deze deelnemer aan de Elfstedentocht begint.
Verder is `a` de afgelegde afstand. Welk functievoorschrift `a(t)` geldt er voor het laatste deel van zijn tocht?
-
Deze deelnemer is tegelijk met mij begonnen aan de schaatstocht. Ik kom echter 2 uur na hem pas in Dokkum aan.
Ook ik schaats met een constante snelheid het laatste stuk, maar doe er een uur over.
Welke formule geldt voor mijn tocht van Dokkum naar Leeuwarden?
Testen
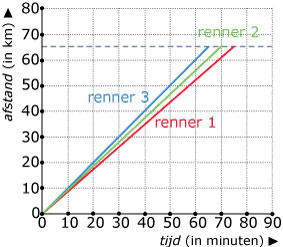
-
In de Tour de France wordt een aantal keren
een tijdrit gereden. In deze grafieken vind
je gegevens over een tijdrit van 65 km.
-
Welke renner heeft de tijdrit gewonnen? Waar zie je dat aan?
-
Waarom kunnen deze grafieken nooit het werkelijke verloop van deze tijdrit correct beschrijven?
-
Bereken van iedere renner de gemiddelde snelheid.
-
Schrijf voor elke grafiek een passende formule op.
-
Gegeven is de lineaire functie `f` met voorschrift: `f(x) = 7x + 10`.
-
Bereken exact de snijpunten van de grafiek van `f` met de `x`-as en de `y`-as.
-
De grafiek van `f` wordt 3 eenheden in de `y`-richting omlaag geschoven.
Welk functievoorschrift hoort bij de nieuwe grafiek die daardoor ontstaat?
-
De grafiek van `f` wordt gedraaid om het punt `(0,10)`.
De nieuwe grafiek gaat door `(10,15)`.
Welk functievoorschrift past bij die nieuwe grafiek?
-
De grafiek van `f` wordt gedraaid om het punt `(0,10)` en vervolgens 2 eenheden omhoog geschoven.
De nieuwe grafiek gaat door `(10,0)`. Welk functievoorschrift past bij die nieuwe grafiek?
 Vervolgens zorgt elke extra m3 water die je verbruikt voor een toename van K met 1,25. Dit betekent dat elke toename van a met 1 een stijging van K met 1,25 tot gevolg heeft. De grafiek wordt daarom een rechte lijn en het getal 1,25 bepaalt hoe steil die rechte lijn loopt.
Vervolgens zorgt elke extra m3 water die je verbruikt voor een toename van K met 1,25. Dit betekent dat elke toename van a met 1 een stijging van K met 1,25 tot gevolg heeft. De grafiek wordt daarom een rechte lijn en het getal 1,25 bepaalt hoe steil die rechte lijn loopt.



 Je ziet hier een assenstelsel met een vierkant `ABCD` erin. In dit assenstelsel gaat de
grafiek van een lineaire functie door het punt `(1,5)`.
Je ziet hier een assenstelsel met een vierkant `ABCD` erin. In dit assenstelsel gaat de
grafiek van een lineaire functie door het punt `(1,5)`.
