
Totaalbeeld
Samenvatten
Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Functies en grafieken. Een eigen samenvatting maken is nuttig.
Begrippenlijst:
21: functie — invoerwaarde — functiewaarde — functievoorschrift
22: domein — bereik — nulwaarden/nulpunten — extremen/toppen
23: asymptoten — karakteristieken (nulpunten, toppen, asymptoten)
24: transformaties — verschuiven (translatie) — lijnvermenigvuldiging
25: ongelijkheid
Activiteitenlijst:
21: functies herkennen — de notaties bij het functiebegrip gebruiken
22: het domein en het bereik van een functie bepalen — de intervalnotatie gebruiken
23: asymptoten bepalen — karakteristieken van een functie bepalen
24: transformaties herkennen en uitvoeren
25: ongelijkheden oplossen
Achtergronden
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Totaalbeeld > Achtergronden
Testen
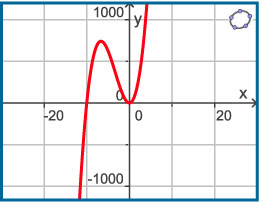 Gegeven zijn de functies `f(x) = 5x^2(x + 20)` en `g(x) = 50x^2`.
De grafiek van `f` zie je hiernaast.
Gegeven zijn de functies `f(x) = 5x^2(x + 20)` en `g(x) = 50x^2`.
De grafiek van `f` zie je hiernaast.
-
Bereken algebraïsch de nulpunten van `f` en breng de grafiek in beeld.
Pas de vensterinstellingen zo aan, dat je hetzelfde beeld krijgt als in de gegeven grafiek.
Zet nu ook de grafiek van `g` er bij.
-
Bereken de snijpunten van de grafieken van `f` en `g`.
-
Los op: `f(x) < g(x)`.
-
Bereken bij deze functies eerst de nulpunten. Bepaal vervolgens domein en bereik.
-
`f(x) = x^2(x^2 - 400)`
-
`g(x) = sqrt(20-x) - 40`
-
Gegeven is de functie `y(x) = 4 - 1/(x^2)`.
-
Welke asymptoten heeft de grafiek van deze functie?
-
Schrijf domein en bereik op.
-
Los op: `y >= 2`. Geef benaderingen in twee decimalen nauwkeurig.
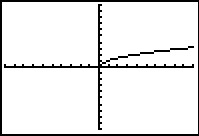 Hieronder zie je vier grafieken die zijn ontstaan door op de grafiek van `f(x) = sqrt(x)` één of meer transformaties toe te passen. Steeds zijn de standaardinstellingen van het GR-venster gebruikt.
Hieronder zie je vier grafieken die zijn ontstaan door op de grafiek van `f(x) = sqrt(x)` één of meer transformaties toe te passen. Steeds zijn de standaardinstellingen van het GR-venster gebruikt.
Schrijf bij elke grafiek het juiste functievoorschrift op.
a. 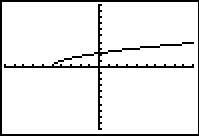 b.
b. 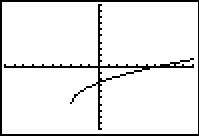 c.
c. 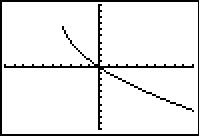 d.
d. 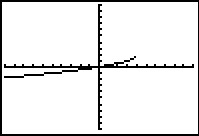
-
Gegeven is de functie `f` met `f(x) = 0,25(x - 10)^4 - 16`.
-
Door welke transformaties kan de grafiek van `f` ontstaan uit die van `y = x^4`?
-
Bepaal de top en de nulpunten van de grafiek van `f`.
-
Los algebraïsch op: `f(x) < 10`.
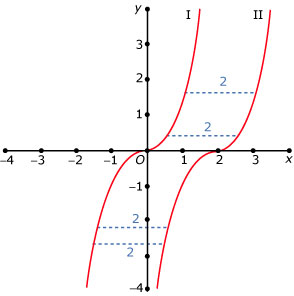 In de figuur zie je de grafieken I en II.
In de figuur zie je de grafieken I en II.
I is de grafiek van `y = x^3`.
Grafiek II ligt rechts van I, zodanig dat alle horizontale verbindingslijnstukken van I en II de lengte 2 hebben.
-
Geef een bij grafiek II passend functievoorschrift.
-
De verticale verbindingslijnstukken van I en II variëren in lengte.
Bereken algebraïsch de waarden van `x` waarvoor die lengte 26 is.
-
Bereken de kortste lengte van zo’n verticaal verbindingslijnstuk.
Toepassen
-
Een leuke manier om het werken met transformaties te oefenen is het tekenen van “smiley’s” met je grafische rekenmachine. Bekijk hoe je dat doet.
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Totaalbeeld > Toepassingen
Maak zelf een smiley en laat een medeleerling bedenken welke formules je hebt gebruikt. Doe daarna het omgekeerde.
-
Door een technische storing in de airconditioning van een groot gebouw neemt het zuurstofgehalte in de lucht tijdelijk af. Lees hierover meer in…
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Totaalbeeld > Toepassingen
De technische staf heeft het verloop van het zuurstofgehalte beschreven met de formule: `Z(t) = 200(1 - (10)/(t+10) + (100)/((t+10)^2))`.
Hierin is `t` de tijd in minuten gerekend vanaf het moment dat de storing begon. Verder is `Z` het aantal cm3 zuurstof per liter lucht op het tijdstip `t`. Op `t = 0` is het zuurstofgehalte normaal.
-
Bereken `Z(0)`. Schets de grafiek van `Z(t)` voor `0 <= t <= 100`.
-
Op welk tijdstip is het zuurstofgehalte minimaal?
-
De medische staf vindt een zuurstofgehalte van 80% van het normale niveau, nog juist toelaatbaar.
Bereken gedurende hoeveel minuten het zuurstofgehalte ontoelaatbaar laag is.
-
Van een rechthoekig stuk karton van 12 cm bij 20 cm kun je een bakje maken. Je knipt dan de vier hoeken even ver in, zoals je in de figuren kunt zien.
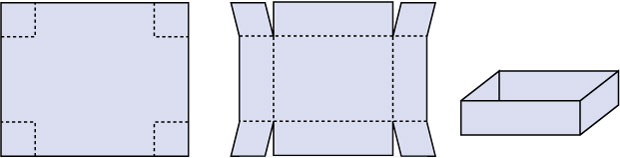
Als je er op dezelfde wijze een deksel bij maakt, krijg je een doosje waarvan de inhoud `I` wordt bepaald door de afmetingen van het bakje.
-
Noem de lengte en de breedte van het ingeknipte stukje `x`. Stel een formule op voor `I(x)`.
-
Bepaal het domein en het bereik van `I(x)`.
-
Hoe ver moet je het karton inknippen om een maximale inhoud te krijgen?
Examenopgaven
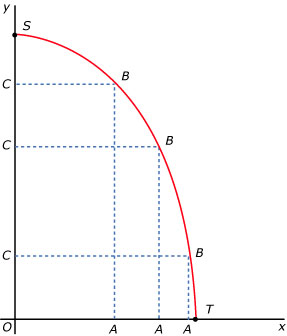 Gegeven is de functie `f(x) = sqrt(1-2x)`.
Gegeven is de functie `f(x) = sqrt(1-2x)`.
`T` en `S` zijn de snijpunten van de grafiek van `f` met de `x`-as en de `y`-as.
-
Bereken de coördinaten van `T` en `S`.
-
Schrijf domein en bereik van `f` op.
-
In de figuur zie je hoe punt `B` de grafiek van `f` doorloopt tussen `T` en `S`.
De punten `A` en `C` zijn steeds de projecties van `B` op respectievelijk de `x`-as en de `y`-as.
Als `B` niet samenvalt met `T` of `C` is `OABC` een rechthoek. Die rechthoek verandert voortdurend van vorm.
Er is één plaats van `B` waarbij `OABC` een vierkant is. Bereken de coördinaten van deze plaats.
-
Als `B` van `T` naar `S` beweegt over de grafiek van `f`, neemt de oppervlakte van `OABC` eerst toe en later weer af.
Iemand heeft het vermoeden dat de oppervlakte van `OABC` maximaal is wanneer `OABC` een vierkant is.
Onderzoek of dit vermoeden juist is.
(bron: examen wiskunde B havo 1991, tweede tijdvak)
-
Gegeven is de functie `f(x) = (136x^2)/(x^4+16)` voor `-10 <= x <= 10`.
-
Breng de grafiek van `f` zo in beeld dat de hoogste en laagste functiewaarden zichtbaar zijn. Bepaal het bereik van `f`.
-
Los algebraïsch op: `f(x) >= 8`.
-
De grafiek van de functie `g(x) = f(x) + c` raakt de lijn `y = 10`.
Bepaal met behulp van je grafiek voor welke waarden van `c` dit het geval is.
(bron: examen wiskunde B havo 1989, eerste tijdvak)

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Totaalbeeld > Achtergronden  Gegeven zijn de functies `f(x) = 5x^2(x + 20)` en `g(x) = 50x^2`.
De grafiek van `f` zie je hiernaast.
Gegeven zijn de functies `f(x) = 5x^2(x + 20)` en `g(x) = 50x^2`.
De grafiek van `f` zie je hiernaast.
 In de figuur zie je de grafieken I en II.
In de figuur zie je de grafieken I en II.![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Totaalbeeld > Toepassingen
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Totaalbeeld > Toepassingen

 Gegeven is de functie `f(x) = sqrt(1-2x)`.
Gegeven is de functie `f(x) = sqrt(1-2x)`.