
Transformaties
Inleiding
Veel functies ontstaan vanuit een eenvoudige basisfunctie door in het voorschrift een getal op te tellen en/of met een getal te vermenigvuldigen. De grafieken van dergelijke functies lijken dan sterk op die van de basisfunctie. En de karakteristieken van die grafieken zijn uit die van de basisfunctie af te leiden.
Zo zijn alle functies van de vorm y = ax + b af te leiden uit de basisfunctie y = x. En dus hebben ze dezelfde grafiek, namelijk een rechte lijn.
Bij dit onderdeel heb je bij enkele opgaven een computer nodig!
Je leert nu:
- in een functievoorschrift herkennen of de functie is ontstaan uit een eenvoudige basisfunctie door optellen of vermenigvuldigen met een getal;
- grafieken van functies die door transformatie ontstaan uit een basisfunctie afleiden uit de grafiek van die basisfunctie.
Je kunt al:
- de karakteristieken van een functie bepalen en zo de grafiek goed in beeld krijgen;
- het domein en het bereik van een functie opschrijven;
- de belangrijkste basisfuncties.
Verkennen
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Inleiding
Werk met de applet. Bedenk steeds welke parameter `a`, `b`, `c` en/of `d` je moet aanpassen. Experimenteer tot je de regelmaat kunt formuleren!

Theorie
Ga uit van een basisfunctie y = f(x).
-
De grafiek van y = f(x) + 2 ontstaat door de grafiek van f in de y-richting 2 eenheden te verschuiven.
-
De grafiek van y = f(x + 2) ontstaat door de grafiek van f in de x-richting –2 eenheden te verschuiven.
Dit zijn twee transformaties van een grafiek.
Door het optellen van een getal in het functievoorschrift verschuift de grafiek.
In plaats van verschuiving spreek je ook wel van translatie.
De karakteristieken van de getransformeerde functies kun je afleiden uit die van de basisfunctie.
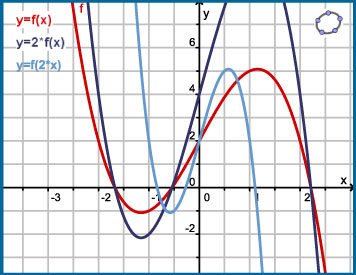
Ga uit van een basisfunctie y = f(x).
-
De grafiek van y = 2 · f(x) ontstaat door de grafiek van f in de y-richting met 2 te vermenigvuldigen.
-
De grafiek van y = f(2 · x) ontstaat door de grafiek van f in de x-richting met 1/2 te vermenigvuldigen.
Ook dit zijn twee transformaties van een grafiek.
Door het vermenigvuldigen van een getal in het functievoorschrift wordt de grafiek vermenigvuldigd vanuit een as.
Dit noem je lijnvermenigvuldiging t.o.v. een as.
De karakteristieken van de getransformeerde functies kun je afleiden uit die van de basisfunctie.
‡
Voorbeeld 1
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Voorbeeld 1
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Voorbeeld 1
‡
Voorbeeld 2
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Voorbeeld 2
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Voorbeeld 2
‡
Voorbeeld 3
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Voorbeeld 3
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Voorbeeld 3
‡
Voorbeeld 4
Je maakt gebruik van het herkennen van de transformaties als je een grafiek op je grafische rekenmachine in beeld wilt brengen. Je moet dan goed nadenken over de instellingen van het venster.
Daarbij is het nuttig om te zien dat een bepaalde functie door transformatie kan ontstaan uit een veel eenvoudiger basisfunctie. Zeker als je van die basisfunctie alle karakteristieken weet.
Hoe breng je de grafiek van f(x) = 200 – 5(x – 30)2 goed in beeld?
Antwoord
Je herkent dan de functie als f(x) = –5(x – 30)2 + 200 met als bijbehorende basisfunctie y = x2.
Die basisfunctie heeft als grafiek een dalparabool met top (0, 0).
De grafiek van f ontstaat uit die van y = x2 door:
- een verschuiving van +30 in de x-richting;
- een vermenigvuldiging van –5 in de y-richting;
- een verschuiving van +200 in de y-richting.
De top van de grafiek van f is daarom (30, 200) en de grafiek is een dalparabool.
De grafiek van y = x2 is goed in beeld met venster [–10,10] × [–10,10].
Op dit venster kun je ook de beschreven transformaties toepassen.
De grafiek van f is daarom goed in beeld op [20,40] × [150,250].
‡
Opgaven
-
Werk in Voorbeeld 1 met de applet.
Gegeven is de grafiek van functie `f` met een onbekend voorschrift `f(x)`.
-
Maak de grafiek van `g_1(x) = f(x + 2)`. Hoe ontstaat de grafiek van `g_1` uit die van `f`?
-
Maak de grafiek van `g_1(x) = f(x)+2`. Hoe ontstaat de grafiek van `g_1` uit die van `f`?
Neem nu aan dat `f(x) = x^3 - 4x`.
-
Schrijf het voorschrift van `g_1` op.
-
Schrijf het voorschrift van `g_2` op.
-
Oefen dit met andere functies `g_1` en `g_2`.
In de Theorie, pagina 2 en in Voorbeeld 2 kun je zien hoe de grafieken van
`g_1(x) = f(c_1 * x)` en `g_2(x) = c_2 * f(x)` kunnen ontstaan door die van `y = f(x)` te vermenigvuldigen in horizontale of verticale richting.
-
Werk in Voorbeeld 2 met de applet.
Gegeven is de grafiek van functie `f` met een onbekend voorschrift `f(x)`.
-
Maak de grafiek van `g_1(x) = f(2 * x)`. Hoe ontstaat de grafiek van `g_1` uit die van `f`?
-
Maak de grafiek van `g_2(x) = 2 * f(x)`. Hoe ontstaat de grafiek van `g_2` uit die van `f`?
Neem nu aan dat `f(x) = x^3 - 4x`.
-
Schrijf het voorschrift van `g_1` op.
-
Schrijf het voorschrift van `g_2` op.
-
Oefen dit met andere functies `g_1` en `g_2`.
-
In de applet van Voorbeeld 3 kun je alle vier de transformaties toepassen op functie `f`. Geef bij elk van de volgende functies aan welke transformaties je moet toepassen om de grafiek uit die van `f` te laten ontstaan. (Let op de volgorde!)
-
`g(x) = 2 * f(x) + 3`
-
`h(x) = f(x - 4) + 2`
-
`k(x) = 2 - f(x)`
-
`l(x) = f(3x) + 2`
-
`m(x) = 2 * f(3(x - 1)) + 4`
-
Schrijf het functievoorschrift op van `g` als de grafiek uit die van `f` ontstaat door
-
in de `y`-richting met `-2` te vermenigvuldigen en dan 1 omhoog te schuiven;
-
in de `x`-richting met 2 te vermenigvuldigen en dan `-3` in de `y`-richting te verschuiven;
-
in de `x`-richting 4 te verschuiven en dan in de `y`-richting `-2` te verschuiven;
-
in de `x`-richting met 0,5 te vermenigvuldigen en dan in de `x`-richting 4 te verschuiven;
-
in de `x`-richting 4 te verschuiven en dan in de `x`-richting met 0,5 te vermenigvuldigen en tenslotte in de `y`-richting `-2` te verschuiven.
-
Werk nu met je grafische rekenmachine. Ga uit van de basisfunctie `y_1 = x^2`.
-
Breng de grafiek van `y_1` in beeld met de standaardinstellingen van het venster.
-
Breng nu de grafieken van de volgende vier functies in beeld:
- `y_2 = x^2 + 2`
- `y_3 = (x + 2)^2`
- `y_4 = 2 * x^2`
- `y_5 = (2 * x)^2`
Onderzoek bij elk van die grafieken welke transformatie er moet worden toegepast op de grafiek van `y_1` om die grafiek te krijgen.
-
De grafiek van `y_6 = 0,5(x - 3)^2 + 4` ontstaat ook door transformatie van die van `y_1`.
Welke transformaties moeten er achtereenvolgens worden toegepast?
-
Door welke transformaties ontstaat de grafiek van `y_7 = -x^2` uit die van `y_1`?
-
Welke algemene vorm heeft het voorschrift van een functie die door transformaties ontstaat uit die van `y_1 = x^2`?
-
Hoe kun je door gebruik te maken van transformaties de top van de parabool `y = -2(x - 12)^2 + 315` bepalen?
-
Gegeven is de functie `f(x) = 0,25(x - 5)^4 - 10`.
De grafiek van deze functie kan door transformaties ontstaan uit die van de bijbehorende basisfunctie.
-
Welke basisfunctie is dat?
-
Welke transformaties moeten er dan achtereenvolgens worden toegepast?
-
Bepaal nu het minimum van de grafiek van de gegeven functie. Voor welke waarde van `x` treedt dit minimum op?
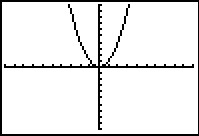 Je ziet hier de grafiek van `y_1 = x^2` in de standaardinstellingen van het venster van je rekenmachine.
Bekijk de zes grafieken in de standaardinstellingen van het venster van de grafische rekenmachine. Ze zijn allemaal ontstaan uit transformatie van de grafiek van `y_1`. Geef bij elke grafiek aan welke transformatie er is toegepast. Schrijf ook het juiste functievoorschrift op.
Je ziet hier de grafiek van `y_1 = x^2` in de standaardinstellingen van het venster van je rekenmachine.
Bekijk de zes grafieken in de standaardinstellingen van het venster van de grafische rekenmachine. Ze zijn allemaal ontstaan uit transformatie van de grafiek van `y_1`. Geef bij elke grafiek aan welke transformatie er is toegepast. Schrijf ook het juiste functievoorschrift op.
a. 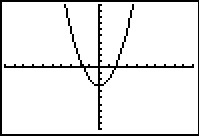 b.
b. 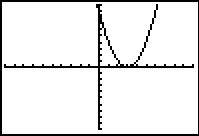 c.
c. 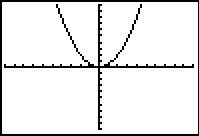
d. 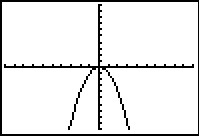 e.
e. 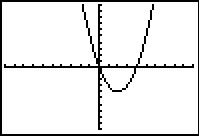 f.
f. 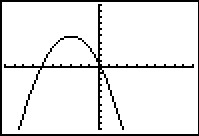
-
In de vorige opgave heb je gewerkt met transformaties van de functie `y_1 = x^2`.
Je kunt zo ook werken met andere basisfuncties zoals `y = x^3`, `y = sqrt(x)` en `y = 1/x`:
- Vanuit een gegeven formule de bijbehorende basisfunctie herkennen en voorspellen (door transformaties op te schrijven) waar de grafiek ligt.
- Vanuit een gegeven grafiek bedenken welke transformaties er op de bijbehorende basisfunctie zijn toegepast en dan het functievoorschrift opschrijven.
Oefen dit met één van je medeleerlingen.
-
Bekijk de Toepassing van het werken met transformaties.
De grafiek van de functie `f` met `f(x) = (x - 20)^2 + 200` komt met de standaardinstellingen van het venster op je grafische rekenmachine niet in beeld.
Leg uit, hoe je door het toepassen van transformaties de vensterinstellingen in één klap zo kunt maken, dat die grafiek wel goed in beeld komt.
Verwerken
-
Ga uit van de basisfunctie `f(x) = sqrt(x)`. De grafieken van de onderstaande functies kun je door transformatie van deze basisfunctie krijgen. Geef bij elk van die functies aan welke transformaties dat zijn.
-
`y_2 = 0,5 * f(x)`
-
`y_3 = f(x - 4) + 2`
-
`y_4 = 2 - f(x)`
-
`y_5 = f(3x) + 2`
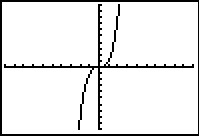 Hier zie je vijf keer het venster van je grafische rekenmachine in de basisinstellingen. De grafiek hiernaast is die van `y1 = x^3`. De overige grafieken zijn door transformatie van die grafiek ontstaan. Geef bij elke functie het juiste voorschrift.
Hier zie je vijf keer het venster van je grafische rekenmachine in de basisinstellingen. De grafiek hiernaast is die van `y1 = x^3`. De overige grafieken zijn door transformatie van die grafiek ontstaan. Geef bij elke functie het juiste voorschrift.
a. 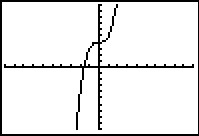 b.
b. 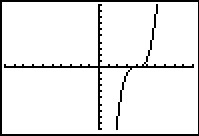 c.
c. 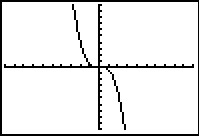 d.
d. 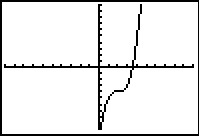
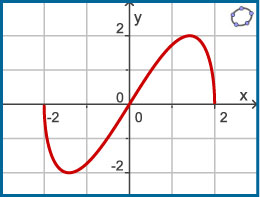 Hier zie je de grafiek van `y_1 = f(x)`. Neem hem over op een roosterblad.
Teken de grafieken van de volgende functies. Schrijf erbij welke transformaties je toepast.
Hier zie je de grafiek van `y_1 = f(x)`. Neem hem over op een roosterblad.
Teken de grafieken van de volgende functies. Schrijf erbij welke transformaties je toepast.
-
`y_2 = f(x - 2)`
-
`y_3 = -2 * f(x)`
-
`y_4 = f(x)-2`
-
`y_5 = f(2x)-1`
-
Een weggeslingerde kogel beschrijft ten opzichte van een xy-assenstelsel de volgende baan: `y = -0,02 (x - 10)^2 + 4`.
Het moment van loslaten ligt op `y = 2` m. Dit is bij `x = 0`.
`y` en `x` zijn beide in meter uitgedrukt.
-
Leg uit met behulp van transformaties hoe je de volledige baan van de kogel op de grafische rekenmachine in beeld kunt krijgen.
-
Bereken hoe ver deze kogelstoter met zijn kogel komt.
-
Na hoeveel meter is de kogel weer even hoog als op het moment van loslaten?
Testen
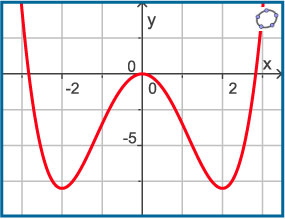 Hier zie je de grafiek van een functie `y_1 = f(x)`.
Welke transformaties moet je toepassen om de grafiek te krijgen van de volgende functies?
Hier zie je de grafiek van een functie `y_1 = f(x)`.
Welke transformaties moet je toepassen om de grafiek te krijgen van de volgende functies?
-
`y_2 = f(x - 3)`
-
`y_3 = 0,5 * f(x) + 1`
-
`y_4 = f(3x)`
-
Om de grafiek van `f(x) = 10 sqrt(x) + 50` goed in beeld te krijgen op je grafische rekenmachine, moet je weten hoe deze ontstaat door transformatie van de bijbehorende basisfunctie.
-
Welke basisfunctie is dat?
-
Welke transformaties moet je op de grafiek van de basisfunctie toepassen?
-
Schrijf op bij welke vensterinstellingen de grafiek van `f` goed in beeld komt.
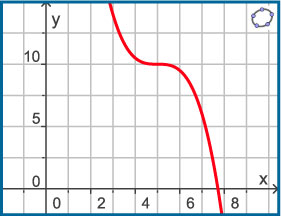 Je ziet hier de grafiek van een functie `g` die door transformatie is ontstaan uit de grafiek van `f(x) = x^3`.
De grafiek van `g` gaat door `(7,6)`. Schrijf het bijpassende functievoorschrift op.
Je ziet hier de grafiek van een functie `g` die door transformatie is ontstaan uit de grafiek van `f(x) = x^3`.
De grafiek van `g` gaat door `(7,6)`. Schrijf het bijpassende functievoorschrift op.

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Inleiding


![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Voorbeeld 1
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Voorbeeld 1
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Voorbeeld 2
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Voorbeeld 2
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Voorbeeld 3
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Transformaties > Voorbeeld 3
 Hier zie je de grafiek van `y_1 = f(x)`. Neem hem over op een roosterblad.
Teken de grafieken van de volgende functies. Schrijf erbij welke transformaties je toepast.
Hier zie je de grafiek van `y_1 = f(x)`. Neem hem over op een roosterblad.
Teken de grafieken van de volgende functies. Schrijf erbij welke transformaties je toepast.
 Hier zie je de grafiek van een functie `y_1 = f(x)`.
Welke transformaties moet je toepassen om de grafiek te krijgen van de volgende functies?
Hier zie je de grafiek van een functie `y_1 = f(x)`.
Welke transformaties moet je toepassen om de grafiek te krijgen van de volgende functies?
 Je ziet hier de grafiek van een functie `g` die door transformatie is ontstaan uit de grafiek van `f(x) = x^3`.
De grafiek van `g` gaat door `(7,6)`. Schrijf het bijpassende functievoorschrift op.
Je ziet hier de grafiek van een functie `g` die door transformatie is ontstaan uit de grafiek van `f(x) = x^3`.
De grafiek van `g` gaat door `(7,6)`. Schrijf het bijpassende functievoorschrift op.