Karakteristieken

Inleiding

Om functies te kunnen bestuderen is het vaak handig als je bijbehorende grafieken kunt bekijken. In veel gevallen, ook vaak in praktische situaties, zijn die grafieken niet eenvoudig goed in beeld te krijgen. Je wilt immers alle bijzonderheden kunnen zien! Pas dan kun je toppen bepalen en het bereik vaststellen.
De kenmerkende eigenschappen van een grafiek (nulpunten, toppen, enz.) noem je karakteristieken.

Je leert nu:

• wat asymptoten zijn;
• op welke manier je de karakteristieken van een functie kunt bepalen;
• extremen berekenen met behulp van de grafische rekenmachine.

Je kunt al:

• het begrip functie en de bijbehorende notaties gebruiken;
• grafieken en tabellen van functies maken (ook met de grafische rekenmachine);
• het domein en het bereik van een functie opschrijven.

Verkennen

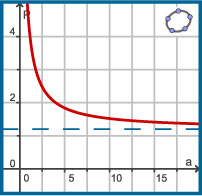
De huurprijs van een kopieerapparaat bedraagt € 250,00 per maand. Het maken van een kopie kost € 0,06. Op school staat zo’n apparaat speciaal voor gebruik door leerlingen. De leerlingen betalen € 0,10 per kopie.

> Geef een formule voor de prijs per kopie (P) als functie van het aantal kopieën (a).
> Welke waarde benaderen de functiewaarden als a heel groot wordt?
> En als a dicht bij 0 komt?

Uitleg

Voor een rit in een taxi betaal je:

• voorrijkosten € 3,20
• per gereden kilometer € 1,20

De prijs P per gereden km hangt af van het aantal gereden km a.
Er geldt: `P=1,20+(3,20)/a`.

De grafiek van deze functie heeft geen nulpunten, of extremen, maar wel geldt:

• Als a (het aantal gereden kilometers) heel groot wordt, benaderen de functiewaarden het getal 1,20. Je ziet dat als je een tabel bij de functie maakt.
  Dit betekent dat de grafiek steeds dichter bij de lijn P = 1,20 komt te liggen. Deze lijn heet de horizontale asymptoot van de grafiek van P.
• Als a dicht bij 0 komt, worden de functiewaarden steeds groter: P(0,1) = 33,20; P(0,01) = 321,20; P(0,001) = 3201,20; P(0,0001) = 32001,20; etc.
  Het getal 0 zelf mag je echter niet voor a invullen: delen door 0 levert geen reëel getal op.
  Dit betekent dat de grafiek steeds dichter bij de lijn a = 0 (de verticale as) komt te liggen. Dit is de verticale asymptoot van de grafiek van P.

Als je de grafiek van de functie tekent, zorg je er voor dat ook dit soort karakteristieke gedrag zichtbaar wordt, net als nulpunten en toppen.

‡

Opgaven

1. Bekijk de Uitleg en vooral het begrip asymptoot.
   Van een bepaald type kopieerapparaat worden de maandelijkse kosten per kopie gegeven door `K(a) = 200/a + 0,075`. Hierin is `a` het aantal kopieën per maand en `K` zijn de kosten in euro.
   1. Bereken de kosten per kopie als er 10000 kopieën per maand met deze machine worden gemaakt.
   2. Welke waarde benaderen de kosten per kopie als het aantal kopieën heel erg groot is?
   3. Welke horizontale asymptoot heeft de grafiek van `K`?
   4. Als er een bepaalde maand geen kopieën worden gemaakt, kun je niet spreken van de kosten per kopie. Het minimale aantal kopieën waarbij dit nog wel kan is 1. Hoeveel bedragen de kosten per kopie maximaal?

Theorie

Bij functies komen regelmatig asymptoten voor. Dat zijn lijnen waar de grafiek steeds dichter naast loopt naarmate je verder van de oorsprong van het assenstelsel komt.
Vooral een verticale asymptoot kun je vaak goed in het functievoorschrift herkennen: een invoerwaarde waarbij je door 0 moet delen veroorzaakt vaak zo’n asymptoot.
Een horizontale asymptoot ontstaat als de functiewaarden een vast getal naderen naarmate de invoerwaarden heel groot of heel klein (erg negatief) worden.

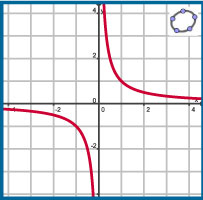
De functie f met voorschrift `f(x)=1/x` is het prototype van een functie met asymptoten. Je ziet er hiernaast de grafiek van. Deze grafiek heeft:

• als horizontale asymptoot de lijn y = 0, want voor grote en kleine (erg negatieve) waarden van x naderen de functiewaarden steeds dichter naar 0;
• als verticale asymptoot de lijn x = 0, want dit getal heeft geen functiewaarde (je kunt niet door 0 delen) en vlak in de buurt van 0 worden de functiewaarden heel groot of heel klein (erg negatief).

Het domein van f schrijf je als D_f = `(:larr,0:) uu (0,rarr:)`.
En het bereik is B_f  = `(:larr,0:) uu (0,rarr:)`.
Het teken `uu` betekent dat het gaat om alle getallen van de twee intervallen samen.

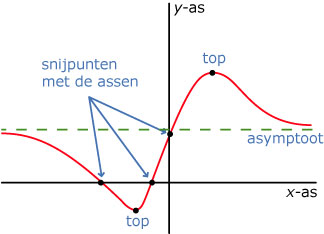
Als je de grafiek van een functie f goed in beeld hebt, zijn alle karakteristieken zichtbaar (op het gewenste domein). Dat zijn:

• de snijpunten met de assen, dat zijn de nulpunten en het snijpunt met de y-as;
• de asymptoten;
• de toppen, de punten met (locale) maxima en minima, die je met de grafische rekenmachine kunt opzoeken.

‡

Voorbeeld 1

De grafiek van `f(x)=(x+4)/(x-2)` heeft twee asymptoten.
Welke twee? Schrijf domein en bereik van f op.

Antwoord

Aangezien je niet door 0 kunt delen is er iets bijzonders als x – 2 = 0 en dus als x = 2.
f(2) bestaat niet, maar x-waarden vlak bij 2 kun je wel invullen: f(2,001) = 6001 en
f(2,0001) = 60001, etc. Verder is
f(1,999) = –5999 en f(1,9999) = –59999.
De grafiek van f komt dicht langs de lijn x = 2 te lopen: x = 2 is de vergelijking van de verticale asymptoot.

Voor de horizontale asymptoot ga je anders te werk:
Kies x-waarden als 1000, 10000, 100000, etc. Bereken de bijbehorende functiewaarden. Doe hetzelfde met –1000, –10000, –100000, etc. Je ziet dan dat de functiewaarden in de buurt van y = 1 komen te liggen. Hoe verder je van 0 af zit, hoe beter die benadering.
De lijn y = 1 is de horizontale asymptoot van de grafiek van f.

Het domein van f is: `(:larr,2:) uu (:2,larr:)`.
Het bereik van f is: `(:larr,-4:) uu (:-4,rarr:)`.

‡

Voorbeeld 2

Speelt de luchtweerstand geen rol, dan is de baan van een afgeschoten voorwerp P een zuivere parabool. Bijvoorbeeld h(x) = –0,005x² + x.
Hierin is x de horizontale afstand die het voorwerp heeft afgelegd (in meter) en h de bijbehorende hoogte boven de grond (in meter).
Bereken hoe hoog het voorwerp dan maximaal komt.

Antwoord

Bepaal eerst de nulwaarden door h(x) = 0 op te lossen. Je vindt: x = 0  V  x = 200.
Omdat een parabool symmetrisch is, zit het maximum bij x = 100.
En omdat f(100) = 50 komt het voorwerp maximaal 50 m hoog.

‡

Voorbeeld 3

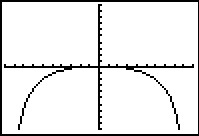Dit is een grafiek van de functie `f(x)=(4x^2-16)/(x^2-100)`.
Hij is gemaakt met een grafische rekenmachine met standaardvenster.

Bepaal alle karakteristieken en het bereik van f.

Antwoord

Op grond van dit plaatje zou je heel verkeerde conclusies kunnen trekken. Bijvoorbeeld dat het maximum f(0) = 0 is. En dat de grafiek een soort van afgeplatte bergparabool is. En dat is beslist niet goed...

Eerst maar even kijken of er nulpunten en asymptoten zijn:

• f(x) = 0 levert op: `(4x^2-16)/(x^2-100)=0` en dus: 4x² – 16 = 0.
  Er zijn daarom precies twee nulpunten (–2,0) en (2,0).

• Je deelt door x² – 100 en dus ontstaan er problemen als x² – 100 = 0.
  Dit betekent dat x = 10 en x = –10 wellicht verticale asymptoten zijn. Door getallen in de buurt van 10 dan wel –10 in te vullen, merk je dat dit echt twee vericale asymptoten zijn.

• Grote getallen (of grote, negatieve getallen) invullen en de functiewaarden naderen naar 4. Dus y = 4 is de horizontale asymptoot.

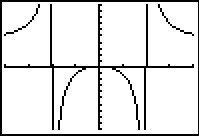
Pas nu de vensterinstellingen aan en breng alle karakteristieken van de grafiek in beeld.
Bij x = 0 blijkt een maximum te zitten: f(0) = 0,16.
(Laat je rekenmachine een maximum zoeken tussen bijvoorbeeld de nulwaarden.)

Het bereik van f lees je uit de grafiek af, rekening houdend met het maximum en de horizontale asymptoot:
B_f = `(:larr;0,16:) uu (:4,rarr:)`.

‡

Opgaven

2. Gegeven is de functie `f` met `f(x) = 4/x + 2`.
   1. Maak de grafiek van `f` met je grafische rekenmachine. Gebruik de standaardinstellingen van het venster.
   2. Welke verticale asymptoot heeft deze grafiek? Hoe zie je dat aan de tabel van `f`?
   3. Welk getal naderen de functiewaarden als `x` heel groot wordt?
   4. Welk getal naderen de functiewaarden als `x` heel klein wordt?
   5. Wat is de vergelijking van de horizontale asymptoot?
   6. Schrijf domein en bereik van `f` op.


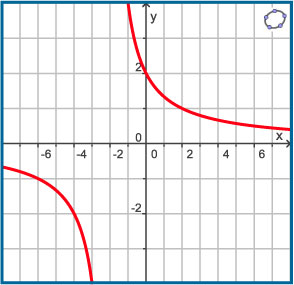3. Dit is een grafiek van de functie `f` met `f(x) = 4/(x+2)`.
   1. Welke verticale asymptoot heeft deze grafiek?
   2. Welk getal naderen de functiewaarden als `x` heel groot wordt?
   3. Welk getal naderen de functiewaarden als `x` heel klein wordt?
   4. Wat is de vergelijking van de horizontale asymptoot?
   5. Schrijf domein en bereik van `f` op.


4. In Voorbeeld 2 gaat het over een parabolische baan met `h(x) = -0,005x^2 + x`. In de applet zie je de grafiek ontstaan.
   1. Als je de grafiek met de GR wilt maken zijn de standaardinstellingen van het venster niet geschikt. Waarom niet?
   2. Om het hoogste punt te kunnen bepalen moet je de grafiek goed in beeld hebben. Waarom bereken je nu eerst de nulpunten?
   3. Maak vervolgens met je GR een geschikte tabel om te bekijken welke functiewaarden er allemaal voorkomen.
   4. Bij welke vensterinstellingen komt de hele baan in beeld?


5. Gegeven is de functie `f` met `f(x) = 100x(x - 10)(x - 20)^2`.
   1. Welke nulpunten heeft de grafiek van `f`?
   2. Waarom heeft de grafiek van `f` geen verticale asymptoot?
   Je kunt de `x`-waarden van het venster instellen, de nulpunten moeten zichtbaar worden en asymptoten zijn er niet. Met de tabel bekijk je de grootte van de functiewaarden.
   3. Welke vensterinstellingen laten alle karakteristieken zien?
   4. Bepaal de extremen van deze functie in gehele getallen nauwkeurig.
   5. Welk bereik heeft deze functie?


6. Bestudeer Voorbeeld 3.
   Gegeven is de functie `g` met `g(x) = (4x)/(1+x^2)`.
   1. Waarom heeft deze functie geen verticale asymptoot?
   2. Welk nulpunt heeft de grafiek van `g`?
   3. Onderzoek of `g` een horizontale asymptoot heeft.
   4. Schrijf domein en bereik van `g` op.

Verwerken

7. Schrijf bij de volgende functies de asymptoten en het domein en het bereik op.
   1. `f(x) = 4-4/x`
   2. `g(x)=(4-x)/x`
   3. `h(x)=x/(x^2-4)`
   4. `k(x)=x^2/(x^2+4)`


8. De hoogte van geluid wordt bepaald door de frequentie. Hoe hoger de frequentie hoe kleiner de golflengte wordt. De frequentie wordt uitgedrukt in Hertz (Hz) en geeft het aantal trillingen per seconde aan. Weet je de frequentie `f` dan kun je de golflengte `W` berekenen:
   `W = 330/f`
   Een geluidsinstallatie kan geluiden van 15 Hz tot 30000 Hz produceren.
   1. Als je `[15;30000]` als domein kiest, welk bereik heeft `W` dan?
   2. Vleermuizen kunnen hoogfrequentie geluiden horen, soms wel geluiden met een frequentie van 120000 Hz. Is dit een hoog of juist laag geluid? Welke golflengte heeft het?
   3. Mensen kunnen geluiden onder de 20 Hz nauwelijks horen. Gaat het dan om bassen of hoge tonen? Welke golflengte heeft zo’n geluid?
   4. Welke waarde benadert `W` als `f` heel groot wordt?


9. Gegeven is de functie `f` met `f(x) = (10x)/((x-20)^2)`.
   1. Bereken de nulpunten van deze functie.
   2. Welke asymptoten heeft deze functie?
   3. Bij welke vensterinstellingen is de grafiek van `f` goed in beeld met alle karakteristieken zichtbaar?
   4. Bepaal het bereik van `f`. (Benaderingen in twee decimalen nauwkeurig.)


10. Voor de totale kosten (`TK`) bij de productie van een bepaald artikel geldt:
    `TK = 100 + 0,1q^2` waarin `q` het aantal exemplaren voorstelt.
    1. Bereken de gemiddelde kosten per exemplaar bij een productie van 120 stuks in twee decimalen nauwkeurig.
    2. Leg uit, waarom de gemiddelde kosten het hellingsgetal zijn van de lijn door `(0,0)` en `(q,TK)`.
    3. Stel een voorschrift op voor de gemiddelde kosten per exemplaar (`GTK`) als functie van `q`.
    4. Welke asymptoot heeft de functie `GTK`? Schrijf domein en bereik van `GTK` op.

Testen

11. Gegeven is de functie `f` met `f(x) = (4+2x)/(x-1)`.
    1. Bereken `f(100)` en `f(-100)` in vier decimalen nauwkeurig.
    2. Bereken de nulpunten van de grafiek van `f`.
    3. Breng de grafiek van `f` in beeld.
    4. Schrijf de vergelijkingen van de asymptoten van de grafiek van `f` op.
    5. Schrijf domein en bereik van `f` op.


12. Gegeven is de functie `f` met `f(x) = x^2/(x^4+10)`.
    1. Bereken de nulpunten van de grafiek van deze functie.
    2. Welke asymptoten heeft deze functie?
    3. Bij welke vensterinstellingen is de grafiek van `f` goed in beeld met alle karakteristieken zichtbaar?
    4. Bepaal het bereik van `f`. (Benaderingen in twee decimalen nauwkeurig.)


13. In een biologisch laboratorium is onderzoek gedaan naar de tijd die zaden nodig hebben om voor 50% te ontkiemen. Proefondervindelijk is een verband tussen temperatuur en kiemtijd gebleken. De kiemtijd `K` is geteld in dagen en de temperatuur `T` is gemeten in °C. Dit verband wordt gegeven door: `K=89/(T-2)`.
    1. Boven welke temperatuur is de helft van de zaden al binnen 10 dagen ontkiemd?
    2. Wat is een zinvol domein voor `K` als functie van `T`?
    3. Welke asymptoten heeft de grafiek van deze functie?
    4. Welk bereik hoort bij het gekozen domein?