Karakteristieken

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Karakteristieken > Inleiding

Probeer de drie vragen in Verkennen te beantwoorden

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Karakteristieken > Uitleg

Opgaven

1. Bekijk de Uitleg en vooral het begrip asymptoot.
   Van een bepaald type kopieerapparaat worden de maandelijkse kosten per kopie gegeven door `K(a) = 200/a + 0,075`. Hierin is `a` het aantal kopieën per maand en `K` zijn de kosten in euro.
   1. Bereken de kosten per kopie als er 10000 kopieën per maand met deze machine worden gemaakt.
   2. Welke waarde benaderen de kosten per kopie als het aantal kopieën heel erg groot is?
   3. Welke horizontale asymptoot heeft de grafiek van `K`?
   4. Als er een bepaalde maand geen kopieën worden gemaakt, kun je niet spreken van de kosten per kopie. Het minimale aantal kopieën waarbij dit nog wel kan is 1. Hoeveel bedragen de kosten per kopie maximaal?

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Karakteristieken > Theorie

In de Theorie en in Voorbeeld 1 kun je zien hoe je de asymptoten van een functie berekent. Beweeg in Voorbeeld 1 punt `P` over de `x`-as.

Opgaven

2. Gegeven is de functie `f` met `f(x) = 4/x + 2`.
   1. Maak de grafiek van `f` met je grafische rekenmachine. Gebruik de standaardinstellingen van het venster.
   2. Welke verticale asymptoot heeft deze grafiek? Hoe zie je dat aan de tabel van `f`?
   3. Welk getal naderen de functiewaarden als `x` heel groot wordt?
   4. Welk getal naderen de functiewaarden als `x` heel klein wordt?
   5. Wat is de vergelijking van de horizontale asymptoot?
   6. Schrijf domein en bereik van `f` op.


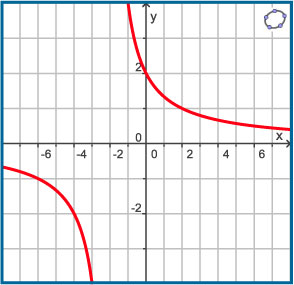3. Dit is een grafiek van de functie `f` met `f(x) = 4/(x+2)`.
   1. Welke verticale asymptoot heeft deze grafiek?
   2. Welk getal naderen de functiewaarden als `x` heel groot wordt?
   3. Welk getal naderen de functiewaarden als `x` heel klein wordt?
   4. Wat is de vergelijking van de horizontale asymptoot?
   5. Schrijf domein en bereik van `f` op.


4. In Voorbeeld 2 gaat het over een parabolische baan met `h(x) = -0,005x^2 + x`. In de applet zie je de grafiek ontstaan.
   1. Als je de grafiek met de GR wilt maken zijn de standaardinstellingen van het venster niet geschikt. Waarom niet?
   2. Om het hoogste punt te kunnen bepalen moet je de grafiek goed in beeld hebben. Waarom bereken je nu eerst de nulpunten?
   3. Maak vervolgens met je GR een geschikte tabel om te bekijken welke functiewaarden er allemaal voorkomen.
   4. Bij welke vensterinstellingen komt de hele baan in beeld?


5. Gegeven is de functie `f` met `f(x) = 100x(x - 10)(x - 20)^2`.
   1. Welke nulpunten heeft de grafiek van `f`?
   2. Waarom heeft de grafiek van `f` geen verticale asymptoot?
   Je kunt de `x`-waarden van het venster instellen, de nulpunten moeten zichtbaar worden en asymptoten zijn er niet. Met de tabel bekijk je de grootte van de functiewaarden.
   3. Welke vensterinstellingen laten alle karakteristieken zien?
   4. Bepaal de extremen van deze functie in gehele getallen nauwkeurig.
   5. Welk bereik heeft deze functie?


6. Bestudeer Voorbeeld 3.
   Gegeven is de functie `g` met `g(x) = (4x)/(1+x^2)`.
   1. Waarom heeft deze functie geen verticale asymptoot?
   2. Welk nulpunt heeft de grafiek van `g`?
   3. Onderzoek of `g` een horizontale asymptoot heeft.
   4. Schrijf domein en bereik van `g` op.

Verwerken

7. Schrijf bij de volgende functies de asymptoten en het domein en het bereik op.
   1. `f(x) = 4-4/x`
   2. `g(x)=(4-x)/x`
   3. `h(x)=x/(x^2-4)`
   4. `k(x)=x^2/(x^2+4)`


8. De hoogte van geluid wordt bepaald door de frequentie. Hoe hoger de frequentie hoe kleiner de golflengte wordt. De frequentie wordt uitgedrukt in Hertz (Hz) en geeft het aantal trillingen per seconde aan. Weet je de frequentie `f` dan kun je de golflengte `W` berekenen:
   `W = 330/f`
   Een geluidsinstallatie kan geluiden van 15 Hz tot 30000 Hz produceren.
   1. Als je `[15;30000]` als domein kiest, welk bereik heeft `W` dan?
   2. Vleermuizen kunnen hoogfrequentie geluiden horen, soms wel geluiden met een frequentie van 120000 Hz. Is dit een hoog of juist laag geluid? Welke golflengte heeft het?
   3. Mensen kunnen geluiden onder de 20 Hz nauwelijks horen. Gaat het dan om bassen of hoge tonen? Welke golflengte heeft zo’n geluid?
   4. Welke waarde benadert `W` als `f` heel groot wordt?


9. Gegeven is de functie `f` met `f(x) = (10x)/((x-20)^2)`.
   1. Bereken de nulpunten van deze functie.
   2. Welke asymptoten heeft deze functie?
   3. Bij welke vensterinstellingen is de grafiek van `f` goed in beeld met alle karakteristieken zichtbaar?
   4. Bepaal het bereik van `f`. (Benaderingen in twee decimalen nauwkeurig.)


10. Voor de totale kosten (`TK`) bij de productie van een bepaald artikel geldt:
    `TK = 100 + 0,1q^2` waarin `q` het aantal exemplaren voorstelt.
    1. Bereken de gemiddelde kosten per exemplaar bij een productie van 120 stuks in twee decimalen nauwkeurig.
    2. Leg uit, waarom de gemiddelde kosten het hellingsgetal zijn van de lijn door `(0,0)` en `(q,TK)`.
    3. Stel een voorschrift op voor de gemiddelde kosten per exemplaar (`GTK`) als functie van `q`.
    4. Welke asymptoot heeft de functie `GTK`? Schrijf domein en bereik van `GTK` op.

Testen

11. Gegeven is de functie `f` met `f(x) = (4+2x)/(x-1)`.
    1. Bereken `f(100)` en `f(-100)` in vier decimalen nauwkeurig.
    2. Bereken de nulpunten van de grafiek van `f`.
    3. Breng de grafiek van `f` in beeld.
    4. Schrijf de vergelijkingen van de asymptoten van de grafiek van `f` op.
    5. Schrijf domein en bereik van `f` op.


12. Gegeven is de functie `f` met `f(x) = (x^2)/(x^4+10)`.
    1. Bereken de nulpunten van de grafiek van deze functie.
    2. Welke asymptoten heeft deze functie?
    3. Bij welke vensterinstellingen is de grafiek van `f` goed in beeld met alle karakteristieken zichtbaar?
    4. Bepaal het bereik van `f`. (Benaderingen in twee decimalen nauwkeurig.)


13. In een biologisch laboratorium is onderzoek gedaan naar de tijd die zaden nodig hebben om voor 50% te ontkiemen. Proefondervindelijk is een verband tussen temperatuur en kiemtijd gebleken. De kiemtijd `K` is geteld in dagen en de temperatuur `T` is gemeten in °C. Dit verband wordt gegeven door: `K=(89)/(T-2)`.
    1. Boven welke temperatuur is de helft van de zaden al binnen 10 dagen ontkiemd?
    2. Wat is een zinvol domein voor `K` als functie van `T`?
    3. Welke asymptoten heeft de grafiek van deze functie?
    4. Welk bereik hoort bij het gekozen domein?