Domein en bereik

Inleiding

Bij veel functies kun je niet zomaar elk getal invoeren. Zeker niet als ze 'ergens over gaan'. Ook als uitkomst is vaak niet alles mogelijk, regelmatig vallen ze binnen bepaalde grenzen. Om die beperkingen aan te geven is een speciale notatie nodig.

Je leert nu:

• de intervalnotatie gebruiken om te kunnen aangeven dat waarden beperkt zijn;
• het begrip domein gebruiken voor de mogelijk invoerwaarden;
• het begrip bereik gebruiken voor de mogelijke uitkomsten.

Je kunt al:

• het begrip functie en de bijbehorende notaties gebruiken;
• grafieken van functies goed in beeld brengen.

Verkennen

Werk van het practicum "Functies met de GR" het deel door dat gaat over het bepalen van de toppen van een grafiek.

In de toppen van een grafiek heeft de bijbehorende functie een maximum (grootste functiewaarde) of een minimum (kleinste functiewaarde).

> Liggen alle functiewaarden altijd tussen het minimum en het maximum? Bedenk eens wat verschillende situaties.
> Zijn er situaties te bedenken dat je niet zomaar alle reële getallen in een functie kunt invoeren? Geef voorbeelden.
> Hoe zou je kunnen aangeven welke invoerwaarden en welke functiewaarden bij een functie kunnen voorkomen?

Uitleg

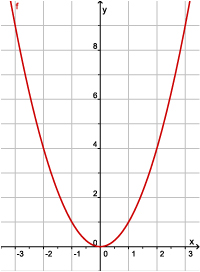
Hier zie je de grafiek van de functie f(x) = x².
Je weet dat deze grafiek een parabool is.

Van elk reëel getal x kun je het kwadraat uitrekenen, dus er zijn geen beperkingen voor de invoerwaarden. De kleinste functiewaarde is: f(0) = 0.
In de wiskunde worden de woorden "domein" en "bereik" gebruikt:

• het domein is de verzameling van alle mogelijke invoerwaarden; bij functie f is het domein daarom de verzameling van alle reële getallen;
• het bereik is de verzameling van alle mogelijke uitkomsten: bij functie f is het bereik daarom de verzameling van alle reële getallen groter dan of gelijk aan 0.

Korter gezegd:

• het domein is: D_f = `RR`.
• het bereik is: B_f = `[0,rarr:)`

De notatie `[0,rarr:)` voor alle reële getallen groter dan of gelijk aan 0 is een voorbeeld van de notatie als interval.

Een interval is eigenlijk niks anders dan een aaneengesloten verzameling reële getallen, een stukje van een getallenlijn. De notatie ervan is op zich eenvoudig: je schrijft de grenswaarden (de grootste en de kleinste waarden, de kleinste eerst) van het interval op tussen twee haakjes. Er zijn alleen twee afspraken die je erbij moet onthouden:

• de vorm van de haakjes bepaalt of de grenswaarde nog wel bij het interval hoort of juist niet meer;
• voor intervallen die aan één kant geen grenswaarde hebben gebruik je een pijltje.

Hier zie je voorbeelden van intervallen met het bijbehorend deel van de getallenlijn.

‡

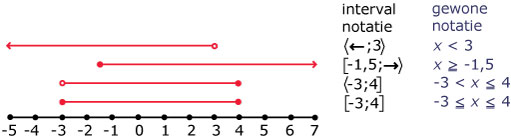
Opgaven

1. Bekijk de eerste pagina van de Uitleg. Voor een windmolen geldt `P(v) = 0,052v^3`. Daarin is `P` het vermogen in kW en `v` de windsnelheid in m/s. Bij windsnelheden boven de 30 m/s loopt de windmolen risico van beschadiging. Hij slaat dan automatisch af.
   1. De verschillende windsnelheden die mogelijk zijn in deze situatie vormen het domein van de functie `P(v)`. Je schrijft een domein als interval, zie pagina 2 van de Uitleg. Schrijf het domein van `P` op deze wijze op.
   2. Welke waarden voor `P` horen bij dit domein? Schrijf het bereik van `P` ook als interval.
   3. Als je niet kijkt naar de praktijksituatie, maar alleen naar het functievoorschrift, welk domein en welk bereik heeft de functie `P(v)` dan?


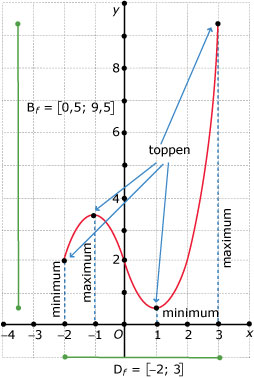
2. Gegeven is de functie `f` met voorschrift `f(x) = 4 - x^2`.
   1. Welke waarden kan `x` aannemen? Schrijf het domein van `f` op.
   2. Bereken algebraïsch de snijpunten van `f` met de assen.
   3. Bekijk de grafiek van deze functie. Schrijf het bereik op.
   4. Stel je neemt als domein van `f` het interval `[-1,3]`. Wat is dan het bijbehorende bereik?

Theorie

Alle toegestane invoerwaarden samen vormen het domein van een functie. Het domein wordt bepaald door

• beperkingen vanwege het functievoorschrift;
• beperkingen vanuit de situatie.

Het domein van functie f wordt aangegeven door D_f.

Alle mogelijke functiewaarden samen vormen het bereik van een functie. Om het bereik van een functie f te kunnen bepalen je een goed beeld van de grafiek van f nodig. Daarbij zijn de toppen van een grafiek vaak van belang. In een top heeft de functie een maximum (grootste functiewaarde) of een minimum (kleinste functiewaarde). Het bereik van functie f wordt aangegeven door B_f.

Voor domein en bereik van een functie wordt meestal de intervalnotatie gebruikt.
Een interval is een aaneengesloten verzameling reële getallen, een stukje getallenlijn dus. In de "Uitleg" zie je er een paar met het bijbehorende deel van de getallenlijn.
Alle reële getallen noteer je als `RR`.

‡

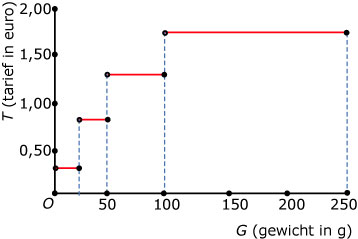
Voorbeeld 1

De TPG-tarieven voor de brievenbuspost binnenland zijn in 2007:

• van 0 tot en met 20 gram: € 0,44
• van 20 tot en met 50 gram: € 0,88
• van 50 tot en met 100 gram: € 1,32
• van 100 tot en met 250 gram: € 1,76

Het tarief T is een functie van het gewicht g.
Geef domein en bereik van die functie.

Antwoord

Het domein van T(g) wordt bepaald door de situatie:
alleen gewichten van 0 tot en met 250 gram hebben een tarief als brievenbuspost.
Dus: D_T = [0, 250].

Het bereik van T(g) wordt ook door de situatie bepaald:
alleen enkele losse getallen zijn als uitkomst mogelijk.
Je zet die getallen dan tussen accolades: B_T = {0,44; 0,88; 1,32; 1,76}.

‡

Voorbeeld 2

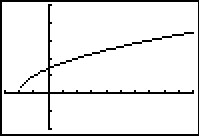
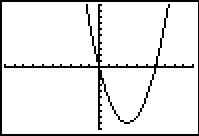
Met je grafische rekenmachine kun je (een deel van) de grafiek van `f(x)=sqrt(x+2)` goed in beeld brengen. Je ziet hem hiernaast. Geef domein en bereik van f.

Antwoord

Je weet dat de functiewaarden groter worden naarmate je een groter getal voor x kiest. Het kleinste getal dat mogelijk is als invoerwaarde is x = –2.
Je krijgt dan als functiewaarde: `f(-2)=sqrt(-2+2)=0`.

Hier bepaalt het functievoorschrift wat domein en bereik zijn:

• de wortel uit een negatief getal is niet reëel, dus: D_f = `[-2,rarr:)`
• de functiewaarden zijn 0 of groter, dus: B_f = `[0,rarr:)`

De gebruikte vensterinstellingen zijn [–3,10] × [–2,5].
(Hierbij geef je eerst de instellingen voor x en als tweede die voor y.)

‡

Voorbeeld 3

Je ziet hier (een deel van) de grafiek van f(x) = 0,5x⁴ – 4x²
Bepaal domein en bereik van deze functie.

Antwoord

Bij elke waarde van x kun je x⁴ en x² berekenen en dus ook een functiewaarde. Het domein van f is dus D_f = `RR`.

Voor het bereik moet je de grafiek even goed bekijken. Er zijn drie toppen, die je gemakkelijk kunt vinden.
In het practicum "Functies met de GR" kun je nalezen hoe dat met de GR gaat.
Je vindt een minimum f(–2) = –8 en een minimum f(2) = –8.
Verder is er een maximum f(0) = 0, maar dat is voor het bereik onbelangrijk.
Ga na: B_f = `[-8,rarr:)`.

‡

Opgaven

3. Bekijk Voorbeeld 2. Gegeven is nu de functie `f` met `f(x) = 1 - sqrt(x)`.
   1. Welke waarden kan `x` aannemen? Schrijf het domein van `f` op.
   2. Bereken algebraïsch de snijpunten van de grafiek van `f` met de assen.
   3. Bekijk de grafiek van `f`. Schrijf het bereik van `f` op.


4. Voorbeeld 3 gaat over de functie `f` met `f(x) = 0,5x^4 - 4x^2`.
   1. Hoeveel is `f(-1)`? En hoeveel is `f(3)`?
   2. Schrijf zelf de maxima en de minima van `f` op.
   3. Stel je voor dat je als domein van `f` het interval `[-1,2]` neemt. Wat is dan het bijbehorende bereik?
   4. Welke domeinen horen bij het bereik `[0,5]`? Noem er minstens twee.


5. Gegeven de functie `f(x) = 400 - (x - 10)^2`.
   Het domein van deze functie is `[0,40]`.
   1. Breng de grafiek met je grafische rekenmachine goed in beeld. Bekijk eventueel Voorbeeld 2 nog eens.
   2. Welke top heeft de grafiek van `f` als je niet op het domein let?
   3. Bepaal het bereik van `f`. (Let op het gegeven domein!)


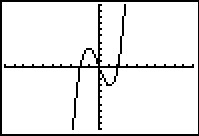
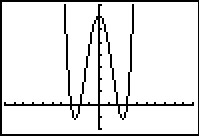
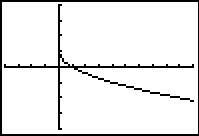
6. Hier zie je steeds de grafiek van een functie. Alle toppen en nulpunten zijn in beeld. Schrijf domein en bereik van deze functie op. Geef waar nodig benaderingen in twee decimalen nauwkeurig.
   
   

   `f(x) = x^2 - 4x`	`g(x) = x^3 - 4x`	`h(x) = (x^2 - 4)(x^2 - 9)`	`k(x) = -6 + 3 sqrt(x+7)`



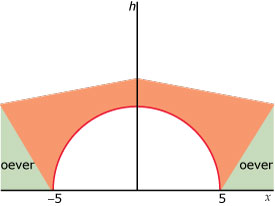
7. De boog onder een brug heeft de vorm van de grafiek van `h(x) = sqrt(25-x^2)` . Het lijnstuk tussen beide nulpunten van deze functie stelt de rivierbodem voor.
   1. Hoe lang is dat lijnstuk?
   2. Wat is het domein van deze functie?
   3. Wat is het bereik van deze functie?
   4. De waterhoogte van de rivier is 2 meter boven de bodem. Bereken de breedte van de waterspiegel onder deze boog in centimeter nauwkeurig.

Verwerken

9. Bepaal van de volgende functies het domein en het bereik. Noteer ze als interval. (Eventuele benaderingen in twee decimalen.)
   1. `f(x) = x^2 - x - 6`
   2. `g(x) = x^2(x - 2)(x - 3)`
   3. `h(x) = x^3 - 6x`
   4. `k(x)=1+2 sqrt(x)`


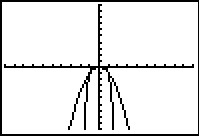
10. Hier zie je de grafieken van de functies `f` en `g` met `f(x) = x^2 - 2x^4` en `g(x) = -x^2` met de standaardinstellingen van het venster.
    1. Bereken algebraïsch de nulwaarden van `f`.
    2. De standaardinstellingen zijn niet erg gelukkig als je de toppen en de nulpunten van beide functies wilt zien. Kies betere instellingen en bepaal de toppen van de grafiek van `f`.
    3. Bepaal van beide functies het bereik.
    4. Bereken algebraïsch de snijpunten van de grafieken van `f` en `g`.


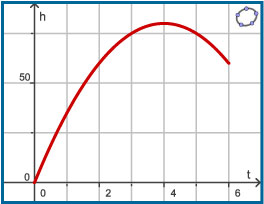
11. Een vuurpijl wordt vanaf de grond afgeschoten. De hoogte boven de grond hangt daarna tot hij uit elkaar spat af van de tijd. Er geldt: `h(t) = 40t - 5t^2`. Hierin is `h` de hoogte boven de grond in meter en `t` de tijd in seconden.
    1. De vuurpijl spat na 6 seconden uit elkaar. Hoe hoog komt hij maximaal?
    2. Schrijf domein en bereik van deze functie op, rekening houdend met de beschreven situatie.
    3. Op welke hoogte spat de vuurpijl uit elkaar?
    4. Hoeveel seconden is de vuurpijl zichtbaar boven een rij bomen van 40 m hoogte?
    5. Waarom is de getekende grafiek niet de baan van de vuurpijl?


12. Een handelaar heeft wekelijks 400 exemplaren van een bepaald product in de verkoop. Hij heeft geen concurrentie, dus de hoeveelheid `q` die hij verkoopt hangt alleen af van de prijs `p` die hij per exemplaar vraagt. Er geldt: `q = 400 - 0,5p`.
    1. Geef een formule voor de opbrengst `R` als functie van de prijs `p`.
    2. Welke waarden kan `p` aannemen?
    3. Welke waarden kan `R` aannemen?


13. Gegeven is de functie `f` met `f(x) = -2(x - 10)^2 + 60` en domein `[0,40]`. Bepaal het bereik van `f`.

Testen

15. Breng de grafiek van deze functies in beeld met de standaardinstellingen van het venster. Schrijf domein en bereik van deze functies op.
    1. `f(x) = 4 - (x - 2)^2`
    2. `g(x)=4`
    3. `h(x)=2+sqrt(4-x)`


16. Gegeven is het functievoorschrift `y(x) = x^4 - 8x^2`.
    1. Bereken `y(3)` en `y(-3)`.
    2. Bereken algebraïsch de nulpunten van de grafiek van `y(x)`.
    3. Bepaal met behulp van de grafische rekenmachine de toppen van de grafiek.
    4. Schrijf het bereik van deze functie op.


17. Hangbruggen zijn bruggen die zijn opgehangen aan zware spankabels. Die spankabels hangen op hun beurt aan stalen masten of stenen torens. Hier zie je een spankabel hangen tussen twee torens van 90 meter hoog. Er geldt: `h(x) = frac{9}{50} x^2 + 5`.
    1. Laat zien dat de tuidraad bij `x = 10` een lengte heeft van 23 meter.
    2. Welk domein heeft de functie `h` in de beschreven situatie?
    3. Welk bereik heeft de functie `h` dan?
    4. Er zijn twee tuidraden met een lengte van 45,5 meter. Hoe ver hangen deze twee tuidraden van elkaar?