
Domein en bereik
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Domein en bereik > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Domein en bereik > Inleiding
Werk het Practicum "Functies en de [GR]" door tot aan "Families van functies".
Onthoud alvast de uitdrukking karakteristieken van een functie.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Domein en bereik > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Domein en bereik > Uitleg
Opgaven
-
Bekijk de eerste pagina van de Uitleg.
Voor een windmolen geldt `P(v) = 0,052v^3`.
Daarin is `P` het vermogen in kW en `v` de windsnelheid in m/s.
Bij windsnelheden boven de 30 m/s loopt de windmolen risico van beschadiging.
Hij slaat dan automatisch af.
-
De verschillende windsnelheden die mogelijk zijn in deze situatie vormen het domein van de functie `P(v)`.
Je schrijft een domein als interval, zie pagina 2 van de Uitleg.
Schrijf het domein van `P` op deze wijze op.
- Welke waarden voor `P` horen bij dit domein? Schrijf het bereik van `P` ook als interval.
-
Als je niet kijkt naar de praktijksituatie, maar alleen naar het functievoorschrift,
welk domein en welk bereik heeft de functie `P(v)` dan?
-
Gegeven is de functie `f` met voorschrift `f(x) = 4 - x^2`.
-
Welke waarden kan `x` aannemen? Schrijf het domein van `f` op.
-
Bereken algebraïsch de snijpunten van `f` met de assen.
-
Bekijk de grafiek van deze functie. Schrijf het bereik op.
-
Stel je neemt als domein van `f` het interval `[-1,3]`.
Wat is dan het bijbehorende bereik?
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Domein en bereik > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Domein en bereik > Theorie
Bestudeer de Theorie.
Let goed op de termen "maximum", "minimum", "domein" en "bereik".
Opgaven
-
Bekijk Voorbeeld 2.
Gegeven is nu de functie `f` met `f(x) = 1 - sqrt(x)`.
-
Welke waarden kan `x` aannemen? Schrijf het domein van `f` op.
-
Bereken algebraïsch de snijpunten van de grafiek van `f` met de assen.
-
Bekijk de grafiek van `f`. Schrijf het bereik van `f` op.
-
In Voorbeeld 3 kun je de functiewaarden van functie `f` met `f(x) = 0,5x^4 - 4x^2` aflezen door de zwarte punt over de `x`-as te bewegen.
-
Hoeveel is `f(-1)`? En hoeveel is `f(3)`?
-
Schrijf zelf de maxima en de minima van `f` op.
-
Stel je voor dat je als domein van `f` het interval `[-1,2]` neemt. Wat is dan het bijbehorende bereik?
-
Welke domeinen horen bij het bereik `[0,5]`? Noem er minstens twee.
-
Gegeven de functie `f(x) = 400 - (x - 10)^2`.
Het domein van deze functie is `[0,40]`.
-
Breng de grafiek met je grafische rekenmachine goed in beeld. Bekijk eventueel Voorbeeld 2 nog eens.
-
Welke top heeft de grafiek van `f` als je niet op het domein let?
-
Bepaal het bereik van `f`. (Let op het gegeven domein!)
-
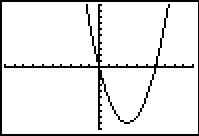
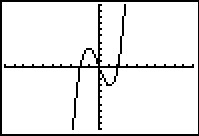
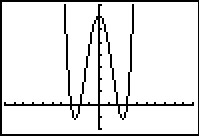
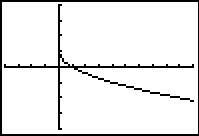
Hier zie je steeds de grafiek van een functie. Alle toppen en nulpunten zijn in beeld. Schrijf domein en bereik van deze functie op. Geef waar nodig benaderingen in twee decimalen nauwkeurig.
| `f(x) = x^2 - 4x` | `g(x) = x^3 - 4x` | `h(x) = (x^2 - 4)(x^2 - 9)` | `k(x) = -6 + 3 sqrt(x+7)` |
 |
 |
 |
 |
-
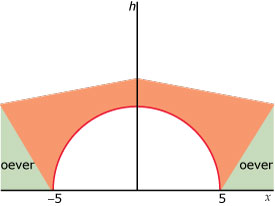 De boog onder een brug heeft de vorm van de grafiek van `h(x) = sqrt(25-x^2)`.
Het lijnstuk tussen beide nulpunten van deze functie stelt de rivierbodem voor.
De boog onder een brug heeft de vorm van de grafiek van `h(x) = sqrt(25-x^2)`.
Het lijnstuk tussen beide nulpunten van deze functie stelt de rivierbodem voor.
-
Hoe lang is dat lijnstuk?
-
Wat is het domein van deze functie?
-
Wat is het bereik van deze functie?
-
De waterhoogte van de rivier is 2 meter boven de bodem.
Bereken de breedte van de waterspiegel onder deze boog in centimeter nauwkeurig.
Verwerken
-
Bepaal van de volgende functies het domein en het bereik. Noteer ze als interval. (Eventuele benaderingen in twee decimalen.)
-
`f(x) = x^2 - x - 6`
-
`g(x) = x^2(x - 2)(x - 3)`
-
`h(x) = x^3 - 6x`
-
`k(x)=1+2 sqrt(x)`
-
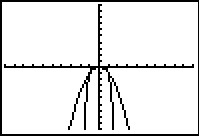
Hier zie je de grafieken van de functies `f` en `g` met `f(x) = x^2 - 2x^4` en `g(x) = -x^2` met de standaardinstellingen van het venster.
-
Bereken algebraïsch de nulwaarden van `f`.
-
De standaardinstellingen zijn niet erg gelukkig als je de toppen en de nulpunten van beide functies wilt zien.
Kies betere instellingen en bepaal de toppen van de grafiek van `f`.
-
Bepaal van beide functies het bereik.
-
Bereken algebraïsch de snijpunten van de grafieken van `f` en `g`.
-
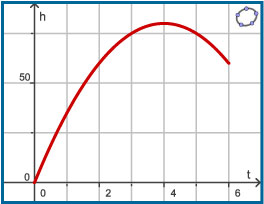
Een vuurpijl wordt vanaf de grond afgeschoten. De hoogte boven de grond hangt daarna tot hij uit elkaar spat af van de tijd. Er geldt: `h(t) = 40t - 5t^2`. Hierin is `h` de hoogte boven de grond in meter en `t` de tijd in seconden.
-
De vuurpijl spat na 6 seconden uit elkaar. Hoe hoog komt hij maximaal?
-
Schrijf domein en bereik van deze functie op, rekening houdend met de beschreven situatie.
-
Op welke hoogte spat de vuurpijl uit elkaar?
-
Hoeveel seconden is de vuurpijl zichtbaar boven een rij bomen van 40 m hoogte?
-
Waarom is de getekende grafiek niet de baan van de vuurpijl?
-
Een handelaar heeft wekelijks 400 exemplaren van een bepaald product in de verkoop. Hij heeft geen concurrentie, dus de hoeveelheid `q` die hij verkoopt hangt alleen af van de prijs `p` die hij per exemplaar vraagt.
Er geldt: `q = 400 - 0,5p`.
-
Geef een formule voor de opbrengst `R` als functie van de prijs `p`.
-
Welke waarden kan `p` aannemen?
-
Welke waarden kan `R` aannemen?
-
Gegeven is de functie `f` met `f(x) = -2(x - 10)^2 + 60` en domein `[0,40]`.
Bepaal het bereik van `f`.
Testen
-
Breng de grafiek van deze functies in beeld met de standaardinstellingen van het venster.
Schrijf domein en bereik van deze functies op.
-
`f(x) = 4 - (x - 2)^2`
-
`g(x)=4`
-
`h(x)=2+sqrt(4-x)`
-
Gegeven is het functievoorschrift `y(x) = x^4 - 8x^2`.
-
Bereken `y(3)` en `y(-3)`.
-
Bereken algebraïsch de nulpunten van de grafiek van `y(x)`.
-
Bepaal met behulp van de grafische rekenmachine de toppen van de grafiek.
-
Schrijf het bereik van deze functie op.

-
Hangbruggen zijn bruggen die zijn opgehangen aan zware spankabels.
Die spankabels hangen op hun beurt aan stalen masten of stenen torens.
Hier zie je een spankabel hangen tussen twee torens van 90 meter hoog.
Er geldt: `h(x) = frac{9}{50} x^2 + 5`.
-
Laat zien dat de tuidraad bij `x = 10` een lengte heeft van 23 meter.
-
Welk domein heeft de functie `h` in de beschreven situatie?
-
Welk bereik heeft de functie `h` dan?
-
Er zijn twee tuidraden met een lengte van 45,5 meter. Hoe ver hangen deze twee tuidraden van elkaar?

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Domein en bereik > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Domein en bereik > Inleiding
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Domein en bereik > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Domein en bereik > Uitleg
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Domein en bereik > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Domein en bereik > Theorie
 De boog onder een brug heeft de vorm van de grafiek van `h(x) = sqrt(25-x^2)`.
Het lijnstuk tussen beide nulpunten van deze functie stelt de rivierbodem voor.
De boog onder een brug heeft de vorm van de grafiek van `h(x) = sqrt(25-x^2)`.
Het lijnstuk tussen beide nulpunten van deze functie stelt de rivierbodem voor.


