
Het begrip functie
Inleiding
Je hebt al met formules gewerkt.
Soms beschrijft een formule een verband tussen twee variabelen.
Voer je voor de éne een getal in, kun je vaak de andere variabele uitrekenen.
Komt er dan telkens precies één uitkomst (en niet meerdere), dan spreek je van een functie.
In dit deel zal worden ingegaan op wat een functie nou precies is.
En hoe je er een grafiek bij kunt (laten) maken.
Je leert nu:
- wat er onder een functie wordt verstaan;
- hoe je de grafiek van een functie maakt;
- grafieken van functies met je grafische rekenmachine maken.
Je kunt al:
- met formules werken: erin invullen en ze herschrijven;
- eenvoudige vergelijkingen oplossen.
Verkennen
Bekijk je grafische rekenmachine maar eens goed.
Zorg ervoor dat hij werkt met de basisinstellingen.
En zorg er voor dat de machine zo is ingesteld dat er formules van de vorm y = ... kunnen worden ingevoerd.
Deze instelling heeft gevolgen voor de knoppen direct onder het venster.
Daarmee maak je grafieken en dergelijke.
> Hoe krijg je een grafiek bij y = (x – 10)2 + 100 te zien?
> Hoe krijg je een grafiek bij x + y = 10 te zien?

Uitleg
Je ziet op veel plaatsen windmolens om elektriciteit op te wekken.
Het vermogen dat zo'n molen levert hangt af van de dubbele wieklengte D en van de windsnelheid v.
Het vermogen van een zeker type windmolen wordt gegeven door de formule:
P = 0,00013 · v3 · D2
Hierin is P het (gemiddelde) vermogen in kW (kiloWatt), v de (gemiddelde) windsnelheid in m/s (meter per seconde) en D de diameter van de cirkel die de uiterste punt van een wiek maakt bij het draaien in m (meter).
Bij een diameter van 20 m en een windsnelheid van 10 m/s is het vermogen P = 0,00013 · 103 · 402 ≈ 52 kW.
Je bekijkt een windmolen met wieken van 10 m.
Je wilt snel een tabel maken van het vermogen bij verschillende windsnelheden.
Vul dan D = 20 in en schrijf de formule als P = 0,052 · v3.
Om extra duidelijk te maken dat P afhangt van v schrijf je liever: P(v) = 0,052 · v3.
Zoiets heet een functievoorschrift en P is een functie van v.
Bij elke waarde van v hoort precies één uitkomst: bij v = 10 hoort P = 52.
Dit schrijf je korter als P(10) = 52.
En in plaats van uitkomst noem je 52 een functiewaarde.
Met je grafische rekenmachine kun je bij de functie met voorschrift
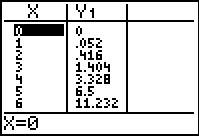
P(v) = 0,052 · v3 een tabel en een grafiek maken.
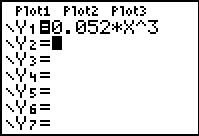
Je voert de formule dan in je grafische rekenmachine in als
Y1=0.052*X^3.
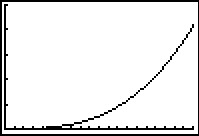
Daarna stel je de afmetingen van het venster in en maak je de grafiek.
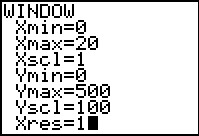
Bestaan er ook verbanden die geen functie zijn?
Jazeker, neem het verband x2 + y2 = 100.
Kies je als invoerwaarde x = 0, dan vind je twee mogelijke waarden voor y, namelijk 10 en –10.
En daarom is y geen functie van x.
‡
Opgaven
-
Bekijk de Uitleg.
Voor de windmolen met wieken van 10 m geldt `P(v) = 0,052v^3`.
Daarin is `P` het vermogen in kW en `v` de windsnelheid in m/s.
-
Bereken `P(6)` betekent:
A - Bereken de functiewaarde bij invoerwaarde `v = 6`.
B - Bereken de invoerwaarde bij functiewaarde `v = 6`.
C - Bereken de functiewaarde als `P = 6`.
D - Bereken de invoerwaarde als `P = 6`.
- Bereken `P(6)`.
-
Windsnelheden van 0 tot 15 m/s komen in de kustgebieden regelmatig voor.
Breng het deel van de grafiek van `P` dat daarbij hoort in beeld op je grafische rekenmachine.
Welke waarden voor `P` horen daar bij?
-
Voor welke waarde van `v` geldt: `P(v) = 300`? Licht het antwoord toe.
-
Neem nu een windmolen met wieklengte 20 m.
-
Welk voorschrift geldt nu voor `P` als functie van `v`?
-
Bereken `P(10)`.
-
Breng de grafiek in beeld voor windsnelheden vanaf 0 tot en met 20 m/s.
Welke vensterinstellingen heb je nodig om de complete grafiek in beeld te krijgen?
-
Bij welke windsnelheid in km/h is het vermogen 40 kW?
-
Bekijk het laatste deel de Uitleg.
-
Geef nog een voorbeeld waaruit blijkt dat de formule `x^2 + y^2 = 100` geen functievoorschrift is.
-
Schrijf deze formule in de vorm `y =` ...
-
Door welke twee functievoorschriften `y_1` en `y_2` kun je de formule vervangen?
-
Breng nu de grafieken van deze twee functies in beeld. Welke vensterinstellingen gebruik je?
-
Bereken `y_1(5)` en `y_2(5)`.
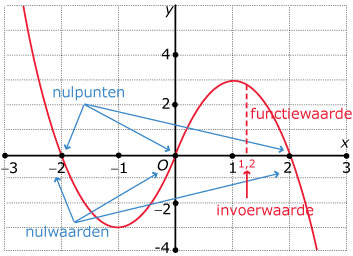
Theorie
Bij een formule zoals y = –x3 + 4x vind je bij elke waarde van x precies één waarde van y. In dat geval is y een functie van x met functievoorschrift y(x) = –x3 + 4x.
Bij een functie kun je een tabel maken en een grafiek tekenen.
De invoerwaarden komen op de horizontale as, de x-as.
De uitkomsten heten functiewaarden.
y(1) = –13 + 4 · 1 = 3 is de functiewaarde bij x = 1. Functiewaarden komen op de y-as.
Voor y(x) wordt ook wel f(x) gebruikt. y is dan een functie van x die f heet.
In praktijksituaties gebruik je vaak letters die verwijzen naar de betekenis van de variabelen.
Bijvoorbeeld t voor tijd, l voor lengte, I voor inhoud, v voor snelheid,
P voor vermogen, enzovoort.
Je grafische rekenmachine werkt standaard met X voor invoerwaarden en Y voor functiewaarden.
De nulwaarden van een functie zijn de invoerwaarden waarbij de functiewaarde (de uitkomst dus) 0 is.
Bij de gegeven functie zijn het de x-waarden waarvoor geldt:
y(x) = –x3 + 4x = 0.
Hier zijn het de waarden x = 0, x = –2 en x = 2.
De bijbehorende nulpunten zijn (0, 0), (–2, 0) en (2, 0).
‡
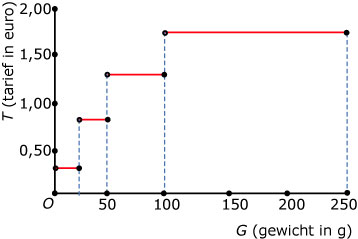
Voorbeeld 1
De TPG-tarieven voor de brievenbuspost binnenland zijn in 2006:
- van 0 tot en met 20 gram: € 0,44
- van 20 tot en met 50 gram: € 0,88
- van 50 tot en met 100 gram: € 1,32
- van 100 tot en met 250 gram: € 1,76
Is het tarief een functie van het gewicht?
Is het gewicht een functie van het tarief?
Antwoord
Bij elke (toegestane) waarde voor het gewicht G vind je precies één
tarief T. Dus T is een functie van G.
Een functievoorschrift is niet eenvoudig te geven.
Een grafiek tekenen lukt wel...
Omgekeerd is G geen functie van T. Als je het bedrag weet, kun je namelijk nog niet
precies zeggen hoe zwaar het poststuk is, daar zijn meerdere mogelijkheden voor.
‡
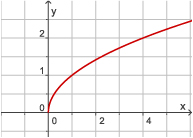
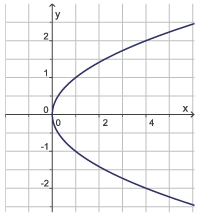
Voorbeeld 2
Hier zie je twee formules bij verbanden tussen x en y:
- y = `sqrt(x)`
- y2 = x
Verder zie je grafieken bij deze verbanden, de bovenste hoort bij 1.
 Is y een functie van x bij formule 1?
Is y een functie van x bij formule 1?
Is y een functie van x bij formule 2?
Antwoord
Kies bijvoorbeeld: x = 4.
Bij verband 1 vind je dan: y = 2.
Bij verband 2 vind je dan: y = 2 V y = –2.
Bij verband 1 vind je zo bij elke waarde voor x precies één waarde
van y, of geen enkele waarde van y (als x negatief is).
Dus bij verband 1 is y een functie van x
Bij verband 2 vind je bij vrijwel alle x-waarden twee waarden van y.
Alleen bij x = 0 vind je er maar één.
En bij negatieve x-waarden vind je weer geen uitkomsten.
Dus bij verband 2 is y geen functie van x.
‡
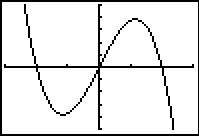
Voorbeeld 3
Hier zie je de grafiek van de functie f met functievoorschrift
f(x) = 10x – 0,1x3.
De grafiek is gemaakt met de grafische rekenmachine.
Welke instellingen moet je het venster geven om hem zo in beeld te krijgen?
En hoe weet je zeker dat je dan alle belangrijke punten van de grafiek in beeld hebt?
Antwoord
Je wilt bij een grafiek (als dat enigszins kan) alle snijpunten met de assen en de toppen
in beeld hebben. Om zeker te weten dat je alle snijpunten met de assen hebt, bereken
je eerst de nulwaarden:
10x – 0,1x3 = 0
100x – x3 = 0
x(100 – x2) = 0
De nulwaarden zijn daarom x = 0 en x = ±10.
De nulpunten zijn (–10, 0), (0, 0) en (10, 0).
Vervolgens bekijk je de tabel die je rekenmachine maakt vanaf x = –15 t/m x = 15.
Je ziet dan dat de functiewaarden liggen tussen –50 en 50.
Dus moet je voor de kleinste y-waarde –50 en voor de grootste y-waarde 50 instellen.
(Het aantal schaalstreepjes op de as kun je ook nog instellen!)
‡
Opgaven
-
Gegeven is de functie `f` met voorschrift `f(x)=x^2-4x`.
Welke van deze uitspraken zijn waar?
A - `f(4)` is een invoerwaarde
B - `f(10) = 60` betekent dat het punt (60;10) op de grafiek ligt.
C - `f(x) = 5` heeft twee oplossingen.
D - Bij elke waarde van x hoort precies één waarde van y.
-
Bekijk nog eens de functie `f` met voorschrift `f(x)=x^2-4x`.
-
Bereken de nulwaarden van `f`.
-
Welke nulpunten heeft de grafiek van `f`?
-
Los op: `f(x)=5`.
-
In Voorbeeld 1 vind je de posttarieven van 2007.
-
Bepaal `T(15)`.
-
Als je weet hoe zwaar een brief is, weet je voor hoeveel euro aan postzegels je er op moet plakken. Klopt dat? Leg uit.
-
Als je ziet voor hoeveel euro aan postzegels er op een brief zit, weet je hoe zwaar hij is. Klopt dat? Leg uit.
-
Welke oplossingen heeft de vergelijking: `T(G) = 1,32`?
-
Is `G` een functie van `T`? Verklaar je antwoord.
-
In Voorbeeld 1 en Voorbeeld 2 kun je zien wanneer een verband tussen twee variabelen een functie is. Bij welke van deze grafieken is `y` een functie van `x`?
A - 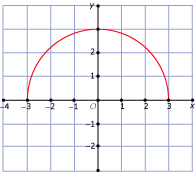 B -
B - 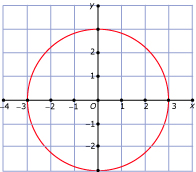
C - 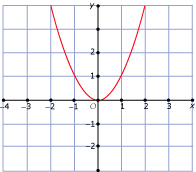 D -
D - 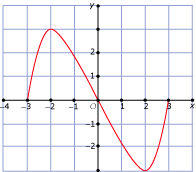
-
Bekijk in Voorbeeld 3 waarom het berekenen van nulpunten voordat je de functie in beeld brengt op je grafische rekenmachine belangrijk is.
Gegeven zijn de functies `f(x) = x^2 - 130` en `g(x) = 3x`.
-
Breng de grafieken van `f` en `g` in beeld met de standaardinstellingen voor het venster van je grafische rekenmachine.
Krijg je veel te zien?
-
Bereken de nulpunten van de grafiek van `f`. De grafiek van `f` is een parabool, wat is de top van deze parabool?
-
Pas je vensterinstellingen zo aan, dat deze punten nog in beeld komen. Schrijf de bijbehorende instellingen op.
-
Breng nu ook de grafiek van g in beeld. Hoeveel snijpunten hebben beide grafieken?
-
Bepaal met je grafische rekenmachine de snijpunten van beide grafieken. Bereken deze snijpunten ook algebraïsch.
-
Gegeven de functies `y_1=(x^2-4)(x^2-9)` en `y_2=-x^2-x+6`.
-
Bereken van beide functies de nulpunten.
-
Breng nu beide grafieken in beeld.
Schrijf op welke vensterinstellingen je gebruikt om alle nulpunten en toppen in beeld te krijgen.
-
Bepaal alle snijpunten van beide functies in twee decimalen nauwkeurig.
Verwerken
-
Gegeven is de functie `f(x) = 8 - 4x + x^3`.
-
Bereken `f(3)`.
-
Bereken de `x`-waarden waarvoor `f(x) = 8`.
-
Bij welke vensterinstellingen krijg je de nulpunten en de toppen van de grafiek van `f` in beeld?
-
Hoort bij elke waarde van `x` precies één waarde van `y`? Of kun je tegenvoorbeelden vinden?
-
Hoort bij elke waarde van `y` precies één waarde van `x`? Of kun je tegenvoorbeelden vinden?
-
Voor het gebruik van water betaal je jaarlijks € 42,00 en nog € 0,25 per verbruikte m3 water.
De jaarlijkse kosten `K` hangen af van het aantal m3 (`a`) dat je verbruikt.
-
Waarom is `K` een functie van `a`?
-
Bereken `K(100)`.
-
Stel het functievoorschrift `K(a)` op.
-
De meeste gezinnen betalen minder dan 500 euro per jaar voor hun waterverbruik.
Hoeveel kubieke meter water gebruiken die gezinnen op zijn hoogst?
-
Gegeven zijn de functies `f(x) = 100 - x^2` en `g(x) = x^2`.
-
Bereken de nulpunten en de top van de grafiek van `f`.
-
Breng de grafieken van `f` en `g` in beeld met je grafische rekenmachine.
Schrijf op bij welke vensterinstellingen de nulpunten en toppen van beide functies goed zichtbaar zijn.
-
Bereken in twee decimalen nauwkeurig de snijpunten van beide grafieken.
-
Gegeven de functies `y_1 = x^4 - 2x^2` en `y_2 = -x^2 + 4x`.
-
Bereken van beide functies de nulpunten.
-
Breng nu beide grafieken in beeld.
Schrijf op welke vensterinstellingen je gebruikt om alle nulpunten en toppen in beeld te krijgen.
-
Bepaal alle snijpunten van beide functies in één decimaal nauwkeurig.
-
Je ziet hier vier functievoorschriften. Bepaal telkens eerst de nulpunten van de grafiek. Schrijf vervolgens de vensterinstellingen op waarbij de grafiek goed in beeld komt.
-
`f(x) = 100x - x^2`
-
`g(x) = 10x(x - 50)`
-
`h(x) = (x - 10)^2 - 1600`
-
`k(x) = 200 + 1,6x`
Testen
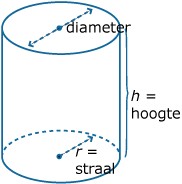
-
Voor de inhoud van een cilindervormig blikje geldt: `V = pi*r^2*h`.
Van een bepaalde serie blikjes is bekend dat de hoogte even groot is als de diameter.
Ze passen dus precies in een kubus.
-
Voor deze serie blikjes is `V` een functie van `r`.
Schrijf het bijpassende functievoorschrift op.
-
Neem aan dat 0 < r < 20.
Breng nu de grafiek van de functie `V(r)` in beeld. Schrijf de geschikte vensterinstellingen op.
-
Bij welke afmetingen van de cilinder geldt: `V = 1000` cm3?
-
Je ziet hier drie grafieken in het `Oxy`-assenstelsel van een grafische rekenmachine.
A - 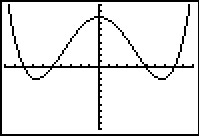 B -
B - 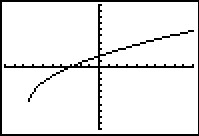 C -
C - 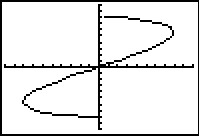
-
Bij welke van deze grafieken is `y` een functie van `x`?
-
Bij welke van deze grafieken is `x` een functie van `y`?
-
Gegeven zijn de functies `f(x) = 2x(x - 10)^2` en `g(x) = 8x`.
-
Bereken `f(5)` en `f(-5)`.
-
Bepaal de nulwaarden van `f`.
Schrijf op bij welke vensterinstellingen de grafieken van beide functies goed in beeld komen.
-
Bepaal de snijpunten van beide grafieken.
 Is y een functie van x bij formule 1?
Is y een functie van x bij formule 1?








 Is y een functie van x bij formule 1?
Is y een functie van x bij formule 1?

 B -
B - 
 D -
D - 
