
Het begrip functie
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Het begrip functie > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Het begrip functie > Inleiding
Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Het begrip functie > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Het begrip functie > Uitleg
Opgaven
-
Bekijk de eerste pagina van de Uitleg.
Voor de windmolen met wieken van 10 m geldt `P(v) = 0,052v^3`.
Daarin is `P` het vermogen in kW en `v` de windsnelheid in m/s.
-
Bereken `P(6)` betekent:
A - Bereken de functiewaarde bij invoerwaarde `v = 6`.
B - Bereken de invoerwaarde bij functiewaarde `v = 6`.
C - Bereken de functiewaarde als `P = 6`.
D - Bereken de invoerwaarde als `P = 6`.
- Bereken `P(6)`.
Bekijk nu de tweede pagina van de Uitleg.
-
Windsnelheden van 0 tot 15 m/s komen in de kustgebieden regelmatig voor.
Breng het deel van de grafiek van `P` dat daarbij hoort in beeld op je grafische rekenmachine.
Welke waarden voor `P` horen daar bij?
-
Voor welke waarde van `v` geldt: `P(v) = 300`? Licht het antwoord toe.
-
Neem nu een windmolen met wieklengte 20 m.
-
Welk voorschrift geldt nu voor `P` als functie van `v`?
-
Bereken `P(10)`.
-
Breng de grafiek in beeld voor windsnelheden vanaf 0 tot en met 20 m/s.
Welke vensterinstellingen heb je nodig om de complete grafiek in beeld te krijgen?
-
Bij welke windsnelheid in km/h is het vermogen 40 kW?
-
Bekijk de derde pagina van de Uitleg.
-
Geef nog een voorbeeld waaruit blijkt dat de formule `x^2 + y^2 = 100` geen functievoorschrift is.
-
Schrijf deze formule in de vorm `y =` ...
-
Door welke twee functievoorschriften `y_1` en `y_2` kun je de formule vervangen?
-
Breng nu de grafieken van deze twee functies in beeld. Welke vensterinstellingen gebruik je?
-
Bereken `y_1(5)` en `y_2(5)`.
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Het begrip functie > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Het begrip functie > Theorie
Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.
Opgaven
-
Gegeven is de functie `f` met voorschrift `f(x)=x^2-4x`.
Welke van deze uitspraken zijn waar?
A - `f(4)` is een invoerwaarde
B - `f(10) = 60` betekent dat het punt (60;10) op de grafiek ligt.
C - `f(x) = 5` heeft twee oplossingen.
D - Bij elke waarde van x hoort precies één waarde van y.
-
Bekijk nog eens de functie `f` met voorschrift `f(x)=x^2-4x`.
-
Bereken de nulwaarden van `f`.
-
Welke nulpunten heeft de grafiek van `f`?
-
Los op: `f(x)=5`.
-
In Voorbeeld 1 vind je de posttarieven van 2007.
-
Bepaal `T(15)`.
-
Als je weet hoe zwaar een brief is, weet je voor hoeveel euro aan postzegels je er op moet plakken. Klopt dat? Leg uit.
-
Als je ziet voor hoeveel euro aan postzegels er op een brief zit, weet je hoe zwaar hij is. Klopt dat? Leg uit.
-
Welke oplossingen heeft de vergelijking: `T(G) = 1,32`?
-
Is `G` een functie van `T`? Verklaar je antwoord.
-
In Voorbeeld 1 en Voorbeeld 2 kun je zien wanneer een verband tussen twee variabelen een functie is. Bij welke van deze grafieken is y een functie van x?
A - 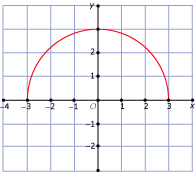 B -
B - 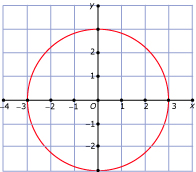
C - 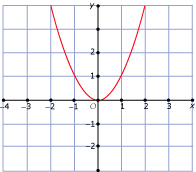 D -
D - 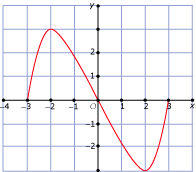
-
Bekijk in Voorbeeld 3 waarom het berekenen van nulpunten voordat je de functie in beeld brengt op je grafische rekenmachine belangrijk is.
Gegeven zijn de functies `f(x) = x^2 - 130` en `g(x) = 3x`.
-
Breng de grafieken van `f` en `g` in beeld met de standaardinstellingen voor het venster van je grafische rekenmachine.
Krijg je veel te zien?
-
Bereken de nulpunten van de grafiek van `f`. De grafiek van `f` is een parabool, wat is de top van deze parabool?
-
Pas je vensterinstellingen zo aan, dat deze punten nog in beeld komen. Schrijf de bijbehorende instellingen op.
-
Breng nu ook de grafiek van g in beeld. Hoeveel snijpunten hebben beide grafieken?
-
Bepaal met je grafische rekenmachine de snijpunten van beide grafieken. Bereken deze snijpunten ook algebraïsch.
-
Gegeven de functies `y_1=(x^2-4)(x^2-9)` en `y_2=-x^2-x+6`.
-
Bereken van beide functies de nulpunten.
-
Breng nu beide grafieken in beeld.
Schrijf op welke vensterinstellingen je gebruikt om alle nulpunten en toppen in beeld te krijgen.
-
Bepaal alle snijpunten van beide functies in twee decimalen nauwkeurig.
Verwerken
-
Gegeven is de functie `f(x) = 8 - 4x + x^3`.
-
Bereken `f(3)`.
-
Bereken de `x`-waarden waarvoor `f(x) = 8`.
-
Bij welke vensterinstellingen krijg je de nulpunten en de toppen van de grafiek van `f` in beeld?
-
Hoort bij elke waarde van `x` precies één waarde van `y`? Of kun je tegenvoorbeelden vinden?
-
Hoort bij elke waarde van `y` precies één waarde van `x`? Of kun je tegenvoorbeelden vinden?
-
Voor het gebruik van water betaal je jaarlijks € 42,00 en nog € 0,25 per verbruikte m3 water.
De jaarlijkse kosten `K` hangen af van het aantal m3 (`a`) dat je verbruikt.
-
Waarom is `K` een functie van `a`?
-
Bereken `K(100)`.
-
Stel het functievoorschrift `K(a)` op.
-
De meeste gezinnen betalen minder dan 500 euro per jaar voor hun waterverbruik.
Hoeveel kubieke meter water gebruiken die gezinnen op zijn hoogst?
-
Gegeven zijn de functies `f(x) = 100 - x^2` en `g(x) = x^2`.
-
Bereken de nulpunten en de top van de grafiek van `f`.
-
Breng de grafieken van `f` en `g` in beeld met je grafische rekenmachine.
Schrijf op bij welke vensterinstellingen de nulpunten en toppen van beide functies goed zichtbaar zijn.
-
Bereken in twee decimalen nauwkeurig de snijpunten van beide grafieken.
-
Gegeven de functies `y_1 = x^4 - 2x^2` en `y_2 = -x^2 + 4x`.
-
Bereken van beide functies de nulpunten.
-
Breng nu beide grafieken in beeld.
Schrijf op welke vensterinstellingen je gebruikt om alle nulpunten en toppen in beeld te krijgen.
-
Bepaal alle snijpunten van beide functies in één decimaal nauwkeurig.
-
Je ziet hier vier functievoorschriften. Bepaal telkens eerst de nulpunten van de grafiek. Schrijf vervolgens de vensterinstellingen op waarbij de grafiek goed in beeld komt.
-
`f(x) = 100x - x^2`
-
`g(x) = 10x(x - 50)`
-
`h(x) = (x - 10)^2 - 1600`
-
`k(x) = 200 + 1,6x`
Testen
-
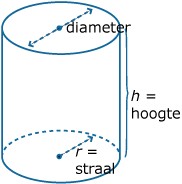
Voor de inhoud van een cilindervormig blikje geldt: `V = pi*r^2*h`.
Van een bepaalde serie blikjes is bekend dat de hoogte even groot is als de diameter.
Ze passen dus precies in een kubus.
-
Voor deze serie blikjes is `V` een functie van `r`.
Schrijf het bijpassende functievoorschrift op.
-
Neem aan dat 0 < r < 20.
Breng nu de grafiek van de functie `V(r)` in beeld. Schrijf de geschikte vensterinstellingen op.
-
Bij welke afmetingen van de cilinder geldt: `V = 1000` cm3?
-
Je ziet hier drie grafieken in het `Oxy`-assenstelsel van een grafische rekenmachine.
A - 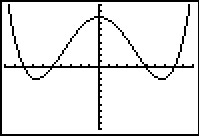 B -
B - 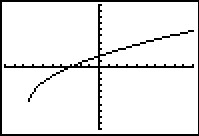 C -
C - 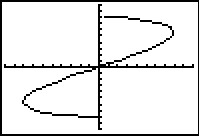
-
Bij welke van deze grafieken is `y` een functie van `x`?
-
Bij welke van deze grafieken is `x` een functie van `y`?
-
Gegeven zijn de functies `f(x) = 2x(x - 10)^2` en `g(x) = 8x`.
-
Bereken `f(5)` en `f(-5)`.
-
Bepaal de nulwaarden van `f`.
Schrijf op bij welke vensterinstellingen de grafieken van beide functies goed in beeld komen.
-
Bepaal de snijpunten van beide grafieken.

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Het begrip functie > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Het begrip functie > Inleiding
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Het begrip functie > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Het begrip functie > Uitleg
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Het begrip functie > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Het begrip functie > Theorie
 B -
B - 
 D -
D - 
