
Vergelijkingen
Inleiding
Een architect wil een goede trap ontwerpen. Hij gebruikt daarvoor de formule:
2 · optrede + aantrede = paslengte
Hij gaat uit van een paslengte van 70 cm.
Voor de optrede wil hij 16 cm nemen.
Vult hij deze gegevens in de formule in, dan krijgt hij de vergelijking: 32 + aantrede = 70.
Hij kan dus als aantrede nemen: aantrede = 70 – 32 = 38 cm.
Op deze manier heeft hij de vergelijking opgelost.
Het getal 38 maakt de vergelijking kloppend: 32 + 38 = 70.
Je leert nu:
- systematisch vergelijkingen met één variabele oplossen met al bekende oplossingsmethoden;
- vergelijkngen oplossen met de grafische rekenmachine.
Je kunt al:
- werken met variabelen (met 'letters');
- eenvoudige algebraïsche technieken zoals terugrekenen, de balansmethode bij vergelijkingen en werken met haakjes.
Verkennen
Je hebt al in voorgaande jaren vergelijkingen opgelost.
> Zet even je kennis op een rijtje: welke soorten vergelijkingen ken je en welke oplossingsmethoden ken je?
> Een zuiver rechthoekig doosje met een vierkante bodem en een hoogte van 12 cm heeft een buitenoppervlakte (inclusief bodem en deksel) van 512 cm2. Welke afmetingen heeft dat doosje?
Beantwoord deze vraag met behulp van een vergelijking.
Theorie
Formules zoals y = 2x + 3, of a + 4b – c = 15, of 6x + 10 = 2x – 8 noem je vergelijkingen. Je kunt dan waarden (of combinaties van waarden) zoeken die de vergelijking kloppend maken, dat heet het oplossen van een vergelijking.
Vergelijkingen kun je systematisch oplossen door herschrijven.
Vooral bij vergelijkingen met één variabele doe je dat vaak.
Je gebruikt dan algebraïsche methoden, zoals:
- de balansmethode, waarbij je aan beide zijden van het is-gelijk-teken
- hetzelfde optelt of aftrekt;
- met hetzelfde vermenigvuldigt of door hetzelfde deelt (maar niet 0).
- de terugrekenmethode, waarbij je bewerkingen ongedaan maakt door het tegenovergestelde te doen:
- optellen maak je ongedaan door aftrekken (en omgekeerd);
- vermenigvuldigen maak je ongedaan door delen (en omgekeerd);
- machten maak je ongedaan door worteltrekken (en omgekeerd).
- ontbinden in factoren, waarbij je gebruik maakt van het feit dat een vergelijking van de vorm a · b = 0 gelijkwaardig is met a = 0 V b = 0.
Het teken V betekent dat je deze uitdrukking moet lezen als a = 0 en/of b = 0 (dus a = 0 of b = 0 of beide).
Als algebraïsche methoden niet werken, kun je nog
denken aan inklemmen: je zoekt dan door proberen op een steeds kleiner
zoekgebied. Je grafische rekenmachine heeft daar diverse routines voor ingebouwd.
‡
Voorbeeld 1
Los de vergelijking `1/2 (x+8) = -7+x` op met de balansmethode.
Antwoord
Haakjes uitwerken: `1/2 x+4 = -7+x` beide zijden –4
`1/2 x = -11 + x` beide zijden –x
`-1/2 x = -11` beide zijden vermenigvuldigen met –2
`x=22`
Je kunt dit antwoord nog controleren door aan beide zijden van de gegeven vergelijking voor x het getal 22 te substitueren.
‡
Voorbeeld 2
In de vergelijking 2(x – 4)2 = 32 komt de onbekende x maar op één plek voor. Je kunt hem oplossen met terugrekenen.
Antwoord
Eerst even uitzoeken hoe je heen rekent vanuit x:
x  32
32
Vervolgens ga je terugrekenen:
x 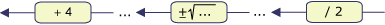 32
32
Je vindt: `x=+-sqrt(32/2)+4` en dus x = 0 V x = 8
En weer controleren door invullen!
‡
Voorbeeld 3
Deze twee vergelijkingen kun je oplossen met ontbinden in factoren:
- `x^2-5x+6=0`
- `x^3=4x`
Antwoord
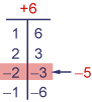
De eerste vergelijking gaat zo:
`x^2-5x+6=0`
`(x-2)(x-3)=0`
`x-2=0 vv x-3=0`
`x=2 vv x=3 `
En de tweede vergelijking gaat zo:
`x^3=4x`
`x^3-4x=0`
`x(x^2 -4)=0`
`x=0 vv x^2 -4=0`
`x=0 vv x^2 =4`
`x=0 vv x=-2 vv x=2`
‡
Voorbeeld 4
De vergelijking `x+x^2=10` kun je oplossen met inklemmen.
Antwoord
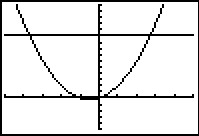
Eerst maak je de grafieken van y1 = x + x2 en y2 = 10 op de grafische rekenmachine. Breng ze zo in beeld dat alle snijpunten zichtbaar zijn!
De grafieken snijden elkaar tweemaal. De vergelijking heeft twee oplossingen.
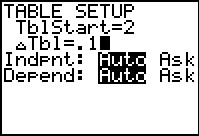
Voor de positieve oplossing moet je zoeken tussen 2 en 3. Stel de tabel in op stappen (voor x) van 0,1.
Je ziet dat je verder moet zoeken tussen 2,7 en 2,8.
Het zoekgebied wordt kleiner, je klemt de oplossing in.
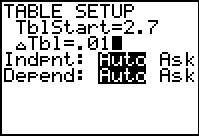
Stel vervolgens een stapgrootte van 0,01 in en zoek tussen 2,70 en 2,80.
Nu zie je dat de oplossing tussen 2,70 en 2,71 ligt, het dichtst bij 2,70.
Zo vind je op twee decimalen nauwkeurig: x ≈ 2,70.
Als een nauwkeuriger oplossing wordt verlangd, moet je nog door zoeken tussen 2,700 en 2,710.
Op dezelfde manier bepaal je de andere oplossing.
Op twee decimalen nauwkeurig is de volledige oplossing: x ≈ 2,70 V x ≈ –3,70.
‡
Voorbeeld 5
Los de vergelijking `1/x + 2/(x+3) = 1` zowel algebraïsch als met de grafische rekenmachine op.
Antwoord
De oplossing met de grafische rekenmachine is betrekkelijk eenvoudig:
- Voer in: Y1=1/X+2/(X+3) en Y2=3.
- Bekijk de grafieken.
- Je vindt de twee x-waarden waar Y1 en Y2 gelijk zijn in de tabel, maar exacte waarden vind je niet.
De algebraïsche oplossing gaat bijvoorbeeld zo:
`1/x + 2/(x+3) = (x+3)/(x(x+3)) + (2x)/(x(x+3)) = (3x+3)/(x(x+3)) = 1`
en dus: 3x + 3 = x(x + 3). (Let op dat zowel x ≠ 0 als x + 3 ≠ 0 moet zijn!)
Dit geeft: x2 = 3 en dus `x=sqrt(3) vv x=-sqrt(3)`.
Je ziet meteen hoe nuttig algebraïsche methoden zijn: je vindt meteen de exacte oplossingen, terwijl je je anders moet behelpen met benaderingen, die vaak nog lastig te vinden zijn ook...
‡
Opgaven
-
Bekijk Voorbeeld 1.
Los de volgende vergelijkingen op met de balansmethode.
-
`3t - 400 = 700`
-
`3t - 400 = 700 - 2t`
-
`2300 - 0,15 * p = 1600 + 0,42 * p`
-
Bekijk Voorbeeld 2.
Los de volgende vergelijkingen op door terugrekenen.
-
`3t - 400 = 700`
-
`(3 * t - 20)^2 = 1600`
-
`3 * p^3 = 81`
-
Bekijk Voorbeeld 3.
Los de volgende vergelijkingen op door ontbinden in factoren.
-
`0,5x^2 = 4x`
-
`k^2 + 5k - 6 = 0`
-
`8p - p^2 = 0`
-
`x(x - 2) = 3x - 6`
-
`x^2 = x + 12`
-
`x^3 = 4x`
-
Niet alle vergelijkingen kun je met de balansmethode, door terugrekenen of ontbinden in factoren systematisch oplossen. De oplossing vinden door inklemmen werkt daarentegen wel altijd. Je moet dan van tevoren een idee hebben van het zoekgebied, dus van het gebied waarin de oplossing is te vinden. In Voorbeeld 4 kun je nalezen hoe je de inklemmethode gebruikt samen met je grafische rekenmachine.
Los de volgende vergelijkingen op met de inklemmethode. Geef je oplossingen in drie decimalen nauwkeurig.
-
`x^3 = 4 - x`.
-
`600/a = 18 + 0,04a`
-
Los de volgende vergelijkingen op met de grafische rekenmachine. Geef waar nodig benaderingen in twee decimalen nauwkeurig.
-
`x^3 + 2x = 16`
-
`x + sqrt(x) = 10`
-
`l + 10/l = 10`
-
`300/(p+4)=20`
-
Bekijk Voorbeeld 5.
Los de volgende vergelijkingen zowel algebraïsch als met de grafische rekenmachine op.
-
`1/(x+3)+1/x=1/2`
-
`20/(p^2+5)=2`
-
`10/x+1=5/x`
Verwerken
-
Los de volgende vergelijkingen algebraïsch op.
-
`4t + 50 = 200`
-
`4t^2 + 50 = 200`
-
`sqrt(x+4)=20`
-
`(2x - 5)^3 = 125`
-
`sqrt(a^2+4)-20=0`
-
`12/v=400`
-
`2x^2 - 2 = 12x + 30`
-
Los de volgende vergelijkingen op door inklemmen met behulp van je grafische rekenmachine. Zoek alle oplossingen.
-
`sqrt(x)=6-x`
-
`x^4=2+x`
 Het Empire State Building is een hoge wolkenkrabber in New York. Stel je voor dat iemand van het 381 m hoge gebouw een steentje laat vallen!
Het Empire State Building is een hoge wolkenkrabber in New York. Stel je voor dat iemand van het 381 m hoge gebouw een steentje laat vallen!
Onder invloed van de zwaartekracht valt een steen eenparig versneld (de luchtweerstand laat je buiten beschouwing). Natuurkundigen hebben daarvoor een rekenmodel bedacht. Daarin hangen de afgelegde weg `s` (in meter) en de snelheid `v` (in m/s) af van de tijd `t` (in seconde) volgens de formules `s = 4,9t^2` en `v = 9,8t`.
-
Geef een formule voor de hoogte `h` van het steentje boven de grond als functie van `t`.
-
Bereken het tijdstip waarop het steentje op de grond komt.
-
Bereken de snelheid waarmee het steentje op de grond komt. Geef je antwoord zowel in m/s als in km/h.
-
Bereken bij deze formules de waarde van de éne variabele als de andere 0 is.
-
`2p - 3q = 650`
-
`W = -0,25q(0,5q - 100)`
-
`k^2 + (l + 2)^2 = 100`
-
`a = 1200/(600+0,2d^2) - 1`
-
`(x^2 - 4)(y^2 - 9) = -36`
-
`y^4 + 1 = 4/(1+x^2)`
-
Een boer wordt door de gemeente gevraagd om een stuk land te voorzien van een boswal van 4 m breedte. Het stuk land is zuiver vierkant. Het grenst aan één kant al aan het bos, zodat er maar aan driekanten een strook af hoeft voor de boswal. "Ik houd zo maar de helft van mijn land over", verzucht de boer.
Als dat waar is, hoe groot is dan de oppervlakte van het land?
Los dit probleem op met behulp van een vergelijking.
-
Sommige kaarsen zijn bijna zuiver cilindervormig. Stel je voor dat je zo’n kaars wilt maken met een lengte van 20 cm. Je neemt een lont met een diameter van 3 mm en dompelt die een aantal keer in een bad met vloeibaar kaarsvet. Elke onderdompeling wordt de diameter van de kaars 1 mm groter. De hoeveelheid kaarsvet `V` in de kaars hangt af van het aantal onderdompelingen `a`.
-
Geef een formule voor `V` als functie van `a`.
-
Breng de grafiek van deze functie met je grafische rekenmachine in beeld.
-
Na hoeveel onderdompelingen is de hoeveelheid kaarsvet in de kaars ongeveer 106 cm3?
Lees je antwoord eerst uit de grafiek af en bereken het daarna door de bijbehorende vergelijking algebraïsch op te lossen.
Testen
-
Los de volgende vergelijkingen algebraïsch op.
-
`1,25t + 5,50 = 1,85t`
-
`0,15(p - 2)^2 = 1,35`
-
`12 - sqrt(4+x^2) = 0`
-
`3g^2 - 6g = 360`
-
Los de volgende vergelijkingen op door inklemmen met behulp van je grafische rekenmachine.
(Eventuele benaderingen in één decimaal nauwkeurig.)
-
`0,12q + 600/q = 30`
-
`4/(sqrt(3+x^2))=1/x`
-
Los deze vergelijking algebraïsch op: `2/(x+1)+1/x=0`
-
Voor de totale oppervlakte `A` van een cilindervormig groenteblik met straal `r` en hoogte `h` geldt: `A = 2pi r^2 + 2pi rh`.
-
Leg uit hoe je deze formule zelf kunt afleiden.
-
Bereken in cm3 nauwkeurig de oppervlakte van een groenteblik met een diameter van 20 cm en een hoogte van 30 cm.
-
Een groenteblik met een oppervlakte van 1000 cm2 heeft een hoogte van 20 cm. Bereken de diameter in mm nauwkeurig.
-
Van een groenteblik met een oppervlakte van 1000 cm2 zijn de hoogte en de diameter even groot.
Bereken de diameter in mm nauwkeurig.
 32
32

 32
32
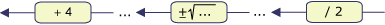 32
32



