Totaalbeeld

Samenvatten

Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Oppervlakte en inhoud. Een eigen samenvatting maken is nuttig.

Begrippenlijst:

21: oppervlakte van een vlakke figuur — oppervlakteformules van rechthoek, driehoek, parallellogram, trapezium, cirkel
22: oppervlakte van een lichaam — oppervlakteformule van een bol
23: inhoud van een lichaam — inhoudsformules van prisma, cilinder, piramide, kegel, bol
24: schaalvergroting — lengte-, oppervlakte- en inhoudvergrotingsfactor

Activiteitenlijst:

21: de oppervlakte van de meeste vlakke figuren berekenen m.b.v. de oppervlakteformules
22: de oppervlakte van veel lichamen berekenen
23: de inhoud van veel lichamen berekenen
24: verband tussen lengte-, oppervlakte- en inhoudvergrotingsfactor toepassen

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Totaalbeeld > Achtergronden

Testen

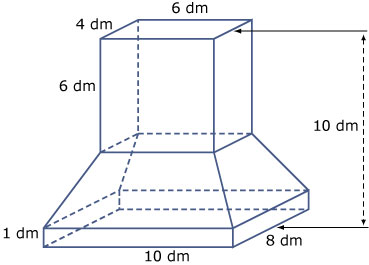  1. Je ziet hier een stalen afzuigkap in een grote keuken. Het bovenste deel is een balk, het onderste gedeelte ook. De vier schuine vlakken hebben allemaal de vorm van een symmetrisch trapezium.
    1. Bereken de totale inhoud van deze afzuigkap.
    2. Bereken de totale oppervlakte van deze afzuigkap.

  2. Een plastic koffiebekertje heeft (ongeveer) de vorm van een afgeknotte kegel. Van een bepaald koffiebekertje is de diameter van de bodem 46 mm, die van de bovencirkel 64 mm en de hoogte 90 mm.
    Bereken de inhoud van dit koffiebekertje en bereken de oppervlakte aan plastic.

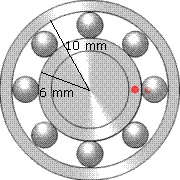  3. Je ziet hier een doorsnede van een kogellager. In je fiets zit om de as van elk wiel zo’n kogellager om ervoor te zorgen dat de draaibeweging van elk wiel met weinig wrijving kan worden uitgevoerd. De kogeltjes van dit lager zijn zuivere bollen en hebben een diameter van 4 mm. De kogeltjes zitten in een cilindervormige ring met een buitenstraal van 10 mm en een binnenstraal van 6 mm. De hoogte van die ring is gelijk aan de diameter van elk kogeltje. De ruimte tussen de kogeltjes is opgevuld met vet.
    Hoeveel % van de inhoud van de ring waarbinnen de kogeltjes zitten bestaat uit vet?

  4. In een cilindervormige koker passen precies drie tennisballen boven elkaar.
    Hoeveel % van de inhoud van de koker bestaat uit lucht?

  5. IKEA heeft weer een nieuwe plastic fruitbak op de markt. Je ziet hem hier. Hij bestaat uit een massieve cilinder met een diameter van 40 cm en een hoogte van 41 cm waaruit een afgeknotte kegel is weg geboord. De bodem van deze afgeknotte kegel is 1 cm dik en de diameter van de grondcirkel van de afgeknotte kegel is 30 cm. De vaas is behoorlijk zwaar hoewel de soortelijke massa van het plastic maar 0,5 gram/cm3 is.
    1. Bereken de hoeveelheid plastic van de bak in cm3 nauwkeurig.
    2. Bereken het gewicht van de bak in grammen nauwkeurig.

  6. Een regelmatige vierzijdige piramide van hout wordt evenwijdig aan het grondvlak doorgezaagd. De oorspronkelijke hoogte van de piramide was 12 cm, het afgezaagde topje (ook een piramide) heeft een hoogte van 8 cm. Je hebt nu twee nieuwe ruimtelijke objecten: het afgezaagde topje en de onderkant (een afgeknotte piramide). Hoe verhouden zich hun gewichten?

  7. Het lichaam `ABC.DEF` past in een balk van 4 bij 4 bij 6 dm. Punt `D` ligt op 3 dm hoogte en punt `E` op 2 dm hoogte.

        

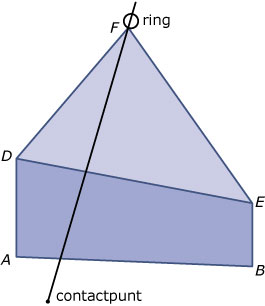
    1. Bereken de inhoud van het lichaam `ABC.DEF`.
    2. Teken een uitslag van het lichaam `ABC.DEF`.
    In het punt `F` bevindt zich een draaibare ring. Door deze ring wordt een stang gestoken. Deze stang rust op ribbe `DE` en wordt doorgeschoven totdat het uiteinde de grond raakt. Bij verschillende standen van de stang horen verschillende contactpunten met de grond.
    1. Teken in de uitslag het lijnstuk dat wordt gevormd door alle mogelijke contactpunten.
    2. Punt `P` is het contactpunt dat het dichtst bij `F` ligt. Onderzoek door berekening of een stang met een lengte van 75 cm lang genoeg is om `F` en `P` te verbinden.

Toepassen

  1. De Meeh-coëfficiënt

    De Duitse bioloog Carl Meeh legde een verband tussen het lichaamsgewicht en de huidoppervlakte bij dieren. Daarbij gebruikte hij de Meeh-coëfficiënt. Door het gewicht van een massieve kubus of bol met zijn buitenoppervlakte te vergelijken kun je afleiden welk type formule daar bij past. Lees hierover via

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Totaalbeeld > Toepassen


    Bekijk nu een massieve kubus, een massieve bol en een massieve cilinder. Alle drie zijn ze gemaakt van materiaal dat 1,5 gram/cm3 weegt. Het gewicht noem je `G` en de buitenoppervlakte `H`.
    1. Bereken `G` en `H` van een kubus met ribben van `r` cm.
      Stel een formule op voor `H` uitgedrukt in `G`.
    2. Bereken `G` en `H` van een bol met een straal van `r` cm.
      Stel een formule op voor `H` uitgedrukt in `G`.
    3. Bereken `G` en `H` van een cilinder met een straal van `r` cm en een hoogte van `r` cm.
      Stel een formule op voor `H` uitgedrukt in `G`.
    4. Welke Meeh-coëfficiënten hebben deze kubus, deze bol en deze cilinder?

Examenopgaven

  1. Voetstuk

    Een pijler onder een brug rust op een betonnen voetstuk. Het voetstuk staat op de grond en bestaat uit twee delen. Het onderste deel heeft de vorm van een balk, het bovenste deel `ABCD.EFGHKLMN` zorgt voor de overgang naar de pijler die achtzijdig is. Zie de linker figuur. De rechter figuur is een vooraanzicht van het voetstuk. In beide figuren zijn de afmetingen gegeven in centimeters.

        

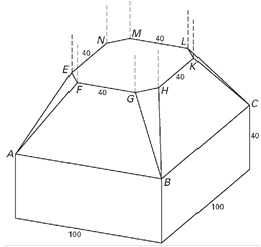
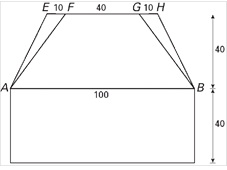
    1. Met behulp van dit vooraanzicht kan de hoek berekend worden die het schuine vlak `BCKH` met het vlak `ABCD` maakt. Bereken die hoek. Rond je antwoord af op gehele graden.
    2. Teken een bovenaanzicht van dit voetstuk op schaal 1:10. Zet de letters erbij.
    Er wordt een lint evenwijdig aan vlak `ABCD` om het voetstuk gespannen. Het lint is 500 cm lang. Als het lint om het balkgedeelte wordt gespannen, is er 100 cm over. Gaat het lint door de punten `E`, `F`, `G`, `H`, `K`, `L`, `M` en `N`, dan is er ongeveer 283 cm over.
    1. Toon met een berekening aan dat er dan inderdaad ongeveer 283 cm over is.
    2. Het lint wordt nu op een hoogte van 50 cm (gerekend vanaf de grond) om het voetstuk gespannen. Bereken hoeveel cm van het lint op deze hoogte over is. Rond je antwoord af op een geheel getal.
    Het gedeelte van het voetstuk tussen de vlakken `ABCD` en `EFGHKLMN` wordt geschilderd: de vier vierhoekige zijvlakken worden rood en de vier driehoekige zijvlakken worden zwart. Om te weten hoeveel verf nodig is, moet men de oppervlakte weten.
    1. Bereken de totale oppervlakte van de delen die rood geschilderd worden. Rond je antwoord af op gehele cm2.

    (bron: examen wiskunde B1,2 havo 2003, opgave 1)


  2. Koffiefilter en koffiefilterhouder

    In platgedrukte toestand (in de verpakking) heeft een filterzakje een vorm die ontstaat door uit een cirkelsector `DMC` de gelijkbenige driehoek `AMB` weg te laten (bekijk de figuren hieronder). We gaan uit van de volgende afmetingen: `AB = 6` cm, `MB = 4,8` cm en `BC = 10,5` cm. Plakrandjes laten we buiten beschouwing.

        

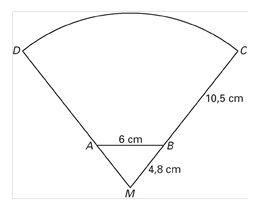
    1. `/_CMD` is, afgerond op een geheel aantal graden, gelijk aan 77°. Toon dat aan.
    2. Een koffiefilter (zie figuur) wordt opengeknipt langs de zijden `CB` en `BA` en daarna opengevouwen om de zijde `AD`. Zo ontstaat er een uitslag van het koffiefilter. Teken deze uitslag op schaal 1:3.
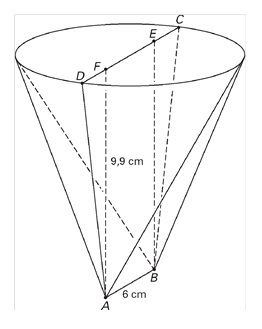
    In de figuur hiernaast is een model van een koffiefilterhouder getekend. De hoogte `AF` is 9,9 cm. De onderkant is het lijnstuk `AB` met een lengte van 6 cm. De bovenrand van de houder heeft de vorm van een cirkel.
    Een filter wordt opengevouwen in de koffiefilterhouder geplaatst. We nemen aan dat daarbij de bovenste rand van het filter precies samenvalt met de bovenste rand van de filterhouder. De afstand tussen de punten `C` en `D` van het filter wordt bij het openvouwen natuurlijk kleiner.
    1. Bereken de middellijn `CD` van de filterhouder. Geef je antwoord in centimeters, afgerond op één decimaal.
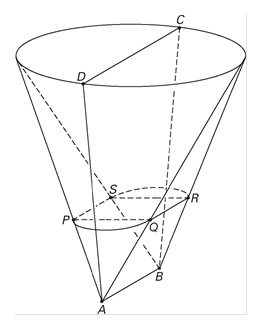
    In de figuur hiernaast is op een bepaalde hoogte de dwarsdoorsnede van de koffiefilterhouder getekend. Deze dwarsdoorsnede is een figuur die bestaat uit een rechthoek `PQRS` en twee halve cirkels met middellijnen `PQ` en `RS`. We nemen aan dat `CD` exact gelijk is aan 13 cm.
    Hieronder zijn (op schaal) parallelle doorsneden getekend van de houder op 0%, 25%, 50%, 75% en 100% van de hoogte.



    1. Bereken de oppervlakte van de dwarsdoorsnede op eenderde deel van de hoogte. Geef je antwoord in cm2.

    (bron: examen wiskunde B1,2 havo 2004)


  3. Kaas

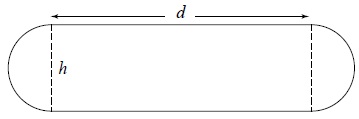
    Op de foto hieronder zie je drie stukken kaas. Het zijn delen van een hele, ronde kaas. Het grootste stuk is precies de helft van een hele kaas. Deze halve kaas heeft een vlakke zijkant. De vorm van de vlakke zijkant bestaat bij benadering uit een rechthoek van 30 cm bij 10 cm en twee halve cirkels met een diameter van 10 cm.

        

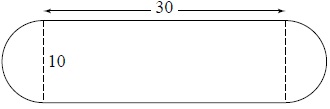
    1. Bereken de oppervlakte van de vlakke zijkant. Rond je antwoord af op een geheel aantal cm2.
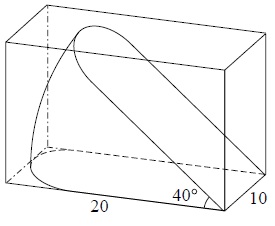    Als je verticaal door het midden van de kaas snijdt, kun je stukken kaas maken zoals die ook op de foto hierboven te zien zijn. Bij een van de stukken kaas op die foto maken de snijvlakken een hoek van 40° met elkaar. Zo'n stuk wordt met een snijvlak op de bodem van een balkvormig doosje gelegd. De binnenmaten van het grondvlak van het doosje zijn 20 cm bij 10 cm. Zie de figuur hiernaast.
    1. Bereken hoe hoog de binnenkant van dit doosje minimaal moet zijn om dit stuk kaas er in te laten passen. Geef je antwoord in een geheel aantal centimeters.
    Het volume van hele kazen die de vorm hebben van de kaas op de foto hierboven, kan worden berekend met behulp van de volgende formule:

    `V = 1/6pi h^3 + 1/8pi^2 dh^2 + 1/4pi d^2 h

    Hierin is `V` het volume in cm3, `h` is de hoogte van de kaas in cm en `d` is de zogeheten binnendiameter van de kaas in cm.



    Iemand wil kazen maken met deze vorm. Het volume van een hele kaas moet 5000 cm3 zijn en de hoogte moet 8 cm zijn. De kaas wordt gerijpt in een kamer van 3,50 m lang. Over de hele lengte van de kamer zijn planken tegen de muur aan gemaakt waarop de kazen naast elkaar kunnen liggen.
    1. Bereken hoeveel van deze kazen er maximaal naast elkaar op een plank kunnen liggen als ze worden neergelegd zoals de foto hiernaast.
    2. Als de binnendiameter 0 wordt, ontstaat een bolvormige kaas. De inhoud van deze bolvormige kaas kun je ook uitrekenen met bovenstaande formule van `V`. Vul `d = 0` in de formule van `V` in en werk de formule die hierbij ontstaat om tot de bekende formule voor de inhoud van een bol met straal `r`.

    (bron: herexamen wiskunde B havo 2009, opgave 1)