Totaalbeeld

Antwoorden bij de opgaven

    1. De kap bestaat uit een balk van 10 bij 8 bij 1, een balk van `6 + 3` bij 6 bij 4 en vier kwartpiramides die je kunt samenvoegen tot een piramide met grondvlak 4 bij 4 en hoogte 3. (Het middenstuk is geen afgeknotte piramide!)
      Inhoud `= 10 * 8 * 1 + (6 + 3) * 6 * 4 + 1/3 * 4 * 4 * 3 = 312` dm3.
    2. Opp `= 2 * 10 * 1 + 2 * 8 * 1 + 2 * 1/2 * (10 + 6) * sqrt(13) + 2 * 1/2 * (8 + 4) * sqrt(13) + 2 * 6 * 6 + 2 * 6 * 4 = 156 + 28 sqrt(13)` dm2.
  2. Het bekertje is een afgeknotte kegel, waarvan het weggehaalde deel een kegel is met een hoogte `h` waarvoor `h/(h + 90) = 46/64`. Daaruit volgt: `h = 230` mm.
    De inhoud van het bekertje is `1/3 * pi * 32^2 * 310 - 1/3 * pi * 23^2 * 230 ~~ 205010` mm3 en dat is ongeveer 205 cm3, dus 0,205 liter.
    De oppervlakte aan plastic is `pi * 32 * sqrt(32^2 + 310^2) - pi * 23 * sqrt(23^2 + 210^2) + pi * 23^2 ~~ 16290` mm2.
  3. `I(text(kogeltje)) = 4/3pi * 2^3 = 32/3pi`
    `I(text(ring)) = pi * 10^2 * 4 - pi * 6^2 * 4 = 256pi`
    `I(text(vet)) = 256pi - 8 * 32/3pi = 170 2/3 pi`
    Het percentage aan vet is `66 2/3`.
  4. De straal van een tennisbal is `r`. De drie ballen hebben dan samen een volume van `3 * 4/3 pi r^3 = 4pi r^3`.
    De koker heeft een volume van `pi r^2 * 6r = 6pi r^3`.
    Dus `2/6` deel is lucht, dat is `33 1/3`%.
    1. De binnenkant van de fruitbak is een afgeknotte kegel met een hoogte van 160 cm. De hoeveelheid plastic is `pi * 20^2 * 41 - (1/3 * pi * 20^2 * 160 - 1/3 * pi * 15^2 * 120) = 4066 2/3 pi ~~ 12776` cm3.
    2. Het gewicht is ongeveer 6388 gram.
  6. De hoogte van het bovenste deel van de piramide is `8/12 = 2/3` deel van de hele piramide. De inhoud van het bovenste deel is daarom `(2/3)^3 = 8/27` deel van de hele piramide. De gewichten van beide delen verhouden zich als 8 : 27.
    1. `1/2 * 4 * 4 * 2 + 1/3 * 10 * 4 = 29 1/3`
    2. Zie figuur hiernaast.
    3. Zie figuur hiernaast.
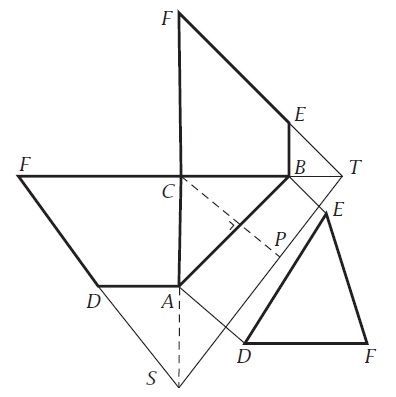
    4. Zie punt `P` in de uitslag. `CS = 8`, `CT` = 6, `ST = sqrt(8^2 + 6^2) = 10`, `CP = 6/10 * 8 = 4,8`. `PF = sqrt((4,8)^2 + 6^2 ~~ 7,68`. Dus `PF ~~ 76,8` cm en een stang van 75 cm is te kort.
    1. `G = 1,5 r^3` en `H = 6r^2` dus `H = 6 * ((G/(1,5))^(1/3))^2 ~~ 4,58 G^(2/3)`.
    2. `G = 1,5 * 4/3pi r^3` en `H = 4pi r^2` dus `H = 4pi * ((G/(2pi))^(1/3))^2 ~~ 3,69 G^(2/3)`.
    3. `G = 1,5 * pi r^3` en `H = 4pi r^2` dus `H = 4pi * ((G/(1,5pi))^(1/3))^2 ~~ 4,47 G^(2/3)`.
    4. Zie de voorgaande antwoorden. De Meeh-coëfficiënten van deze voorwerpen zijn laag, want ze hebben een vrijwel ideale vorm.
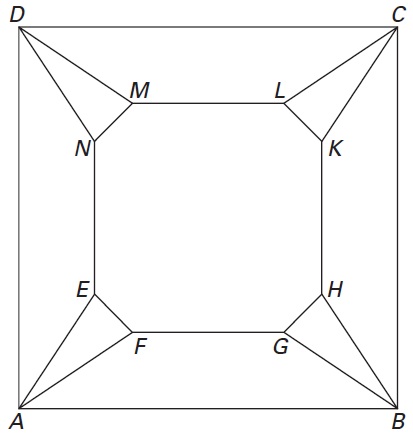
    1. De gevraagde hoek is gelijk aan `/_ABH` in de rechter figuur in de opgave. `tan(/_ABH) = 40/20 = 2` dus gevraagde hoek is ongeveer 63°.
    2. Zie de verkleinde figuur hiernaast.
    3. `GH = 10 sqrt(2)`. De omtrek van de achthoek is `4 * 10 sqrt(2) + 4 * 40 ~~ 217`. Er is ongeveer `500 – 217 = 283` cm lint over.
    4. De vier lange zijden hebben een lengte van 85 cm. De vier korte zijden hebben een lengte van `2,5 sqrt(2)` cm. De totale omtrek is (afgerond) 354 cm. Er blijft 146 cm lint over.
    5. De afstand van lijn `AB` tot lijn `FG` is `sqrt(40^2 + 20^2) = sqrt(2000)`. De oppervlakte van vierhoek `ABGF` is `70 * sqrt(2000)`. De totale oppervlakte is `4 * 70 * sqrt(2000) ~~ 12522` cm2.
    1. `sin(1/2 /_CMD) = 3/(4,8), dus `/_CMD ~~ 77`°
    2. Punt `M` tekenen uitgaande van de ligging van lijnstuk `AB`. Dan de cirkelboog `CD` tekenen en de tekening verder afmaken (hoek van 77° of spiegeling in lijn `MD` gebruiken). Zie de figuur hiernaast.
    3. `DF = sqrt(10,5^2 - 9,9^2) ~~ 3,5`. De middellijn `CD` is `2(3 + 3,5) = 13,0` cm.
    4. Op eenderde deel van de hoogte is `PQ` gelijk aan `4 1/3`. Op eenderde deel van de hoogte is `QR` gelijk aan 4. De oppervlakte is `4 1/3 * 4 + pi * (2 1/6)^2 ~~ 32` cm2.
    1. De oppervlakte van de rechthoek is `30 * 10 = 300` cm2. De oppervlakte van de twee halve cirkels is samen `pi * 5^2 ~~ 79` cm2. De oppervlakte van de vlakke zijkant is 379 cm2.
    2. De hoogte van een rechthoekige driehoek met schuine zijde 20 en basishoek 40° moet worden berekend. De hoogte is `20 * sin(40^o) ~~ 12,9. De binnenkant van het doosje moet minimaal 13 cm hoog zijn.
    3. `1/6 pi * 8^2 + 1/6 pi^2 * d * 8^2 + 1/4 pi * d^2 * 8 = 5000` geeft `2pi d^2 + 10 2/3pi d + 10 2/3pi - 5000 = 0`.
      Deze vergelijking kun je oplossen met de `abc`-formule. Dit geeft `d ~~ -34,4 vv d ~~ 21,9`.
      De totale diameter van een kaas is (ongeveer) `21,9 + 2 * 4 = 29,9` cm en `350/(29,9) ~~ 11,7` dus er passen maximaal 11 kazen naast elkaar.
    4. `d = 0` en `h = 2r` invullen in de gegevens formule geeft `V = 4/3 pi r^3`.