
Inhoud van ruimtelijke figuren
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Inhoud van ruimtelijke figuren > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Inhoud van ruimtelijke figuren > Inleiding
Bij Verkennen wordt verteld welk verband Archimedes ontdekte tussen de inhouden van een cilinder een bol en een kegel.
Probeer de formules voor de inhoud van deze lichamen te vinden, bij de Uitleg vind je het antwoord.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Inhoud van ruimtelijke figuren > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Inhoud van ruimtelijke figuren > Uitleg
Lees eerst de Uitleg goed door.
Opgaven
-
Bekijk de inhoudsformules in de Uitleg.
- Bereken de inhoud van een cilinder met een straal van 10 cm en een hoogte van 20 cm. (Reken behalve de cilindermantel ook het grondvlak een het bovenvlak mee).
- In de cilinder bij a past precies een bol. Bereken de inhoud van die bol.
-
Onze Aarde is bij ruwe benadering een bol met een omtrek van 40.000 km.
Hoe groot is de inhoud van de Aarde?
-
Hoe bepaal je de inhoud van een willekeurig niet al te groot lichaam?
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Inhoud van ruimtelijke figuren > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Inhoud van ruimtelijke figuren > Theorie
Bestudeer eerst de Theorie. In de opgaven word je naar de Voorbeelden verwezen.
Opgaven
 In de Theorie staat dat je de inhoud van lichamen die de vorm hebben van een prisma, of een cilinder kunt berekenen door de oppervlakte van het grondvlak met de hoogte te vermenigvuldigen.
Dit principe geldt heel algemeen voor lichamen waarvan elke doorsnede evenwijdig aan het grondvlak precies hetzelfde is als dat grondvlak.
In de Theorie staat dat je de inhoud van lichamen die de vorm hebben van een prisma, of een cilinder kunt berekenen door de oppervlakte van het grondvlak met de hoogte te vermenigvuldigen.
Dit principe geldt heel algemeen voor lichamen waarvan elke doorsnede evenwijdig aan het grondvlak precies hetzelfde is als dat grondvlak.
-
Bereken de inhoud van een balk met een grondvlak van 4 bij 4 cm en een hoogte van 10 cm.
-
Bereken de inhoud van een regelmatig driezijdig prisma met ribben van 6 cm.
-
Bereken de hoeveelheid plastic die nodig is voor een holle cilindervormige buis met een lengte van 1,5 m, een binnendiameter van 14 mm en een buitendiameter van 18 mm.
-
Bereken uit hoeveel cm3 hout 1 m van het profiel hiernaast bestaat. De doorsnede van het profiel heeft een oppervlakte van ongeveer 55 cm2.
Voor de inhoud van lichamen die de vorm hebben van een piramide of een kegel neem je `1/3` van de oppervlakte van het grondvlak maal de hoogte.
 Bereken de inhoud van een regelmatige vierzijdige piramide met ribben van 6 cm.
Bereken de inhoud van een regelmatige vierzijdige piramide met ribben van 6 cm.
-
Bereken de inhoud van een regelmatig viervlak met ribben van 6 cm.
-
De inhoud van dit koekje heeft een kegelvorm. De hoogte van die kegel is 10 cm, de diameter 4 cm. Hoeveel bedraagt die inhoud?
-
In Voorbeeld 1 wordt de inhoud van een afgeknotte kubus berekend.
Van kubus `ABCD.EFGH` met ribben van 10 cm wordt het deel dat hoekpunt `F` bevat afgezaagd. Het zaagvlak is vlak `EBG`.
Bereken de volume van de overblijvende afgeknotte kubus.
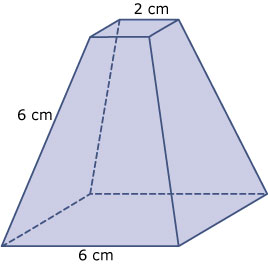 Bereken de inhoud van de afgeknotte regelmatige vierzijdige piramide hiernaast.
Zie indien nodig Voorbeeld 2.
Bereken de inhoud van de afgeknotte regelmatige vierzijdige piramide hiernaast.
Zie indien nodig Voorbeeld 2.
-
In Voorbeeld 3 wordt de inhoud van figuur berekend die is samengesteld uit een afgeknotte kegel en een halve bol.
Stel je voor dat het amsterdammertje van binnen hol is. Het metaal heeft overal een dikte van 2 mm.
Hoeveel metaal is er dan voor nodig?
Verwerken
-
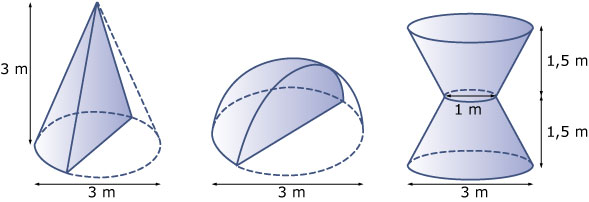
Bereken de inhoud van de volgende figuren.
-
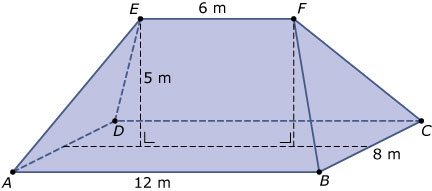
Je ziet hier een zogenaamd schilddak, een dakvorm met een rechthoekig grondvlak `ABCD` en waarbij de nok `EF` van het dak precies boven het midden van het grondvlak zit. Het dak zelf bestaat uit twee gelijkzijdige driehoeken en twee symmetrische trapezia. Bereken het volume onder dit schilddak.
-
Een piramide `T.ABCDE` heeft als grondvlak een regelmatige vijfhoek `ABCDE`. De hoogte van de piramide is `TS`, waarin punt `S` het middelpunt is van de cirkel waar de hoekpunten van het grondvlak op liggen. Alle ribben van deze piramide zijn 4 cm.
Bereken de inhoud van deze piramide.
-
Hieronder zie je het zijaanzicht van een zuiver cirkelvormige tent.
Bereken de inhoud van deze tent.

 Hier zie je een L-vormige cilindrische holle buis van staal.
Het vierkante grondplaatje van 150 mm bij 150 mm wordt aan de muur bevestigd, de buis steekt dan 450 mm naar voren en 250 mm omhoog.
De binnendiameter van de buis is 48 mm en het staal is 1 mm dik.
Hier zie je een L-vormige cilindrische holle buis van staal.
Het vierkante grondplaatje van 150 mm bij 150 mm wordt aan de muur bevestigd, de buis steekt dan 450 mm naar voren en 250 mm omhoog.
De binnendiameter van de buis is 48 mm en het staal is 1 mm dik.
Staal weegt 7,8 g/cm3.
Hoeveel zwaar is deze buis inclusief het grondplaatje?
-
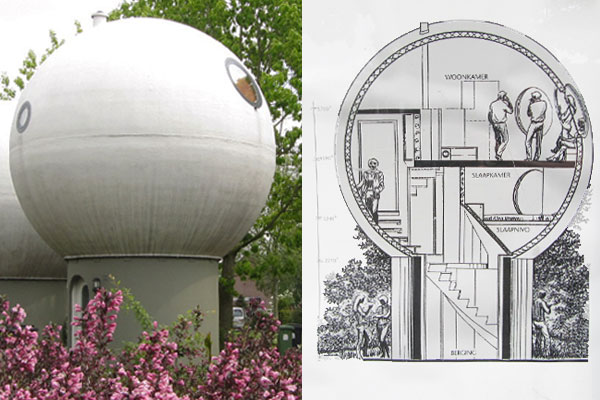
De welbekende vijftig bolwoningen met hun opvallende architectuur staan in ís-Hertogenbosch. De bolwoning is ontworpen door de beeldhouwer, ontwerper en architect Dries Kreijkamp geboren in 1937 te Tegelen. Ze zijn gebouwd in 1984, met het doel om de bewoners te laten verbinden met de natuur, mede door de diverse ronde ramen die in de woningen aanwezig zijn. Tevens zijn de woningen milieuvriendelijk, door de bolvorm heeft de wind er bijna geen greep op en daarnaast zijn ze zo ontworpen dat ze energiezuinig en goedkoop zijn. Het zijn huurwoningen voor 1 of 2 personen.
Welke oppervlakte hebben deze bolwoningen als de diameter van de bol zelf 8 meter en die van de cilinder 6 meter is, terwijl
de hoogte van de cilinder 3 meter is? Maak hierbij gebruik van de formule voor de inhoud van een bolsegment met hoogte `h` van een bol met straal `r`. De inhoud van zo'n bolsegment is `1/3pi h^2(3R - h)`.
Testen
-
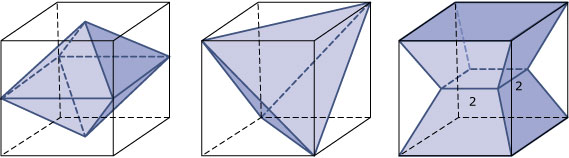
Bereken de inhoud van de volgende lichamen die precies passen in een kubus met ribben van 6 cm.
 De binnenkant van dit drinkglas heeft de vorm van een afgeknotte kegel. De diameter van de bovencirkel van deze kegel is 100 mm, die van de grondcirkel is 80 mm.
De hoogte deze afgeknotte kegel is 200 mm.
De binnenkant van dit drinkglas heeft de vorm van een afgeknotte kegel. De diameter van de bovencirkel van deze kegel is 100 mm, die van de grondcirkel is 80 mm.
De hoogte deze afgeknotte kegel is 200 mm.
Hoeveel bedraagt de inhoud van dit glas im mm3 nauwkeurig?
-
De Waura indianen wonen in het Amazonegebied in Brazilië. Hun dorpen bestaan uit een aantal grote huizen. Hieronder zie je zo'n huis. Je kunt het wiskundig beschrijven als een halve cilinder waarop aan weerszijden een kwart bol zit. Neem aan dat dit huis zo'n 6 m hoog is en dat de halve cilinder een lengte heeft van 8 m. Bereken dan de inhoud ervan.


![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Inhoud van ruimtelijke figuren > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Inhoud van ruimtelijke figuren > Inleiding![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Inhoud van ruimtelijke figuren > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Inhoud van ruimtelijke figuren > Uitleg![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Inhoud van ruimtelijke figuren > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Inhoud van ruimtelijke figuren > Theorie In de Theorie staat dat je de inhoud van lichamen die de vorm hebben van een prisma, of een cilinder kunt berekenen door de oppervlakte van het grondvlak met de hoogte te vermenigvuldigen.
Dit principe geldt heel algemeen voor lichamen waarvan elke doorsnede evenwijdig aan het grondvlak precies hetzelfde is als dat grondvlak.
In de Theorie staat dat je de inhoud van lichamen die de vorm hebben van een prisma, of een cilinder kunt berekenen door de oppervlakte van het grondvlak met de hoogte te vermenigvuldigen.
Dit principe geldt heel algemeen voor lichamen waarvan elke doorsnede evenwijdig aan het grondvlak precies hetzelfde is als dat grondvlak.
 Bereken de inhoud van een regelmatige vierzijdige piramide met ribben van 6 cm.
Bereken de inhoud van een regelmatige vierzijdige piramide met ribben van 6 cm.
 Bereken de inhoud van de afgeknotte regelmatige vierzijdige piramide hiernaast.
Zie indien nodig Voorbeeld 2.
Bereken de inhoud van de afgeknotte regelmatige vierzijdige piramide hiernaast.
Zie indien nodig Voorbeeld 2.


 Hier zie je een L-vormige cilindrische holle buis van staal.
Het vierkante grondplaatje van 150 mm bij 150 mm wordt aan de muur bevestigd, de buis steekt dan 450 mm naar voren en 250 mm omhoog.
De binnendiameter van de buis is 48 mm en het staal is 1 mm dik.
Hier zie je een L-vormige cilindrische holle buis van staal.
Het vierkante grondplaatje van 150 mm bij 150 mm wordt aan de muur bevestigd, de buis steekt dan 450 mm naar voren en 250 mm omhoog.
De binnendiameter van de buis is 48 mm en het staal is 1 mm dik.

 De binnenkant van dit drinkglas heeft de vorm van een afgeknotte kegel. De diameter van de bovencirkel van deze kegel is 100 mm, die van de grondcirkel is 80 mm.
De hoogte deze afgeknotte kegel is 200 mm.
De binnenkant van dit drinkglas heeft de vorm van een afgeknotte kegel. De diameter van de bovencirkel van deze kegel is 100 mm, die van de grondcirkel is 80 mm.
De hoogte deze afgeknotte kegel is 200 mm. 