Inhoud van ruimtelijke figuren

Antwoorden bij de opgaven

1. 1. inh(cilinder) `= pi * 10^2 * 20 = 200pi`
   2. opp(bol) `= 4/3 pi * 10^3 = (4000pi)/3`
2. De straal van de Aarde is `40000/(2pi) ~~ 6366` km.
   De inhoud is daarom ongeveer `6366,...^3 * 4/3 pi ~~ 1,081 * 10^(12)` km².
3. Je dompelt het onder in een rechthoekige (balkvormige) bak water en meet dat de vorm (dus lengte, breedte en hoogte) van de extra hoeveelheid water.
   Zo maak je van een willekeurige vorm een balkvorm met dezelfde inhoud.
4. 1. inhoud `= 4 * 4 * 10 = 160` cm³
   2. inhoud `= 1/2 * 6 * sqrt(6^2 - 3^2) * 6 = 18 sqrt(27)` cm³
   3. inhoud `= pi * 0,9^2 * 150 - pi * 0,7^2 * 150 = 48pi` cm³
   4. inhoud `= 55 * 100 = 5500` cm³
   5. inhoud `= 1/3 * 6 * 6 * sqrt(18) = 12 sqrt(18)` cm³
   6. inhoud `= 1/3 * 1/2 * 6 * sqrt(27) * sqrt(24) = sqrt(648) = 18 sqrt(2)` cm³
   7. inhoud `= 1/3 * pi * 2^2 * 10 = 40/3 pi` cm³
5. De gevraagde inhoud is `10 * 10 * 10 - 1/3 * 1/2 * 10 * 10 * 10 = 833 1/3` cm³.
6. In het voorvlak bereken je de opstaande ribben van de ontbrekende punt via `r/(r+6) = 2/6` en dus `r = 3`.
   De hoogte van de complete piramide is dan `sqrt(9^2 - (sqrt(18))^2) = sqrt(63)`.
   De hoogte van de ontbrekende bovenste punt is `sqrt(3^2 - (sqrt(2))^2) = sqrt(7)`
   De gevraagde inhoud is `1/3 * 6 * 6 * sqrt(62) - 1/3 * 2 * 2 * sqrt(7) ~~ 93,36` cm³.
7. De inhoud van het massieve lichaam is in Voorbeeld 3 berekend. Op dezelfde manier bereken je de inhoud van de binnenruimte als het lichaam niet massief is:
   `1/3pi * 9,8^2 * 225 - 1/3 * 5,8^2 * 135 + 0,5 * 4/3pi * 5,8^2`.
   Het holle amsterdammertje heeft nu een volume van ongeveer `18925 - 17944 = 981` cm³.
8. inhoud(halve kegel) `= 1/3 * 1/2 pi * 1,5^2 * 3 = 1,125pi`
   inhoud(kwart bol) `= 1/4 * 4/3pi * 1,5^3 = 1,125pi`
   inhoud(diabolo) `= 2 * (1/3pi * 1,5^2 * 2,25 - 1/3pi * 0,5^2 * 0,75) = 3,25pi`
9. Het volume onder dit schilddak hoort bij een lichaam dat bestaat uit een driehoekig prisma (op z'n kant) met aan weerszijden twee gelijke halve piramides (die je kunt samenvoegen tot één piramide). De inhoud wordt daarom: `1/2 * 8 * 5 * 6 + 1/3 * 8 * 6 * 5 = 160` m³.
10. Het grondvlak bestaat uit vijf gelijkbenige driehoeken met een tophoek van 72°, een basis van 4 cm, twee benen van `2/(sin(36^o))` en een hoogte van `2/(tan(36^o))`. De oppervlakte van die vijfhoek is daarom `5 * 1/2 * 4 * 2/(tan(36^o)) ~~ 27,53` cm².
    De hoogte van deze regelmatige vijfzijdige piramide is `sqrt(4^2 - (2/(sin(36^o)))^2) ~~ 2,10` cm.
    De inhoud is daarom ongeveer `1/3 * 27,53 * 2,10 ~~ 19,3` cm³.
11. `1/3 pi * 2^2 * 12 - 1/3 pi * 1,5^2 * 9 + 1/3 pi * 1,5^2 * 1 = 10pi`
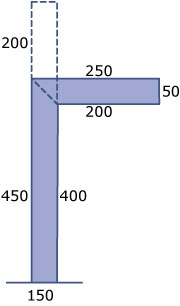12. Zaag de buis (in gedachten) in de haakse bocht over de lasnaad door en maak hem recht, zie zijaanzicht hiernaast. De hoeveelheid staal wordt (aangenomen dat er in de grondplaat geen gat zit): `150 * 150 * 1 + pi * 25^2 * 650 - pi * 24^2 * 650 ~~ 122560` mm³.
    Dat is 122,56 cm³. Dus het geheel weegt 956 gram.
13. inhoud `= 4/3pi * 4^3 - 1/3pi (4 - sqrt(4^2 - 3^2))^2 * (3*4 - (4 - sqrt(4^2 - 3^2))) + pi * 3^2 * 3 ~~ 337,8` m³
14. inhoud(linker figuur) `= 2 * 1/3 * 6 * 6 * 3 = 72` cm³
    inhoud(middelste figuur) `= 6 * 6 * 6 - 4 * 1/3 * 1/2 * 6 * 6 * 6 = 72` cm³
    inhoud(rechter figuur) `= 2 * (1/3 * 6 * 6 * 4,5 - 1/3 * 2 * 2 * 1,5) = 104` cm³
15. De inhoud is `1/3 pi * 50^2 * 1000 - 1/3 pi * 40^2 * 800 ~~ 1277581` mm³ en dat is ongeveer 1,278 liter.
16. `1/2 * 4/3pi * 6^3 + 1/2pi * 6^2 * 8 = 288pi ~~ 905` m³.