Oppervlakte van vlakke figuren

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Oppervlakte van vlakke figuren > Inleiding

Probeer bij Verkennen de oppervlakteformules van de meest gangbare vlakke figuren af te leiden uit die van de rechthoek. Het is niet erg als ze niet allemaal lukken, verder op wordt hierop terug gekomen.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Oppervlakte van vlakke figuren > Uitleg

Lees eerst de Uitleg goed door.

Opgaven

1. Bekijk de applet in de Uitleg.
   1. Beweeg punt `C` tot punt `D` tussen `A` en `B` ligt en `AD = 1`. Laat zien dat de oppervlakte van `Delta ABC` inderdaad 10 is door hem in twee halve rechthoeken te verdelen.
   2. Doe hetzelfde als `AD = 2`.
   3. Teken zelf zo'n scherphoekige driehoek `ABC`. Neem aan dat `AD = p`, `BD = q`, `AB = b` en `CD = h`. Toon aan dat opp`(Delta ABC) = 1/2 * b * h`.
   4. Beweeg punt `C` tot punt `D` links van `A` ligt en `AD = 1`. Laat zien dat de oppervlakte van `Delta ABC` inderdaad 10 is door van halve rechthoeken gebruik te maken.
   5. Teken zelf zo'n stomphoekige driehoek `ABC` met `D` links van `A`. Neem aan dat `AD = p`, `AB = b` en `CD = h`. Toon aan dat opp`(Delta ABC) = 1/2 * b * h`.


2. Bekijk de Uitleg, pagina 2.
   Leg uit hoe daarin de formule voor de oppervlakte van de cirkel wordt afgeleid uit die voor de omtrek.
   Welke aannames worden er gedaan?
   

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Oppervlakte en inhoud > Oppervlakte van vlakke figuren > Theorie

Bestudeer eerst de oppervlakteformules in de Theorie. In de opgaven word je naar de Voorbeelden verwezen.

Opgaven

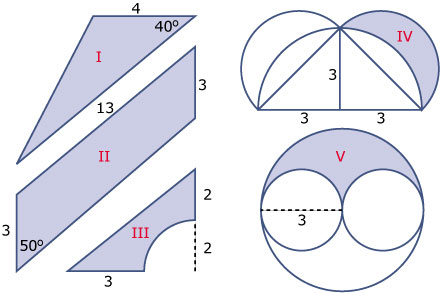
3. In de Theorie zie je de oppervlakteformules van een rechthoek, een parallellogram, een driehoek en een cirkel. Gebruik deze formules om van deze vijf gekleurde gebieden de oppervlakte te berekenen. Ga er van uit dat alle cirkelbogen precies hele, halve of kwart cirkels zijn en dat figuur II een parallellogram is.
   
   
   
   


4. Bekijk Voorbeeld 1. In dat voorbeeld wordt het berekenen van de oppervlakte van een trapezium besproken.
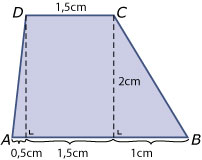
   1. Bekijk het trapezium hiernaast. Bereken er de oppervlakte van door het te verdelen in een rechthoek en twee halve rechthoeken.
   2. Bereken de oppervlakte nog eens door het trapezium met behulp van een diagonaal in twee driehoeken te verdelen.
   3. Bereken de oppervlakte tenslotte met behulp van de oppervlakteformule die in Voorbeeld 2 wordt afgeleid.


5. In Voorbeeld 2 wordt de oppervlakte van een regelmatige tienhoek berekend.
   1. Bereken de oppervlakte van een regelmatige zeshoek met zijden van 5 cm.
   2. Bereken de oppervlakte van een regelmatige vijfhoek met zijden van 5 cm.
   3. Bereken de oppervlakte van een regelmatige twintighoek die precies past binnen een cirkel met een diameter van 10 cm.
   4. Hoeveel bedraagt de oppervlakte van het gebied binnen de cirkel, maar buiten de regelmatige twintighoek bedoeld bij b?


6. In Voorbeeld 3 zie je hoe je de oppervlakte van een cirkelsector berekent.
   1. In de applet staat ingesteld een middelpuntshoek (ook wel sectorhoek genoemd) van 60° en een straal van 2.
      Leg uit waarom de oppervlakte van deze sector `1/6` deel is van die van de cirkel. Bereken met behulp daarvan de oppervlakte in twee decimalen nauwkeurig en controleer je antwoord met de applet.
   2. Bereken nu de oppervlakte van een sector met een middelpuntshoek van 75° en een straal van 1,5. Controleer je antwoord met de applet.
   3. Oefen het berekenen van de oppervlakte van een cirkelsector met behulp van de applet.


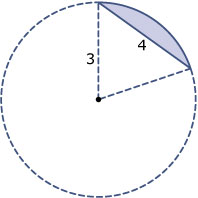7. Bereken de oppervlakte van het cirkelsegment dat hiernaast is ingekleurd.
   


8. Van elke vlieger `ABCD` staan de diagonalen `AC` en `BD` loodrecht op elkaar. Neem verder aan dat `AB = AD`.
   1. Neem aan dat `AC = 6` en `BD = 4`. Hoe groot is dan de oppervlakte van `ABCD`?
   2. Waarom maakt het voor de oppervlakte van deze vlieger niet uit waar het snijpunt van beide diagonalen precies zit? En klopt dat ook als het snijpunt van beide diagonalen niet op lijnstuk `AC` ligt, maar op het verlengte ervan? (Je hebt dan een pijlpuntvlieger.)
   3. Welke formule kun je opstellen voor de oppervlakte van een vlieger?

Verwerken

9. Bereken de oppervlakte van de volgende figuren. Figuur II is een trapezium en figuur III een vlieger. De cirkelbogen die de figuren IV en V begrenzen zijn halve dan wel kwart cirkels.
   
   
   
   


10. Van de regelmatige achthoek hiernaast liggen alle hoekpunten op een cirkel met een straal van 5 cm.
    Bereken de oppervlakte van het gebied dat buiten de achthoek en binnen de cirkel ligt.
    


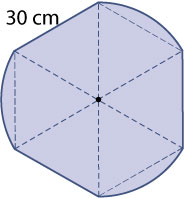
11. Iemand maakt een driepotig krukje waarvan de zitting van boven gezien deze vorm heeft. De figuur bestaat uit een regelmatige zeshoek waaraan op drie zijden een segment zit van de cirkel door de hoekpunten van de zeshoek.
    Bereken zowel de oppervlakte als de omtrek van deze zitting.
    
    
    
    


12. Deze symmetrische bak staat precies half vol met water. De bak is 2 meter lang. De voorkant en de achterkant staan loodrecht op de bodem van de bak.
    
    
    
    
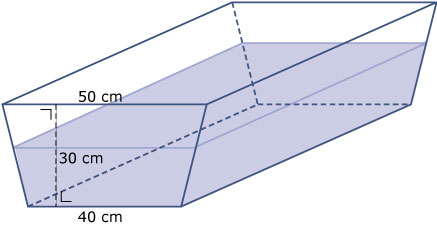
    1. Hoe hoog staat de waterspiegel gerekend vanaf de bodem van de bak?
    2. Hoe groot is de oppervlakte van de waterspiegel?

Testen

13. Bereken de oppervlakte van de volgende figuren. Figuur II is een vlieger en figuur III een trapezium. Figuur IV bestaat uit vijf gelijke cirkels in één grote cirkel.
    
    
    
    


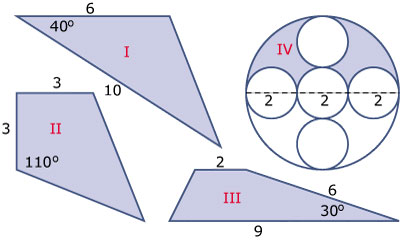
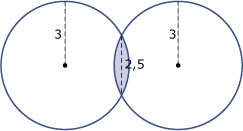
14. Bereken de oppervlakte van het gebied binnen beide cirkels.