Totaalbeeld

Antwoorden bij de opgaven

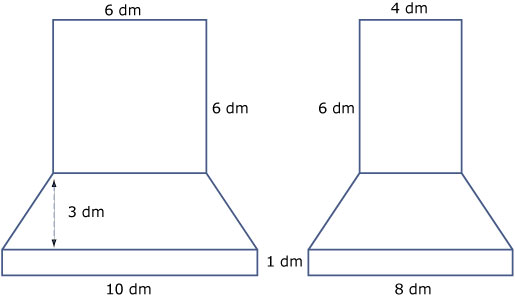
1. 1. Hier zie je vooraanzicht en zijaanzicht. Het bovenaanzicht staat bij c.
      
      
   2. De hoogte van zo'n trapezium is `sqrt(3^2 + 2^2) = sqrt(13)`.
      De zijden zijn `10`, `6` en `sqrt(17)` dm.
      De hoeken zijn `61^o` en `119^o`.
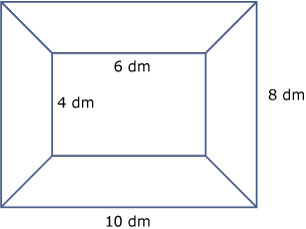
   3. In het bovenaanzicht zie je meteen dat de vier schuine opstaande ribben van het middelste deel niet in één punt samenkomen.
      
      
   4. Er zijn veel goede uitslagen mogelijk. Let vooral op de correcte afmetingen van de trapezia.
      Bij twijfel laten controleren!
2. De afgesneden kegel heeft een hoogte `h` waarvoor geldt: `(64)/(46) h = h + 90`, zodat `h = 230` mm.
   De uitslag van dit koffiebekertje is daarom een sector uit een cirkel met een straal van `sqrt(310^2 + 32^2)` min een sector uit een cirkel met een straal van `sqrt(230^2 + 23^2)` met hetzelfde middelpunt. De sectorhoek is `32/sqrt(310^2 + 32^2) * 360^o ~~ 37^o`. En natuurlijk moet je de bodem (een cirkel met een straal van 23 mm) niet vergeten.
3. 1. 
   2. De zijden hebben een lengte van `sqrt(3^2 + 3^2) = sqrt(18)`, net als de kortste diagonaal.
      Elke ruit bestaat dus uit twee gelijkzijdige driehoeken.
      De hoeken zijn daarom `60^o` en `120^o`.
   3. Zie de figuur hiernaast.
4. 1. 
      
      
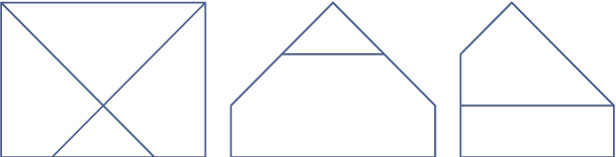
   2. `FGTK` is een vierhoek met `/_GFK = 90^o`, `FG = 6`, `FK = sqrt(8)`, `FK = sqrt(12)` en `GT = sqrt(48)` m.
      `/_FGT ~~ 55^o`, `/_FKT ~~ 145^o` en `/_KTG ~~ 70^o`.
   3. Omdat voorvlak en achtervlak van de schuur evenwijdig zijn, ligt ook `CD` in vlak `CLK`.
      Teken het snijpunt `P` van `LK` en `BF` en trek `PC`. Deze lijn snijdt `FG` in `Q`.
      Teken het snijpunt `R` van `KL` en `AE` en trek `RD`. Deze lijn snijdt `EH` in `S`.
      `KQCDSL` is de gevraagde doorsnede.
5. 1. Omdat `AS = BS = CS = DS = ES = FS = 4` cm, moet `AT > 4` cm om een piramide te krijgen.
   2. `AT = sqrt(6^2 + 4^2) = sqrt(52)` cm.
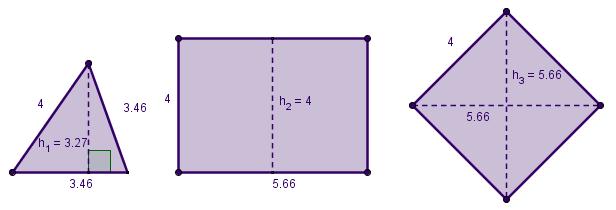
   3. De doorsnede door `M` wordt een gelijkbenige driehoek met een basis van `4 sqrt(3)` en een hoogte van 3 cm. De doorsnede door `N` is eenzelfde driehoek.
      De doorsnede door `S` wordt een gelijkbenige driehoek met een basis van `4 sqrt(3)` en hoogte `ST = 6` cm.
6. Dit is een echt pittige opgave, beschouw hem als een uitdaging!
   1. 
   2. Tetraëder: `h = 1/3 r sqrt(6)`.
      Kubus: `h = r`.
      Octaëder: `h = r sqrt(2)`.
   3. Alle grensvlakken zijn regelmatige veelhoeken. De hoeken daarvan zijn `60^o` (bij driehoeken), `90^o` (bij vierhoeken), `108^o` (bij vijhoeken), `120^o` (bij zeshoeken), etc. De hoeken om elk hoekpunt van de figuur moeten samen kleiner zijn dan `360^o`, anders krijg je geen ruimtelijke figuur. Verder komen er in zo'n hoekpunt altijd 3 of meer vlakken bij elkaar. Het aantal mogelijkheden is dus beperkt:
      • Komen er drie (gelijkzijdige) driehoeken in elk hoekpunt bij elkaar, krijg je een tetraëder (regelmatig viervlak).
      • Komen er vier (gelijkzijdige) driehoeken in elk hoekpunt bij elkaar, krijg je een octaëder (regelmatig achtvlak).
      • Komen er vijf (gelijkzijdige) driehoeken in elk hoekpunt bij elkaar, krijg je een icosaëder (regelmatig twintigvlak).
      • Komen er drie vierkanten in elk hoekpunt bij elkaar, krijg je een kubus.
      • Komen er drie regelmatige vijfhoeken in elk hoekpunt bij elkaar, krijg je een dodecaëder (regelmatig twaalfvlak).
      Alle andere mogelijkheden leveren `360^o` of meer op voor de hoeken rond elk hoekpunt...
   4. Zie www.ics.uci.edu/~eppstein/junkyard/euler/ voor 19 bewijzen van de formule van Euler (Engelstalig).
7. 1. Het bovenaanzicht wordt een vierkant met zijden van 40 mm en de twee diagonalen er in.
      Bij elk hoekpunt en het snijpunt van de diagonalen komen twee letters: `P` en `Q` bij het snijpunt van de diagonalen en verder bij elk hoekpunt de letters van de punten die recht boven elkaar liggen.
   2. `P` ligt `46 – 13 = 33` cm boven het midden van het grondvlak. De lengte van `AP` is `sqrt(20^2 + 20^2 + 33^2)`. De lengte van `AF` is `sqrt(40^2+ 46^2)`. De gevraagde lengte is `8 * sqrt(1889) + 8 * sqrt(3716) ~~ 835` cm.
   3. De lengte van `PQ` is `46 – 2 * 13 = 20`.
      `QS : SG = PQ : CG = 20 : 46` (of `QS : SG = QM : MN = 10 : 23`, waarbij `M` en `N` de middens zijn van respectievelijk `PQ` en `EG`). `QS = 20/66 * sqrt(1889)` geeft 132 mm (of 13,2 cm).
8. 1. De oppervlakte van de hele kubus is `6 * 100^2 = 60000` cm². De oppervlakte van (bijvoorbeeld) `Delta HPQ` is `1/2 * 20^2 = 200` cm². De gevraagde oppervlakte is `60000 – 3 * 200 = 59400` cm².
   2. 
   3. `BH = 100 sqrt(3)` en de hoogte van viervlak `H.PQR` is `HZ` (met `Z` zwaartepunt van driehoek `PQR`). De zwaartelijnen van `Delta PQR` zijn `10 sqrt(6)` en `PZ = 20/3 sqrt(6)`. `HZ^2 = 20^2 – (20/3 * sqrt(6))^2`, dus `HZ = 20/3 * sqrt(3)`. De hoogte van `B` boven de sokkel is `100 sqrt(3) – 20/3 sqrt(3) ~~ 161,66`.
      `161,66 + 20` is minder dan 185 (cm).
9. 
   1. Je krijgt drie gelijkbenige rechthoekige driehoeken met rechthoekszijden van 5 cm.
   2. De afstand van `K` tot de muur is gelijk aan `3 * AL`. `AL = 12,5 sqrt(2) ~~ 17,68`. De gevraagde afstand is 53 cm.
   3. De grijze (rechthoekige) driehoeken hebben een hoek van `60^o` bij de hoekpunten `S`, `T` en `U`. De rechthoekszijde van een gearceerde driehoek die bij een hoekpunt ligt, is `25/(tan(60^o))`. De schuine zijde van een gearceerde driehoek is `25/(sin(60^o))`.
      `ST = 25 + 25/(sin(60^o)) + 25/(tan(60^o)) ~~ 68` cm.