Series evenwijdige doorsneden

Antwoorden bij de opgaven

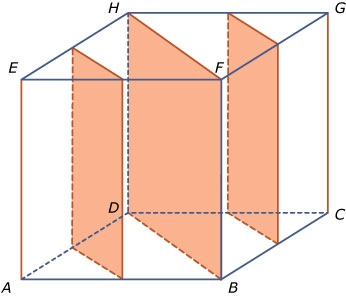
1. De doorsneden evenwijdig aan `ABCD` zijn allemaal precies dezelfde vierkanten van 4 cm bij 4 cm.
   Zie verder de figuur hiernaast.
2. Zie de figuur hieronder.
   
   
3. Controleer je antwoorden door in voorbeeld 1 in de applet punt `S` te bewegen.
4. 1. 
   2. 
5. Volg de constructie in voorbeeld 3 stap voor stap.
   4. Begin met een lijn door `E` en evenwijdig `PQ`. Deze lijn snijdt `AB` in `K`.
      Trek een lijn door `K` en evenwijdig `PD`. Deze lijn snijdt `AD` in `L`.
      `Delta EKL` is de gevraagde doorsnede.
6. 1. 
   2. 
7. 1. 
   2. Zie figuur.
   3. Dat is alleen punt `E`.
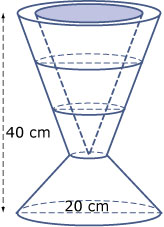
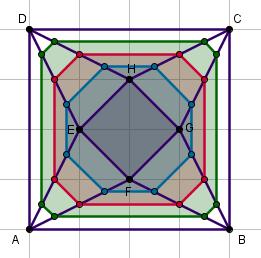8. Dit gaat het gemakkelijkst in een bovenaanzicht van de achtkanter.
   Zie hiernaast.
9. Het zijn doorsneden van een kegel met een straal van 3 cm en een hoogte van 3 cm.
10. 
11. In een bovenaanzicht kun je de breedte van elke doorsnede opmeten of berekenen.
    De eerste doorsnede is een punt.
    De tweede doorsnede heeft een breedte van `sqrt(3^2 - 2^2) = sqrt(5)` cm en een hoogte van `1/3 * 5 = 1 2/3` cm en heeft een paraboolvorm.
    De derde doorsnede heeft een breedte van `sqrt(3^2 - 1^2) = sqrt(8)` cm en een hoogte van `2/3 * 5 = 3 1/3` cm en heeft ook een paraboolvorm.
    De vierde doorsnede is een gelijkbenige driehoek met een basis van 6 cm en een hoogte van 5 cm.
    De vijfde doorsnede is gelijk aan de derde, de zesde doorsnede is gelijk aan de tweede en de zevende doorsnede is weer een punt.
12. In een aanzicht kun je de breedte van elke doorsnede opmeten of berekenen.
    De eerste doorsnede is een punt.
    De tweede doorsnede is een cirkel met een straal van `sqrt(3^2 - 2^2) = sqrt(5)` cm.
    De tweede doorsnede is een cirkel met een straal van `sqrt(3^2 - 1^2) = sqrt(8)` cm.
    De vierde doorsnede is een cirkel met een straal van 3 cm.
    De vijfde doorsnede is gelijk aan de derde, de zesde doorsnede is gelijk aan de tweede en de zevende doorsnede is weer een punt.
13. 
14.