
Doorsneden
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Doorsneden > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Doorsneden > Inleiding
Probeer de opdrachten bij Verkennen zo goed mogelijk uit te voeren.
Met de rechter muisknop kun je de figuur bewegen en hem zo van alle kanten bekijken.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Doorsneden > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Doorsneden > Uitleg
Lees eerst de Uitleg goed door. Je vindt daar ook enkele antwoorden op de opdrachten die je bij Verkennen moest uitvoeren.
Opgaven
-
Bekijk de Uitleg.
- Waarom zijn de twee ribben `AP` en `QG` evenwijdig?
- Teken diagonaalvlak `ACGE` op ware grootte en laat zien dat `AG` en `EM` loodrecht op elkaar staan als `M` het midden van `AC` is.
- Waarom zie je `APGQ` op ware grootte als je in de richting `EM` op dat vlak kijkt?
- Bereken zelf de twee diagonalen van ruit `APGQ`.
- Teken de ruit op ware grootte en bereken de hoeken ervan.
-
Bekijk de kubus van de Uitleg. Teken zelf die kubus. Door `A`, `P` en `H` gaat een vlak.
Dat vlak kun je binnen de kubus nog groter maken.
- Leg uit waarom het midden `R` van `FG` ook in dit vlak ligt. (Denk aan evenwijdigheid!)
- Teken vierhoek `APRH` in de kubus.
- Leg uit dat alle punten van het vlak door `A`, `P` en `H` die binnen de kubus liggen binnen of op vierhoek `APRH` liggen.
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Doorsneden > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Doorsneden > Theorie
Bestudeer eerst de Theorie. In de opgaven word je naar de Voorbeelden verwezen.
Vooral het begrip doorsnede van een vlak met een ruimtelijke figuur is van belang.
Je leert ook zelf doorsneden tekenen.
Opgaven
-
In Voorbeeld 1 zie je hoe je een gegeven doorsnede op ware grootte kunt tekenen.
- Laat zien hoe de zijden van vierhoek `AFPQ` kunnen worden berekend.
- Bereken zelf de diagonalen van vierhoek `AFPQ`.
- Waarom weet je zeker dat vierhoek `AFPQ` een trapezium is?
- Teken nu dit trapezium op ware grootte.
-
In Voorbeeld 2 wordt de doorsnede `PQRT` op ware grootte getekend.
-
Teken zelf deze doorsnede op ware grootte. Controleer alle berekende lengtes.
-
Bereken de hoeken en de oppervlakte van het trapezium.
-
Hoe je zelf een doorsnede tekent zie je in Voorbeeld 3. Daar wordt de doorsnede van het vlak door `P`, `Q` en `R` en een gegeven kubus geconstrueerd.
-
Teken zo'n kubus. Voer daarna zelf de constructie stap voor stap uit.
Leg bij elke stap uit hoe en waarom hij wordt gezet.
-
Op Voorbeeld 3, pagina 2 zie je de berekening van de oppervlakte van de doorsnede.
Voer die berekening zelf uit.
-
Teken de kubus nog eens. Het midden van `GH` is punt `S`, het midden van `BF` is punt `Q`.
Teken de doorsnede van het vlak door `E`, `Q` en `S` met de kubus.
Geef ook nu een uitgebreide beschrijving van je constructie.
-
In Voorbeeld 4 wordt de doorsnede van het vlak door `P`, `Q` en `R` en een gegeven regelmatige vierzijdige piramide geconstrueerd.
-
Waarom weet je zeker dat de lijnen `RQ` en `AC` elkaar snijden?
Waarom ligt dit snijpunt `K` in het grondvlak `ABCD` van de piramide?
-
Geef een nauwkeurige beschrijving van de constructie.
-
Teken zelf deze piramide en daarin de doorsnede van het vlak door `R`, `B` en `Q`.
 Het ontwerp van de kubuswoning door architect Piet Blom is beroemd. In Helmond en in Rotterdam zijn van deze kubuswoningen gebouwd.
Het ontwerp van de kubuswoning door architect Piet Blom is beroemd. In Helmond en in Rotterdam zijn van deze kubuswoningen gebouwd.

-
Teken zo'n kubus die op zijn punt staat: één van de lichaamsdiagonalen is verticaal.
-
Teken de vloeren van de drie verdiepingen in de kubus.
Deze drie vloeren verdelen de verticale lichaamsdiagonaal in vier gelijke delen.
Verwerken
-
Je ziet hier een prisma `ABC.DEF` waarvan twee grensvlakken vierkant zijn. Deze vierkanten hebben zijden van 4 cm.
Verder is gegeven: `/_BAC = 90^o`, `BG = 1` en `CH = 1`.

- Teken de doorsnede van vlak `GHD` en het prisma op ware grootte.
- Bereken de grootte van de hoeken van driehoek `GHD`.
- Teken in de figuur de snijlijn van vlak `GHD` met grondvlak `ABC`.
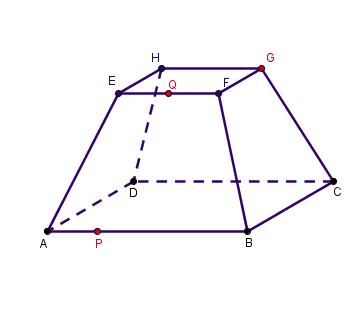
 Van de achtkanter `ABCD.EFGH` is het grondvlak `ABCD` een vierkant van 4 bij 4, de hoogte 4 en het bovenvlak `DEFG` een vierkant met diagonalen van 2 eenheden. In deze achtkanter is een horizontale doorsnede getekend door de midden van alle opstaande ribben.
Van de achtkanter `ABCD.EFGH` is het grondvlak `ABCD` een vierkant van 4 bij 4, de hoogte 4 en het bovenvlak `DEFG` een vierkant met diagonalen van 2 eenheden. In deze achtkanter is een horizontale doorsnede getekend door de midden van alle opstaande ribben.
-
Teken deze doorsnede op ware grootte. Laat zien hoe je daarbij te werk gaat.
-
Bereken de totale omtrek van deze doorsnede.
-
Teken de doorsnede van het vlak door `P`, `Q` en `C` en de regelmatige vierzijdige piramide `T.ABCD`.
Geef een beschrijving van de constructie.

-
Teken de doorsnede van het vlak door `P`, `Q` en `R` en het regelmatige driezijdige prisma `ABC.DEF`.
Geef een beschrijving van de constructie.

-
In deze balk `ABCD.EFGH` is `P` het midden van `EF` en ligt `Q` op `CG` zo, dat `CQ : QC = 2 : 1`.
Teken de doorsnede van het vlak `APQ` en de balk.
Geef een beschrijving van de constructie.

Testen
 Van een regelmatige vierzijdige piramide `T.ABCD` is het grondvlak `ABCD` een vierkant met zijden van 4 cm. De hoogte van deze piramide is 5 cm. Punt `E` is het midden van `BT` en punt `G` is het midden van `DT`. De doorsnede `AEFG` heeft de vorm van een vlieger.
Van een regelmatige vierzijdige piramide `T.ABCD` is het grondvlak `ABCD` een vierkant met zijden van 4 cm. De hoogte van deze piramide is 5 cm. Punt `E` is het midden van `BT` en punt `G` is het midden van `DT`. De doorsnede `AEFG` heeft de vorm van een vlieger.
-
Leg uit waarom deze doorsnede de vorm van een vlieger heeft.
-
Teken doorsnede `AEFG` op ware grootte. Licht je antwoord met berekeningen toe.
-
Bereken de grootte van `/_EAG`.
-
Dit is een afgeknotte regelmatige vierzijdige piramide `ABCD.EFGH`.
`P` ligt zo op `AB` dat `AP : PB = 1 : 3` en `Q` is het midden van `EF`.
Teken de doorsnede van het vlak `PQG` en de afgeknotte piramide.
Geef een beschrijving van de constructie.

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Doorsneden > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Doorsneden > Inleiding![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Doorsneden > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Doorsneden > Uitleg![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Doorsneden > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Doorsneden > Theorie Het ontwerp van de kubuswoning door architect Piet Blom is beroemd. In Helmond en in Rotterdam zijn van deze kubuswoningen gebouwd.
Het ontwerp van de kubuswoning door architect Piet Blom is beroemd. In Helmond en in Rotterdam zijn van deze kubuswoningen gebouwd.

 Van de achtkanter `ABCD.EFGH` is het grondvlak `ABCD` een vierkant van 4 bij 4, de hoogte 4 en het bovenvlak `DEFG` een vierkant met diagonalen van 2 eenheden. In deze achtkanter is een horizontale doorsnede getekend door de midden van alle opstaande ribben.
Van de achtkanter `ABCD.EFGH` is het grondvlak `ABCD` een vierkant van 4 bij 4, de hoogte 4 en het bovenvlak `DEFG` een vierkant met diagonalen van 2 eenheden. In deze achtkanter is een horizontale doorsnede getekend door de midden van alle opstaande ribben.



 Van een regelmatige vierzijdige piramide `T.ABCD` is het grondvlak `ABCD` een vierkant met zijden van 4 cm. De hoogte van deze piramide is 5 cm. Punt `E` is het midden van `BT` en punt `G` is het midden van `DT`. De doorsnede `AEFG` heeft de vorm van een vlieger.
Van een regelmatige vierzijdige piramide `T.ABCD` is het grondvlak `ABCD` een vierkant met zijden van 4 cm. De hoogte van deze piramide is 5 cm. Punt `E` is het midden van `BT` en punt `G` is het midden van `DT`. De doorsnede `AEFG` heeft de vorm van een vlieger.
