Aanzichten en uitslagen

Antwoorden bij de opgaven

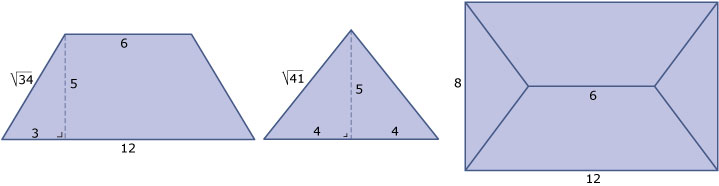
1. 1. Het bovenaanzicht.
   2. Werk in symmetrisch trapezium `ACGE`. De hoogte is `sqrt(6^2 - (1,5sqrt(2))^2) = sqrt(31,5)`.
   3. Voor- en zijaanzicht krijgen nu een hoogte van ongeveer 5,6.
2. 1. Die hoogte wordt nu `sqrt(6^2 - 1,5^2) = sqrt(33,75)`.
   2. Alleen de hoogtes van de vier opstaande zijvlakken worden nu anders, namelijk ongeveer 5,8.
3. 1. Bij twijfel laten controleren.
   2. Bij twijfel laten controleren.
4. 
   1. Eerst de hoogte berekenen in een diagonaalvlak: `h = sqrt(18) ~~ 4,2`.
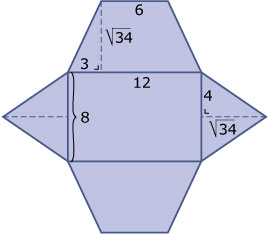
   2. Eerst de hoogte van een zijvlak berekenen: `h_(text(zijvlak)) = sqrt(6^2 - 3^2) = sqrt(27) ~~ 5,2`. Hiernaast zie je de uitslag.
5. Voor de uitslag van de linker figuur bereken je eerst de hoogte van een opstaand zijvlak: `sqrt(6^2 - 1,5^2) = sqrt(33,75)`. Voor de aanzichten bereken je de hoogte van de afgeknotte piramide zelf: `sqrt(6^2 - (1,5sqrt(2))^2) = sqrt(31,5)`. De uitslag wordt:
   
   
   
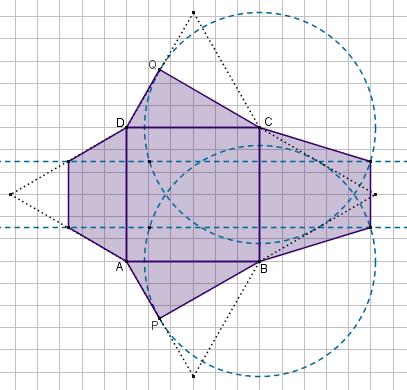
   Voor de uitslag van de rechterfiguur bereken je de zijden van `Delta PQR`. Deze zijn allemaal `sqrt(8)`. Hier zie je de uitslag en de drie aanzichten:
   
       
6. Het wordt een piramide `T.ABCD` met grondvlak `ABCD` een rechthoek van 4 bij 3.
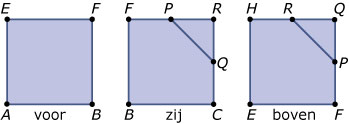
   De top `T` zit recht boven punt `C` met `CT = 3`.
7. 
   1. Je berekent de omtrek van de grondcirkel van de kegel en de omtrek van de cirkel waar de kegelmantel een deel van is. De grootte van dat deel wordt bepaald door de sectorhoek. Deel je de omtrek van de grondcirkel door de omtrek van de cirkel waar de kegelmantel een deel van is, dan weet je welk deel van de `360^o` de sectorhoek is. Je vindt ongeveer `113^o`.
      Voor de uitslag teken je nu de cirkel met straal `AT = sqrt(40)`.
      Daarbinnen meet je een sector met (met het middelpunt als hoekpunt) een hoek van `113^o` af.
      De grondcirkel van de kegel voeg je nog toe.
   2. Zie hiernaast.
   3. 
      
8. 1. Uit 6 gelijkbenige driehoeken met hoeken van `(360/6)^o = 60^o`.
      Deze zeshoek bestaat daarom uit 6 gelijkzijdige driehoeken met zijden van 4 cm.
   2. Maak een cirkel met straal 4 cm. Zet in het middelpunt naast elkaar 6 hoeken van `60^o` uit. De benen van die hoeken snijden de cirkel in 6 punten. Als je steeds twee opvolgende punten met elkaar verbindt, krijg je de regelmatige zeshoek.
   3. 
      
   4. Van het grondvlak zijn alle ribben 4 eenheden, het gaat dus om de opstaande ribben.
      Ribbe `DT = 6` en ribben `CT = ET = sqrt(4^2 + 6^2) = sqrt(52)`.
      Ribben `BT = FT = sqrt((4sqrt(3))^2 + 6^2) = sqrt(84)`.
      Ribbe `AT = sqrt(8^2 + 6^2) = 10`.
   5. 
      
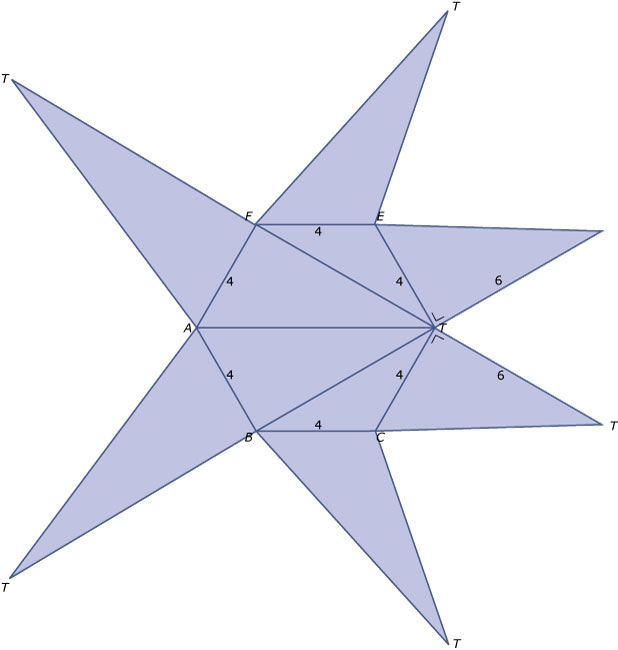
9. 1. Bij twijfel laten controleren.
   2. 
      
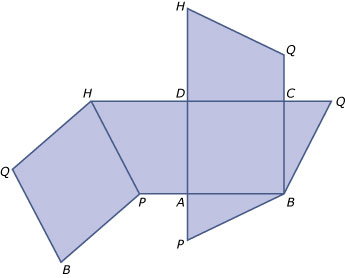
   3. Vlak `PBQH` is een ruit met zijden van `sqrt(6^2 + 3^2) = sqrt(45)` cm. Diagonaal `PQ = sqrt(72)` cm.
      Met behulp van goniometrie bereken je `/_PHQ = /_PBQ ~~ 78^o`. De andere twee hoeken zijn `102^o`.
10. 1. 
       
    2. 
       
11. Het grondvlak van de piramide bestaat uit vijf gelijkbenige driehoeken met een tophoek van `72^o` en een basis van 4 cm.
    De twee benen van deze driehoeken hebben een lengte van `AS = 2/(sin(36^o)) ~~ 3,4` cm. Dat is de straal van de cirkel waar de hoekpunten van vijfhoek `ABCDE` op liggen.
    De hoogte `TS` van de piramide bereken je bijvoorbeeld met behulp van de stelling van Pythagoras in `Delta AST`. Je vindt: `TS = sqrt(4^2 - AS^2) ~~ 2,1` cm.
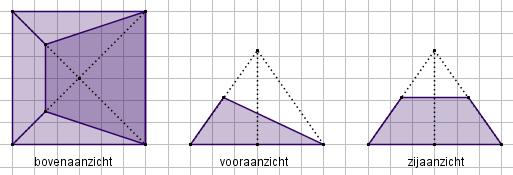
    Hiermee kun je de aanzichten tekenen.
12. De bovenkant is een kegel met hoogte 1 en straal grondcirkel 1,5 m.
    De onderkant is een afgeknotte kegel met straal grondcirkel 2 m en 1,5 m en hoogte 3 m. Deze afgeknotte kegel is afkomstig van een kegel met een hoogte van 12 m.
    
    
    
    
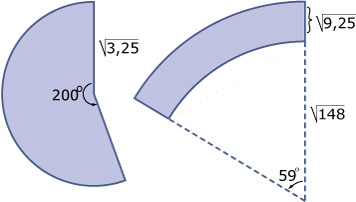
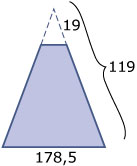13. De (stijve) kegelrok heeft de vorm van een afgeknotte kegel.
    De grondcirkel heeft een omtrek van `3/4 * 2pi * 119 = 178,5pi`. De straal van de grondcirkel is dus `89,25` cm.
    De bovencirkel heeft een omtrek van `3/4 * 2pi * 19 = 28,5pi`. De straal van de bovencirkel is dus `14,25` cm.
    Hiermee kun je de aanzichten tekenen. Eventueel kun je ook nog de hoogte van de afgeknotte kegel berekenen (`~~ 66,1` cm), maar nodig is dat niet. Het zijaanzicht zie je hiernaast.
14. Het bovenvlak en het ondervlak zijn regelmatige achthoeken. Die bestaan uit acht gelijkbenige driehoeken met een tophoek van `45^o` en een basis van 5 cm. De twee benen van deze driehoeken hebben een lengte van `(2,5)/(sin(22,5^o)) ~~ 6,5` cm. Dat is de straal van de cirkel waar de hoekpunten van deze achthoeken op liggen.
    De zijkant bestaat uit 16 gelijkzijdige driehoeken met zijden van 5 cm.
    
    
    
    
15. Het is alleen nodig om de hoogte van `T.ABCD` te berekenen, die is `sqrt(18)` cm. De rest kun je construeren met passer en liniaal.
    
    
    
    
    
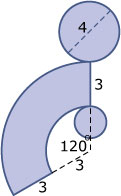16. Je moet alleen de sectorhoek berekenen met behulp van de omtrek van de grondcirkel van de afgeknotte kegel en de omtrek van de cirkel met straal 6 waar hij deel van is.