
Berekeningen
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Berekeningen > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Berekeningen > Inleiding
Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Zoek daartoe geschikte rechthoekige driehoeken en bedenk hoe de stelling van Pythagoras ook alweer ging en welke goniometrische verhoudingen je kent. Met de rechter muisknop kun je de figuur bewegen om beter de rechte hoeken te herkennen.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Berekeningen > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Berekeningen > Uitleg
Lees eerst de Uitleg goed door. Je vindt daar ook de antwoorden op de vragen die je bij Verkennen moest beantwoorden. Als je de stelling van Pythagoras en/of de goniometrische verhoudingen niet meer precies kent, kijk dan maar vast vooruit naar de Theorie.
Opgaven
-
Bekijk de balk `ABCD.EFGH` in de Uitleg.
- Welke vorm heeft vlak `AFGD` in werkelijkheid?
- Bereken de lengte van zijvlaksdiagonaal `AF`.
- Bereken de grootte van `/_AGF` in graden nauwkeurig.
-
Bekijk de balk `ABCD.EFGH` in de Uitleg. Punt `M` is het midden van ribbe `HG`.
- Bereken de lengte van `AM` en `BM`.
- Bereken de grootte van `/_AMH` in graden nauwkeurig.
- Bereken de grootte van `/_AMD` in graden nauwkeurig.
- Bereken de grootte van `/_AMB` in graden nauwkeurig.
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Berekeningen > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Berekeningen > Theorie
Bestudeer eerst de Theorie. In de opgaven word je naar de Voorbeelden verwezen.
Als je wordt gevraagd de grootte van een hoek te berekenen, ga er dan van uit dat je antwoord altijd in graden nauwkeurig moet zijn, tenzij anders wordt vermeldt.
Opgaven
-
In Voorbeeld 1 kun je zien hoe je lengtes van lijnstukken in ruimtelijke figuren berekent met behulp van de stelling van Pythagoras.
Gegeven is een balk `ABCD.EFGH` met `AB = 4`, `BC = 6` en `AE = 3`.
Punt `P` is het midden van `GH` en punt `Q` ligt op `CG` zo, dat `CQ = 1`.
- Bereken de lengte van `AP` en `AQ`.
- Onderzoek met behulp van de omgekeerde stelling van Pythagoras of `Delta AQP` rechthoekig is.
-
In Voorbeeld 2 zie je hoe je met behulp van de goniometrische verhoudingen de grootte van hoeken in ruimtelijke figuren kunt berekenen. Ook nu is het de kunst om de juiste rechthoekige driehoek te vinden.
Gebruik dezelfde balk met de punten `P` en `Q` uit de voorgaande opgave.
-
Bereken de grootte van `/_AFD`.
-
Bereken de grootte van `/_QAC`.
-
Welk probleem doet zich voor als je `/_PAQ` zou willen berekenen?
-
In Voorbeeld 3 zie je hoe je met gelijkvormige driehoeken kunt werken om lengtes te berekenen.
Gebruik dezelfde afgeknotte piramide.
-
Bereken de lengte van `EF`.
-
Bereken de grootte van `/_CBE`.
-
Van een driehoekig prisma `ABC.DEF` is het grondvlak `ABC` een gelijkzijdige driehoek met zijden van 4.
De hoogte `AD` van het prisma is ook 4. `P` is het midden van `DE`, `Q` is het midden van `EF`.
-
Bereken de lengte van de zijden van `Delta BPQ`.
-
Teken `Delta BPQ` op ware grootte en bereken de groottes van de hoeken van deze driehoek.
Verwerken
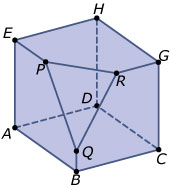 Je ziet hier een afgeknotte kubus met ribben van 6 cm. De punten `P` en `R` zijn de middens van de ribben waar ze op liggen.
`BQ = 1` cm.
Je ziet hier een afgeknotte kubus met ribben van 6 cm. De punten `P` en `R` zijn de middens van de ribben waar ze op liggen.
`BQ = 1` cm.
-
Bereken de lengtes van de zijden van `Delta PQR`.
-
Teken `Delta PQR` op ware grootte en bereken de hoeken van deze driehoek.
-
Het diagonaalvlak `DBQSH` is een vijfhoek.
Teken dit diagonaalvlak van de afgeknotte kubus op ware grootte en bereken de hoeken ervan.
-
Gegeven is een regelmatige piramide `T.ABCD` waarvan het vierkant `ABCD` het grondvlak is.
Alle ribben van deze piramide zijn 6 cm. `P` is het midden van `AT` en `Q` is het midden van `DT`.
`S` is het snijpunt van `AC` en `BD`.
- Bereken de hoogte `TS` van deze piramide.
- Leg uit waarom vierhoek `BCQP` een gelijkbenig trapezium is en bereken de lengtes van de zijden van deze vierhoek.
- Teken `BCQP` op ware grootte en bereken alle hoeken van dit trapezium.
-
Hieronder staan twee vlakke figuren. Bereken steeds de lengte van het lijnstuk waar het vraagteken bij staat.
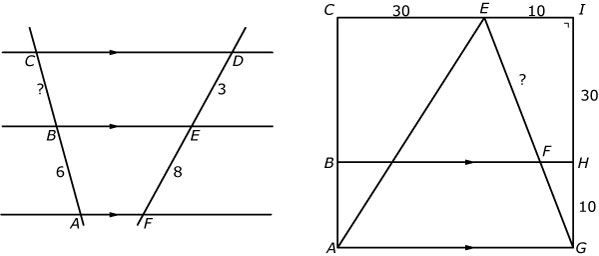
-
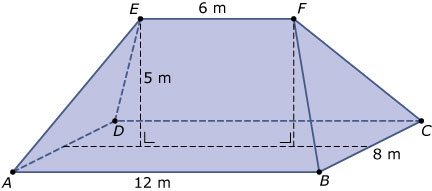
Je ziet hier een zogenaamd schilddak, een dakvorm met een rechthoekig grondvlak `ABCD` en waarbij de nok `EF` van het dak precies boven het midden van het grondvlak zit. Het dak zelf bestaat uit twee gelijkzijdige driehoeken en twee symmetrische trapezia.
-
Bereken de lengte van de ribben `AE, DE, BF` en `CF`.
-
Bereken de grootte van `/_ABF` en `/_BFC`.
-
Op 3 m boven de zoldervloer `ABCD` wordt een rechthoekige verdiepingsvloer aangebracht.
Bereken de oppervlakte van die verdiepingsvloer.
 Hiernaast zie je een foto van het gebouw "Willemswerf" in Rotterdam.
En hieronder zie je een bovenaanzicht van een sterk vereenvoudigde versie ervan.
Deze sterk vereenvoudigde versie in 80 m hoog.
De knik in het gebouw begint op 10 m boven het grondvlak. De knik in het gebouw heeft een grensvlak in de vorm van een trapezium.
Hiernaast zie je een foto van het gebouw "Willemswerf" in Rotterdam.
En hieronder zie je een bovenaanzicht van een sterk vereenvoudigde versie ervan.
Deze sterk vereenvoudigde versie in 80 m hoog.
De knik in het gebouw begint op 10 m boven het grondvlak. De knik in het gebouw heeft een grensvlak in de vorm van een trapezium.
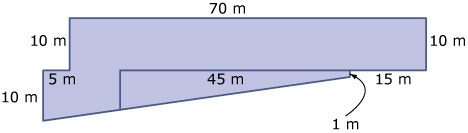
-
Bereken de lengtes van de zijden van dat trapezium.
-
Bereken de grootte van de hoeken van dat trapezium.
-
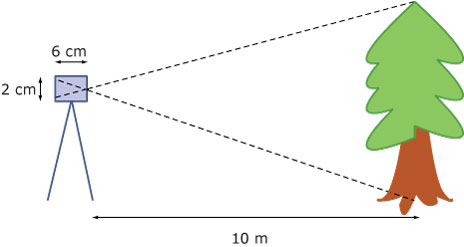
Marianne is een paar dagen in New York. Ze maakt een foto van een boom. Ze staat 10 m
van de boom vandaan. Op de foto is de boom 2 cm groot. De afstand van de lens tot
het negatief in het fototoestel is 6 cm.
-
Bereken nauwkeurig hoe hoog de boom is.
-
Na het ontwikkelen van de foto blijkt het vrijheidsbeeld ook op de foto te staan.
Toevallig is op de foto het vrijheidsbeeld precies even groot als de boom.
Het vrijheidsbeeld is 93 m hoog. Hoe ver stond Marianne van het vrijheidsbeeld vandaan?
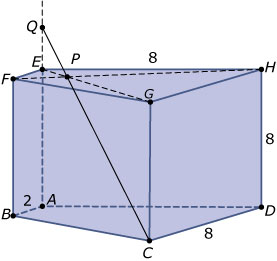 Je ziet hier een aan de voorkant afgeknotte kubus `ABCD.EFGH`. `/_BAD = /_ADC = 90^o`. De afmetingen staan
in de figuur. Bereken de lengte van `AQ`.
Je ziet hier een aan de voorkant afgeknotte kubus `ABCD.EFGH`. `/_BAD = /_ADC = 90^o`. De afmetingen staan
in de figuur. Bereken de lengte van `AQ`.
Testen
-
Van een regelmatige vierzijdige piramide `T.ABCD` is het grondvlak `ABCD` een vierkant
met zijde 4. `S` is het snijpunt van de diagonalen `AC` en `BD` en `TS = 10`. Punt `M` is het
midden van `TS`.
-
Teken deze piramide in parallelprojectie.
Teken een lijn door `M` evenwijdig aan `BD`. Noem de snijpunten met `TB` en `TD` respectievelijk `P` en `Q`.
-
Bereken de lengte van `AP` en `PQ`.
-
Teken `Delta APQ` op ware grootte en bereken de hoeken van deze driehoek.

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Berekeningen > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Berekeningen > Inleiding![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Berekeningen > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Berekeningen > Uitleg![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Berekeningen > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Berekeningen > Theorie Je ziet hier een afgeknotte kubus met ribben van 6 cm. De punten `P` en `R` zijn de middens van de ribben waar ze op liggen.
`BQ = 1` cm.
Je ziet hier een afgeknotte kubus met ribben van 6 cm. De punten `P` en `R` zijn de middens van de ribben waar ze op liggen.
`BQ = 1` cm.


 Hiernaast zie je een foto van het gebouw "Willemswerf" in Rotterdam.
En hieronder zie je een bovenaanzicht van een sterk vereenvoudigde versie ervan.
Deze sterk vereenvoudigde versie in 80 m hoog.
De knik in het gebouw begint op 10 m boven het grondvlak. De knik in het gebouw heeft een grensvlak in de vorm van een trapezium.
Hiernaast zie je een foto van het gebouw "Willemswerf" in Rotterdam.
En hieronder zie je een bovenaanzicht van een sterk vereenvoudigde versie ervan.
Deze sterk vereenvoudigde versie in 80 m hoog.
De knik in het gebouw begint op 10 m boven het grondvlak. De knik in het gebouw heeft een grensvlak in de vorm van een trapezium.

 Je ziet hier een aan de voorkant afgeknotte kubus `ABCD.EFGH`. `/_BAD = /_ADC = 90^o`. De afmetingen staan
in de figuur. Bereken de lengte van `AQ`.
Je ziet hier een aan de voorkant afgeknotte kubus `ABCD.EFGH`. `/_BAD = /_ADC = 90^o`. De afmetingen staan
in de figuur. Bereken de lengte van `AQ`.