Berekeningen

Antwoorden bij de opgaven

1. 1. Een rechthoek.
   2. `sqrt(5^2 + 2^2) = sqrt(29)`
   3. `tan(/_AGF) = (AF)/(FG) = (sqrt(29))/3`, dus `/_AGF ~~ 61^o`.
2. 1. `AM = BM = sqrt(AH^2 + HM^2) = sqrt(3^2 + 2^2 + 2,5^2) = sqrt(29,25)`
   2. `tan(/_AMH) = (AH)/(HM) = (sqrt(13))/(sqrt(6,25))`, dus `/_AMH ~~ 55^o`.
   3. `sin(/_AMD) = (AD)/(AM) = (3)/(sqrt(19,25))`, dus `/_AMD ~~ 43^o`.
   4. `/_AMB = 180^o - 2 * /_AMH ~~ 69^o`
3. 1. `AP = sqrt(AH^2 + HP^2) = sqrt(6^2 + 3^2 + 2^2) = sqrt(49) = 7`
      `AQ = sqrt(AB^2 + BQ^2) = sqrt(4^2 + 6^2 + 1^2) = sqrt(53)`
   2. `PQ = sqrt(2^2 + 2^2) = sqrt(8)` en dus is `AQ^2 != AP^2 + PQ^2`.
4. 1. `tan(/_AFD) = (AD)/(AF) = (6)/(5)`, dus `/_AFD ~~ 50^o`.
   2. `sin(/_CAQ) = (CQ)/(AQ) = (1)/(sqrt(53))`, dus `/_AMD ~~ 8^o`.
   3. `Delta PAQ` is niet rechthoekig.
5. 1. `CT = 12`, `TF = 12 - 3 = 9` en `CB = 3`.
      `Delta TCB` is gelijkvormig met `Delta TFE`.
      Dus `FE = 9/12 * CB = 9/12 * 3 = 2,25`.
   2. `tan(/_CBE) = 12/3 = 4` dus `/_CBE ~~ 72^o`.
6. 1. `PQ = 2` en `BP = BQ = sqrt(4^2 + 2^2) = sqrt(20)`
   2. `cos(/_BPQ) = 1/(sqrt(20))`, dus `/_BPQ ~~ 77^o`. En `/_BQP = /_BPQ = 77^o`.
      Dus is `/_PBQ = 180^o - 2 * /_BPQ ~~ 36^o`.
7. 1. `PR = sqrt(18)` en `QP = QR = sqrt(34)`
   2. `/_QPR = /_QRP ~~ 69^o` en `/_PQR ~~ 43^o`.
   3. Teken eerst rechthoek `DBFH` met `DB = HF = sqrt(72) ~~ 8,5` en `DH = BF = 6` cm.
      Vervolgens teken punt `Q` zo, dat `BQ = 1` en punt `S` zo, dat `FS = 1/4 * HF`.
      Nu kun je vijfhoek `DBQSH` tekenen.
      Deze vijfhoek heeft twee hoeken van `90^o`, een hoek van `157^o` en een hoek van `117^o`.
8. 2. `TS = sqrt(18)`
   3. `BC` en `PQ` lopen evenwijdig en `BP = CQ`.
      `BP = CQ = sqrt(27)`, `BC = 6` en `PQ = 3` cm.
   4. Om de figuur te kunnen tekenen is het verstandig om eerst de hoogte van het trapezium uit te rekenen. Die hoogte is `sqrt(18 - 1,5^2) = sqrt(15,75) ~~ 4,0` cm.
      Het trapezium heeft twee hoeken van ongeveer `69^o` en twee hoeken van ongeveer `111^o`.
9. 1. `BC = 3/11 * 6 = 18/11`
   2. `EG = sqrt(1700)` en `EF = 3/4 * sqrt(1700)`.
10. 1. `AE = DE = BF = CF = sqrt(50)`
    2. `/_ABF ~~ 65^o` en `/_BCF ~~ 68^o`.
    3. De breedte van de verdiepingsvloer is `2/5 * 8 = 3,2` m.
       De lengte van de verdiepingsvloer is `6 + 2 * 2/5 * 3 = 8,4` m.
       De oppervlakte is daarom `3,2 * 8,4 = 26,88` m².
11. 
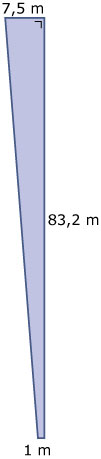
    1. Hiernaast zie je het bedoelde (rechthoekige) trapezium.
       De zijde waar `83,2` m bij staat heeft een preciese lengte van `sqrt(45^2 + 70^2) = sqrt(6925)`.
       De langste zijde van het trapezium is `sqrt(6925 + 6,5^2) = sqrt(6967,25) ~~ 83,5` m.
    2. Behalve twee rechte hoeken is er een hoek van ongeveer `86^o` en een hoek van ongeveer `94^o`.
12. 1. Als `h` de hoogte van de boom is, dan is `6/1000 * h = 2` cm.
       Dus is `h = 2000/6 ~~ 333,3` cm. Het is daarom maar een klein boompje van ongeveer 3,33 m.
    2. Als `a` de afstand tot het vrijheidsbeeld is geldt: `6/a * 9300 = 2`. Dit betekent `a = 27900` cm, dat is 279 m.
13. `(EQ)/(AQ) = (EP)/(AC) = (EP)/(EQ) = (EF)/(GF) = 2/8`.
    Neem `AQ = x`, dan is `EQ = x - 8`. Dus is `(x - 8)/x = 2/8`. Dit levert op `AQ = x = 10 2/3`.
14. 1. -
    2. `AS = sqrt(8)` en `SM = 5` geeft `AM = sqrt(33)`.
       Nu is `MP = MQ = 1/2 * sqrt(8) = sqrt(2)` en `Delta AMP` en `Delta AMQ` zijn rechthoekig.
       `AP = AQ = sqrt(35)`.
    3. `tan(/_APM) = (sqrt(33))/(sqrt(2)`, dus `/_APM ~~ 76^o`. Dit betekent dat `/_AQM ~~ 76^o` en `/_PAQ ~~ 28^o`.