Projectie op het platte vlak

Antwoorden bij de opgaven

1. 1. Een rechthoek.
   2. `BC, EH, FG`
   3. `BD ~~ 5,7` cm
   4. `DF ~~ 6,9` cm
   5. Laat bij twijfel je figuur controleren.
2. Nee, omdat de ribben die schuin naar achteren lopen niet zijn verkort is dit een parallelprojectie van een balk.
3. Laat bij twijfel je figuur controleren.
4. Laat bij twijfel je figuur controleren.
5. 1. `BP ~~ 4,5` cm
   2. Alle zijden zijn even lang.
   3. `PQ = AC ~~ 5,7` cm.
   4. Begin met `PQ = 5,7` cm. Neem vervolgens `BP = 4,5` cm tussen de passerpunten.
      Cirkel `PB, QB, PC` en `QC` met de passer om.
      Je vindt nu de punten `B` en `C` en je kunt de ruit tekenen.
6. 1. 
   2. 
   3. 
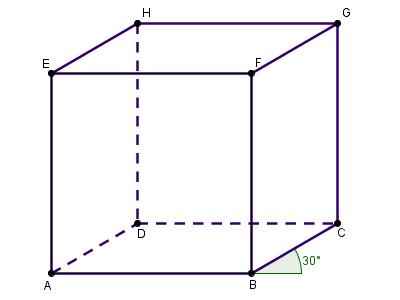
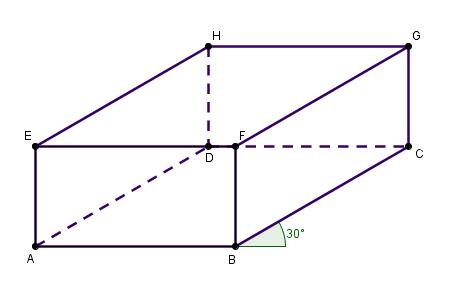
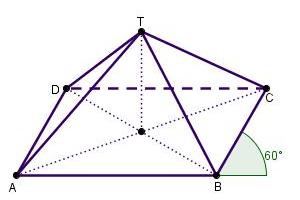
7. 1. Er is geen verkortingsfactor gegeven, dus het is verstandig om van het rooster gebruik te maken.
      
      
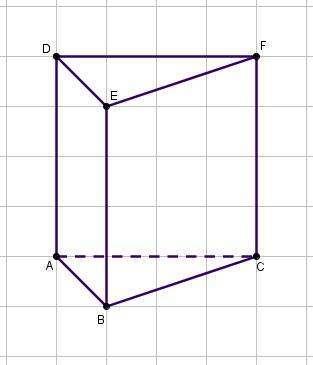
   2. `Delta PQR` wordt een driehoek met `PR = 2` en `PQ = QR ~~ 2,8`.
8. 1. 
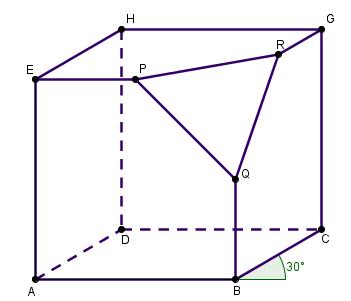
   2. `Delta PQR` wordt een gelijkzijdige driehoek met zijden van 4,2 cm.
   3. Teken eerst rechthoek `DBFH` met `DB = HF ~~ 8,5` en `DH = BF = 6` cm.
      Vervolgens teken je het midden `Q` van `BF` en punt `S` zo, dat `FS = 1/4 * HF`.
      Nu kun je vijfhoek `DBQSH` tekenen.
9. 
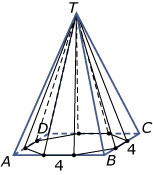
   1. Zie figuur.
   2. Zie figuur. Je verdeelt gewoon elke zijde in drie gelijke delen door opmeten. Dat mag omdat de figuur een parallelprojectie is.
   3. Zie figuur.
   4. Nee, het grondvlak is geen achthoek met gelijke zijden. Er zijn zijden van 2 cm en zijden van 2,8 cm.
10. 1. 
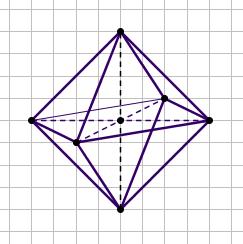
    2. Het worden gelijkzijdige driehoeken met zijden van ongeveer 5,7 cm.
    3. Dat levert een kubus op.
11. 1. Bij twijfel laten controleren.
    2. De beide driehoeken hebben een basis van 8 cm en een hoogte van ongeveer 5,8 cm.
       Die hoogte is het lijnstuk vanuit `F` naar het midden `N` van `BC` of het lijnstuk vanuit `E` naar het midden `M` van `AD`. Als je `EMNF` op ware grootte tekent kun je die hoogtes meten.
    3. De hoogte van zo'n trapezium is ongeveer 6,4 cm.
       Je meet die hoogte in een driehoek door `E` of `F` en evenwijdig met `BC`.
12. 
    1. 
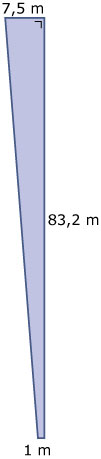
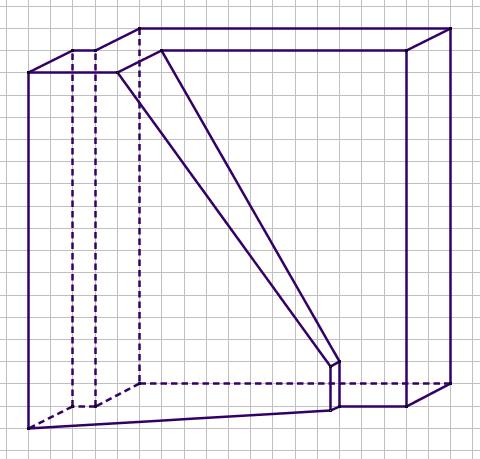
    2. Je ziet het bedoelde trapezium hiernaast.
13. 1. 
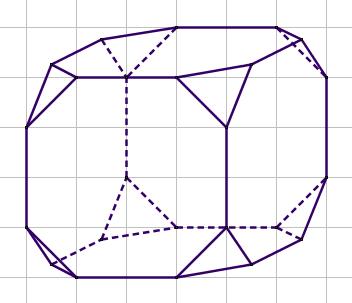
    2. Zo'n grensvlakje is een gelijkzijdig driehoekje met zijden van ongeveer 1,4 cm.
14. Bij twijfel laten controleren.