Toepassingen

Antwoorden bij de opgaven

1. Het blik is zuiver cilindervormig en het materiaal is overal even dik zodat de hoeveelheid materiaal alleen wordt bepaald door de oppervlakte ervan.
2. Oppervlakte van twee cirkels (bovenkant en onderkant) met straal `r` en één rechthoek (de cilindermantel) met hoogte `h` en breedte `2pi r`.
3. -
4. `A'(r) = (-2000)/(r^2) + 4pi r = 0` geeft `r^3 = (2000)/(4pi)` en dus `r ~~ 5,42`.
1. -
2. Het blauwe streepjeslijntje is `A(x)`. Ga na dat de rechthoekige driehoek met rechthoekszijden `x - 1` en `A(x)` gelijkvormig is met de grotere rechthoekige driehoek met zijden `x` en `sqrt(2,5^2 - x^2)`. Daaruit volgt: `(x - 1)/x = (A(x))/(sqrt(2,5^2 - x^2))`.
3. `A(x) = (1 - 1/x)sqrt(2,5^2 - x^2)` geeft `A'(x) = 1/(x^2) * sqrt(2,5^2 - x^2) + (1 - 1/x) * (-x)/(sqrt(2,5^2 - x^2))`.
  `A'(x) = 0` levert op `(sqrt(2,5^2 - x^2))/(x^2) = (x - 1)/(sqrt(2,5^2 - x^2))` en dus `x^3 - x^2 = 2,5^2 - x^2` en `x^3 = 6,25` zodat `x = root[3](6,25) ~~ 1,84`.
  Ga na dat er inderdaad van een maximum sprake is.
1. -
2. Zie Voorbeeld 2.
3. Omdat `T(x) = t(30 - x + 1,5sqrt(x^2 + 100)) = t * A(x)` (en `t > 0`) is `T` minimaal als `A` dat is.
  `A'(x) = -1 + (1,5x)/(sqrt(x^2 + 100)) = 0` geeft `sqrt(x^2 + 100) = 1,5x` en na kwadrateren `1,25x^2 = 100`.
  Dit betekent dat `A` (en dus `T`) minimaal is als `x = sqrt(80) ~~ 8,94` m.
  Het antwoord op de in het voorbeeld gestelde vraag is dat er `21,06` m langs de wegkant moet worden gegraven en vandaar rechtsreeks door de tuin naar het woonhuis.
1. -
2. `DA = BC = 20` en dus is de hoogte van het trapezium `20 sin(alpha)`.
  Het trapezium bestaat uit een rechthoek van `20` bij `20 sim(alpha)` en twee driehoeken die samen een rechthoek vormen van `20 cos(alpha)` bij `20 sin(alpha)`. De totale oppervlakte van het trapezium is `A(alpha) = 20 * 20 sin(alpha) + 20 cos(alpha) * 20 sin(alpha)`.
3. `A'(alpha) = 400 cos(alpha) + 400 cos^2(alpha) - 400 sin^2(alpha) = 0` als `alpha = 1/3 pi` (gebruik je grafische rekenmachine om deze vergelijking op te lossen).
De lengte van `AB` is `L(p) = sqrt(p) - p^2`.
`L'(p) = 1/(2sqrt(p)) - 2p = 0` geeft `4p sqrt(p) = 1` en dus `p^3 = 1/(16)`.
De lengte van `AB` is maximaal als `p = root[3](1/16) ~~ 0,40`.
1. -
2. -
3. `A(x) = (x - 2)(100/x - 3)`
4. `A'(x) = -3 + (200)/(x^2) = 0` geeft `x^2 = 200/3` en dus `x ~~ 8,2` dm.
5. De poster moet ongeveer 8,2 bij 12,2 dm worden.
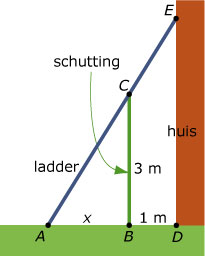`Delta ABC` is gelijkvormig met `Delta ADE`, dus `x/(x+1) = 3/(DE)` zodat `DE = (3x + 3)/x = 3 + 3/x`.
De lengte van de ladder is `L(x) = sqrt((x + 1)^2 + (3 + 3/x)^2)`.
Met behulp van differentiëren bepaal je nu het minimum van `l(x) = (x + 1)^2 + (3 + 3/x)^2`.
Je vindt een minimale lengte van 7,56 m.
Noem de basis van de gelijkbenige driehoek `x`, dan zijn de benen elk `10 - 1/2 x`.
De oppervlakte is dan `A(x) = 1/2 x sqrt((10 - 1/2 x)^2 - (1/2 x)^2) = 1/2 x sqrt(100 - 10x)`.
`A'(x) = 1/2 sqrt(100 - 10x) - (2,5x)/(sqrt(100 - 10x)) = 0` geeft `100 - 10x = 5x` en dus `x = 6 2/3`.
De zijden zijn dus alle drie `6 2/3` cm.
1. Maak een schets van de situatie.
2. `A'(k) = sqrt(10 - 2k) - k/(sqrt(10 - 2k)) = 0` geeft `sqrt(10 - 2k) = k/(sqrt(10 - 2k))` en `10 - 2k = k` zodat `k = 3 1/3`.
1. Als `p = 1` is `f(x) = (x^2 + 1)/(x) = x + 1/x`.
  `f'(x) = 1 - 1/x^2 = 0` geeft `x^2 = 1` en dus `x = -1 vv x = 1`. Extremen max.`f(-1) = -2` en min.`f(1) = 2`.
2. `f'(x) = 1 - p/(x^2) = 0` geeft `x^2 = p`.
  Er zijn geen oplossingen als `p < 0` en ook als `p=0` zijn er geen extremen.
3. `f'(0) = 1 - p/(x^2)` en `f'(2) = 1 - p/4 = -1` geeft `p = 8`.
1. De lengte van `OP` is `L(p) = sqrt(p^2 + (4 - p^2)^2) = sqrt(p^4 - 7p^2 + 16)`.
  `L(p)` is minimaal als `l(p) = p^4 - 7p^2 + 16` dat is.
  `l'(p) = 4p^3 - 14p = 0` als `p = 0 vv p = +-sqrt(3,5)`.
  De minimale lengte van lijnstuk `OP` is `L(+-sqrt(3,5)) = sqrt(3,75)`.
2. De oppervlakte van rechthoek `APQB` is `A(p) = 2p(4 - p^2) = 8p - 2p^3`.
  `A'(p) = 8 - 6p^2 = 0` als `p = +-sqrt(4/3)`.
  De maximale oppervlakte is `5 1/3 sqrt(4/3)`.
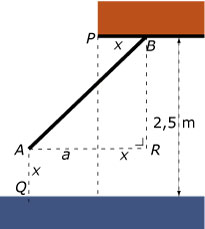Zie figuur: van `a(x)` is het maximum te berekenen.
Doe de stelling van Pythagoras in `Delta ARB`: `(a + x)^2 + (2,5 - x)^2 = 2,5^2`.
Dit levert op `a(x) = -x + sqrt(5x - x^2)`.
`a'(x) = -1 + (5 - 2x)/(2 sqrt(5x - x^2)) = 0` geeft `x = (5 +- sqrt(5))/2`.
`a` is maximaal als `x = (5 - sqrt(5))/2 ~~ 1,38` en `a(1,38) ~~ 0,85` m.
1. `f'(x) = 4(x^2 - x)^3(2x - 1) = 0` geeft `x = 0 vv x = 1 vv x = 1/2`.
  Je vindt min.`f(0) = f(1) = 0` en max.`f(1/2) = 1/256`.
2. De oppervlakte van de beschreven driehoek is `A(k) = 1/2 k(k^2 - k)^4`.
  `A'(k) = 1/2(k^2 - k)^4 + 2k(k^2 - k)^3(2k - 1) = 1/2(k^2 - k)^3(9k^2 - 5k) = 0` geeft `k = 0 vv k = 1 vv k = 5/9`.
  De bedoelde oppervlakte is maximaal als `k = 5/9`.