
De afgeleide van een sinusoïde
Inleiding
Als je met sinusoïden hebt gewerkt, dan weet je dat het hierbij gaat om functies die door transformatie kunnen ontstaan uit de grafiek van y = sin(x) of y = cos(x). Een sinusoïde beschrijft een periodiek verschijnsel. De hellingwaarden van een sinusoïde veranderen daarom ook periodiek.
Niet zo vreemd dus, dat de afgeleide van een sinusoïde ook zelf weer een sinusoïde is.
Je leert nu:
- de afgeleide van een sinusoïde bepalen;
- de differentieerregels toepassen op functies waarin sinus, cosinus of tangens voorkomen.
Je kunt al:
- werken met sinusoïden;
- de differentieerregels gebruiken;
- werken met de afgeleide onder andere voor het berekenen van extremen.
Verkennen
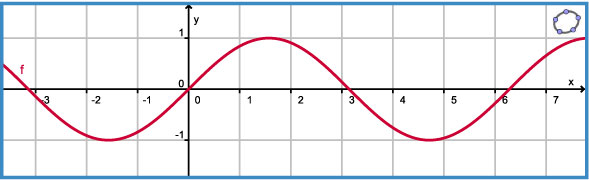
Je ziet hier een deel van de grafiek van f(x) = sin(x).
> Schets de bijbehorende hellinggrafiek. Welke functie hoort er bij die hellinggrafiek?
> Welke functie is de afgeleide van f(x) = sin(x)?
Uitleg
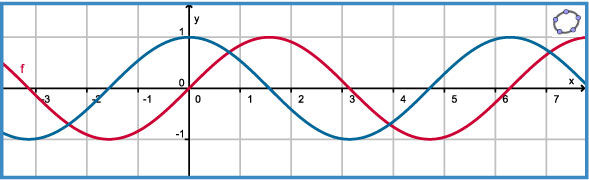
Je ziet hier de grafiek van f(x) = sin(x).
Je ziet ook de grafiek van de afgeleide in beeld.
Uit de figuur lijkt te volgen: f'(x) = cos(x).
De afgeleide van f(x) = sin(x) is f'(x) = cos(x).
Zo kun je ook de grafiek van g(x) = cos(x) bekijken.
De grafiek van de afgeleide lijkt op die van: g'(x) = –sin(x).
De afgeleide van g(x) = cos(x) is g'(x) = –sin(x)
‡
Opgaven
-
Bekijk in bij Verkennen de grafiek van `f(x) = sin(x)` met op beide assen dezelfde schaalverdeling.
- Teken in de grafiek de raaklijn voor `x = 0` en ga na dat de bijbehorende hellingswaarde inderdaad ongeveer 1 is.
- Voor welke waarden van `x` is de helling nog meer 1? En waar is hij `-1`?
- Voor welke waarden van `x` is de helling 0?
- Teken met je grafische rekenmachine de grafiek van `f(x) = sin(x)` en de bijbehorende hellingsgrafiek. Ga na, dat die hellingsgrafiek samenvalt met de grafiek van `y = cos(x)`.
-
Teken zelf (of in GeoGebra) de grafiek van `g(x) = cos(x)`.
- Teken in de grafiek de raaklijn voor `x = 0` en ga na dat de bijbehorende hellingswaarde inderdaad ongeveer 1 is.
- Voor welke waarden van `x` is de helling nog meer 1? En waar is hij `-1`?
- Voor welke waarden van `x` is de helling 0?
- Teken met je grafische rekenmachine de grafiek van `f(x) = sin(x)` en de bijbehorende hellingsgrafiek. Ga na, dat die hellingsgrafiek samenvalt met de grafiek van `y = cos(x)`.
-
Je weet nu hoe je de functie `f(x) = sin(x)` moet differentiëren. Daarnaast ken je alle basisregels voor het differentiëren.
Differentieer nu de volgende functies.
-
`f_1(x) = sin(x) + 2`
-
`f_2(x) = sin(x + 2)`
-
`f_3(x) = 2 sin(x)`
-
`f_4(x) = sin(2x)`
Theorie
Het differentiëren van functies waarin sinus en/of cosinus voorkomen is gebaseerd op:
- de afgeleide van f(x) = sin(x) is f'(x) = cos(x)
- de afgeleide van f(x) = cos(x) is f'(x) = –sin(x)
Om de afgeleide van een functie waarin sinus en/of cosinus voorkomen te bepalen heb je ook vaak nog de overige differentieerregels nodig.
Bijvoorbeeld moet je bij afgeleide van een sinusoïde rekening houden met de kettingregel en met de constante-regels. (Zie Voorbeeld 1.)
‡
Voorbeeld 1
Gegeven is de functie f(x) = –10 + 20 sin(0,1πx – 0,2π) met domein [–10, 10].
Stel m.b.v. differentiëren een vergelijking op van de raaklijn aan de grafiek van f voor x = 0.
Antwoord
f'(x) = 20 cos(0,1πx – 0,2π) · 0,1π = 2π cos(0,1πx – 0,2π).
Daaruit volgt: f'(0) = 2π cos(– 0,2π) ≈ 5,08.
Verder is: f(0) = –10 + 20 sin(– 0,2π) ≈ –21,76.
De vergelijking van de raaklijn wordt: y = 5,08x – 21,76.
‡
Voorbeeld 2
Bij het in- en uitademen varieert het longvolume L (in liters) periodiek met de tijd t (in seconden). Stel je voor dat iemand's longvolume varieert tussen 3,05 en 3,15 L en dat deze persoon 40 keer per minuut in- en uitademt. Neem verder aan dat L(t) een zuivere sinusoïde is.
Op t = 0 is zijn longvolume maximaal. Bereken de grootste snelheid van uitademen.
Antwoord
Dit is een passende formule: L(t) = 3,10 + 0,05 cos(x).
Hierin is t in seconden (er gaan 40 ademhalingen in 60 seconden, dus de periode is 1,5 sec.).
De grootste snelheid van uitademen vindt plaats als de grafiek de evenwichtsstand passeert vanaf een maximum naar een minimum. Bijvoorbeeld op t = 1,5/4 = 0,375.
Die snelheid is dan gelijk aan de afgeleide van L(t) op dat tijdstip.
Nu is: L'(t) = –0,05 sin(t) · .
En daarom is: L'(0,375) = –0,05 sin( · 0,375) · ≈ –0,021.
De maximale snelheid van uitademen in ongeveer 0,021 L/s.
‡
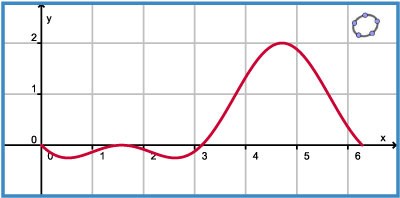
Voorbeeld 3
Je ziet hier de grafiek van een functie f van de vorm f(x) = sin2(x) – p sin(x) voor p = 1. Het domein van deze functie is [0,2π]. Als p = 1 heeft de grafiek van f vier extremen.
Voor welke waarden van p heeft de grafiek van f vier extremen?
Antwoord
f'(x) = 2 sin(x) cos(x) – p cos(x) = 0 geeft:
cos(x)(2 sin(x) – p) = 0
en dus:
cos(x) = 0 V sin(x) = 0,5p.
Op [0,2π] heeft cos(x) = 0 twee oplossingen.
Dan moet dit ook gelden voor sin(x) = 0,5p.
Dit betekent –1 < 0,5p < 1 en p ≠ 0.
Dus moet –2 < p < 2 en p ≠ 0.
‡
Opgaven
-
In Voorbeeld 1 zie je hoe je de afgeleide van een sinusoïde bepaalt.
Differentieer nu zelf de volgende functies.
- `f(x) = 4 sin(2x)`
- `f(x) = 100 + 10 sin(0,5(x - 5))`
- `f(x) = 20 - 15 cos((pi)/(6)(x + 1))`
- `H(t) = 8 sin((2pi)/(15)t) + 4`
-
Gegeven is de functie `f` door `f(x) = 20 + 6 sin((pi)/(6)(x - 2))`.
-
Bepaal van deze functie de afgeleide.
-
Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x = 4`.
-
In welke punten van de grafiek van `f` is de richtingscoëfficiënt van de raaklijn zo groot mogelijk? Hoe groot is die richtingscoëfficiënt?
-
Voorbeeld 2 gaat over het longvolume van een mens bij het in- en uitademen. Ga weer uit van een maximaal longvolume op `t = 0`.
-
Leg uit hoe je aan de formule voor `L` komt. Gebruik de begrippen periode, amplitude, evenwichtsstand.
-
Hoeveel bedraagt zijn longvolume op `t = 1`?
-
Hoeveel bedraagt de snelheid waarmee het longvolume verandert op `t = 1`? Gaat het dan om inademen of uitademen?
-
Op welke tijdstippen is de snelheid van de uitstromende lucht maximaal?
-
Differentieer de volgende functies.
- `f(x) = 2 sin(x) + cos(2x) + 3`
- `f(x) = sin^2(x)`
- `f(x) = cos^2(x) + 3 cos(x)`
- `f(x) = cos^2(3x)`
- `f(x) = (sin(x))/(cos(x))`
-
Bekijk Voorbeeld 3. Het gaat daar om een familie van functies van de vorm `f(x) = sin^2(x) - p sin(x)` op `[0,2pi]`.
- Neem `p = -1`. Om welke functie `f` gaat het nu? Bereken van deze functie alle extremen.
- Bij elke waarde van `p` heeft de grafiek van `f` een top in `A(1/2 pi,f(1/2 pi))` en een top in `B(1 1/2 pi,f(1 1/2 pi))`. Toon dit aan.
- Er zijn twee waarden van `p` waarvoor het punt `A` tweemaal zover van de `x`-as ligt als het punt `B`. Bereken die waarden van `p`.
Verwerken
- Differentieer de volgende functies.
- `f(x) = 3 sin(2x)`
- `g(x) = 16 - 20 cos((2pi)/(30)(x - 5))`
- `H(t) = sin^2(440pi t)`
- `y(x) = sqrt(16 + sin^2(x))`
- `A(r) = 1/(sin(2r))`
- `W(p) = 2 sin(p) cos(2p)`
-
Bekijk de grafiek van de functie `f` met `f(x) = 3 cos(2x) + 1` op `[0,2pi]`.
- Bereken algebra´sch de uiterste waarden van `f`.
- Los algebraïsch op: `f(x) < 2,5` .
- De lijn `y = 2,5` snijdt de grafiek van `f` in vier punten. Bereken de hellingswaarden in die punten.
-
In een bepaald gebied waar eb en vloed heerst wordt de waterhoogte `H` (in m t.o.v. NAP) op tijdstip `t` (in uren) beschreven door `H(t) = 2 cos((2pi)/(12,25)(t - 3)) + 1`.
Hierin is `t = 0` op 0:00 uur van een bepaalde dag.
- Bereken de waterhoogte om 0:00 uur.
- Bereken met behulp van differentiŰren de tijdstippen van hoogwater die dag. Waarom is hierbij differentiëren eigenlijk niet nodig?
- Bereken H'(4). Welke betekenis heeft dit getal voor het verloop van de waterhoogte?
- Op welke tijdstippen verandert de waterstand het snelst?
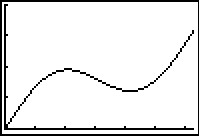 Hier zie je het deel van de grafiek van `f(x) = 0,5x + sin(x)` met `0 <= x <= 2pi`.
Hier zie je het deel van de grafiek van `f(x) = 0,5x + sin(x)` met `0 <= x <= 2pi`.
- Bereken met behulp van differentiëren de twee extremen van `f`.
- Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x = 0`.
- Bereken het punt op de grafiek van `f` waarin de raaklijn het kleinste hellingsgetal heeft en bereken dit hellingsgetal.
-
Bekijk de grafiek van de functie `f` met `f(x) = sin(x^2)`.
Hoeveel extremen heeft deze functie op het interval `[2pi, 3pi]`?
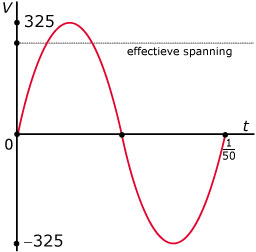 Het vermogen `P` van door energiemaatschappijen geleverde wisselstroom is recht evenredig met het kwadraat van de spanning `V` (in Volt).
Men levert wisselstroom met een effectieve spanning van 230 V, een frequentie van 50 Herz (dat is 50 periodes per seconde) en een amplitudo van ongeveer 325 V.
De spanning `V` als functie van de tijd `t` is een zuivere sinuoïde.
Het vermogen `P` van door energiemaatschappijen geleverde wisselstroom is recht evenredig met het kwadraat van de spanning `V` (in Volt).
Men levert wisselstroom met een effectieve spanning van 230 V, een frequentie van 50 Herz (dat is 50 periodes per seconde) en een amplitudo van ongeveer 325 V.
De spanning `V` als functie van de tijd `t` is een zuivere sinuoïde.
- Stel een formule op voor `V(t)` uitgaande van `V(0)=0`.
- Voor het vermogen `P` geldt: `P(t) = sin^2(100pi t)`. Welke waarde heeft de evenredigheidsconstante in dit geval?
- Bereken algebraïsch de toppen en de nulpunten van `P`.
- De grafiek van `P` is een zuivere sinusoïde. Geef een formule voor die sinusoïde.
Testen
- Differentieer de volgende functies.
- `f(x) = 2 cos(3x)`
- `u(t) = 1,5 sin(220pi (t - 1))`
- `g(x) = x^2 cos(x)`
- `y(t) = 5 cos(0,5pi t - pi) + 0,15t + 2`
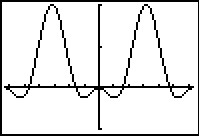 Je ziet hier de grafiek van de functie `f(x) = cos^2(x) - cos(x)` op `[-2pi, 2pi]`.
Je ziet hier de grafiek van de functie `f(x) = cos^2(x) - cos(x)` op `[-2pi, 2pi]`.
- Bereken met behulp van de afgeleide de extremen van `f`.
- Het punt `(1/2 pi,0)` ligt op de grafiek van `f`. Laat zien dat dit inderdaad het geval is. Stel een vergelijking op van de raaklijn aan de grafiek van `f` in dat punt.
-
Het tijdstip van de dagelijkse zonsopkomst verandert in loop van het jaar.
In een bepaald jaar was het vroegste tijdstip van zonsopkomst 4:20 uur op 21 juni en het laatste tijdstip van zonsopkomst 8:50 op 21 december.
Noem het tijdstip van zonsopkomst `Z` en de dag in het jaar `t` met `t = 0` op 1 januari (om 0:00 uur).
- Stel een formule op voor `Z(t)` voor dat jaar.
- Bereken met behulp van de afgeleide de dagen waarop het tijdstip van zonsopkomst het snelst veranderde dat jaar.
 Het vermogen `P` van door energiemaatschappijen geleverde wisselstroom is recht evenredig met het kwadraat van de spanning `V` (in Volt).
Men levert wisselstroom met een effectieve spanning van 230 V, een frequentie van 50 Herz (dat is 50 periodes per seconde) en een amplitudo van ongeveer 325 V.
De spanning `V` als functie van de tijd `t` is een zuivere sinuoïde.
Het vermogen `P` van door energiemaatschappijen geleverde wisselstroom is recht evenredig met het kwadraat van de spanning `V` (in Volt).
Men levert wisselstroom met een effectieve spanning van 230 V, een frequentie van 50 Herz (dat is 50 periodes per seconde) en een amplitudo van ongeveer 325 V.
De spanning `V` als functie van de tijd `t` is een zuivere sinuoïde.



