
De afgeleide van een sinusoïde
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Differentieerregels > Afgeleide sinusoïde > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Differentieerregels > Afgeleide sinusoïde > Inleiding
Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Differentieerregels > Afgeleide sinusoïde > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Differentieerregels > Afgeleide sinusoïde > Uitleg
Lees eerst in de Uitleg wat de afgeleiden zijn van `f(x) = sin(x)` en `g(x) = cos(x)`.
(Denk om `x` in radialen!)
Opgaven
-
Bekijk in bij Verkennen de grafiek van `f(x) = sin(x)` met op beide assen dezelfde schaalverdeling.
- Teken in de grafiek de raaklijn voor `x = 0` en ga na dat de bijbehorende hellingswaarde inderdaad ongeveer 1 is.
- Voor welke waarden van `x` is de helling nog meer 1? En waar is hij `-1`?
- Voor welke waarden van `x` is de helling 0?
- Teken met je grafische rekenmachine de grafiek van `f(x) = sin(x)` en de bijbehorende hellingsgrafiek. Ga na, dat die hellingsgrafiek samenvalt met de grafiek van `y = cos(x)`.
-
Teken zelf (of in GeoGebra) de grafiek van `g(x) = cos(x)`.
- Teken in de grafiek de raaklijn voor `x = 0` en ga na dat de bijbehorende hellingswaarde inderdaad ongeveer 1 is.
- Voor welke waarden van `x` is de helling nog meer 1? En waar is hij `-1`?
- Voor welke waarden van `x` is de helling 0?
- Teken met je grafische rekenmachine de grafiek van `f(x) = sin(x)` en de bijbehorende hellingsgrafiek. Ga na, dat die hellingsgrafiek samenvalt met de grafiek van `y = cos(x)`.
-
Je weet nu hoe je de functie `f(x) = sin(x)` moet differentiëren. Daarnaast ken je alle basisregels voor het differentiëren.
Differentieer nu de volgende functies.
-
`f_1(x) = sin(x) + 2`
-
`f_2(x) = sin(x + 2)`
-
`f_3(x) = 2 sin(x)`
-
`f_4(x) = sin(2x)`
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Differentieerregels > Afgeleide sinusoïde > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Differentieerregels > Afgeleide sinusoïde > Theorie
Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.
Opgaven
-
In Voorbeeld 1 zie je hoe je de afgeleide van een sinusoïde bepaalt.
Differentieer nu zelf de volgende functies.
- `f(x) = 4 sin(2x)`
- `f(x) = 100 + 10 sin(0,5(x - 5))`
- `f(x) = 20 - 15 cos((pi)/(6)(x + 1))`
- `H(t) = 8 sin((2pi)/(15)t) + 4`
-
Gegeven is de functie `f` door `f(x) = 20 + 6 sin((pi)/(6)(x - 2))`.
-
Bepaal van deze functie de afgeleide.
-
Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x = 4`.
-
In welke punten van de grafiek van `f` is de richtingscoëfficiënt van de raaklijn zo groot mogelijk? Hoe groot is die richtingscoëfficiënt?
-
Voorbeeld 2 gaat over het longvolume van een mens bij het in- en uitademen. Ga weer uit van een maximaal longvolume op `t = 0`.
-
Leg uit hoe je aan de formule voor `L` komt. Gebruik de begrippen periode, amplitude, evenwichtsstand.
-
Hoeveel bedraagt zijn longvolume op `t = 1`?
-
Hoeveel bedraagt de snelheid waarmee het longvolume verandert op `t = 1`? Gaat het dan om inademen of uitademen?
-
Op welke tijdstippen is de snelheid van de uitstromende lucht maximaal?
-
Differentieer de volgende functies.
- `f(x) = 2 sin(x) + cos(2x) + 3`
- `f(x) = sin^2(x)`
- `f(x) = cos^2(x) + 3 cos(x)`
- `f(x) = cos^2(3x)`
- `f(x) = (sin(x))/(cos(x))`
-
Bekijk Voorbeeld 3. Het gaat daar om een familie van functies van de vorm `f(x) = sin^2(x) - p sin(x)` op `[0,2pi]`.
- Neem `p = -1`. Om welke functie `f` gaat het nu? Bereken van deze functie alle extremen.
- Bij elke waarde van `p` heeft de grafiek van `f` een top in `A(1/2 pi,f(1/2 pi))` en een top in `B(1 1/2 pi,f(1 1/2 pi))`. Toon dit aan.
- Er zijn twee waarden van `p` waarvoor het punt `A` tweemaal zover van de `x`-as ligt als het punt `B`. Bereken die waarden van `p`.
Verwerken
- Differentieer de volgende functies.
- `f(x) = 3 sin(2x)`
- `g(x) = 16 - 20 cos((2pi)/(30)(x - 5))`
- `H(t) = sin^2(440pi t)`
- `y(x) = sqrt(16 + sin^2(x))`
- `A(r) = 1/(sin(2r))`
- `W(p) = 2 sin(p) cos(2p)`
-
Bekijk de grafiek van de functie `f` met `f(x) = 3 cos(2x) + 1` op `[0,2pi]`.
- Bereken algebra´sch de uiterste waarden van `f`.
- Los algebraïsch op: `f(x) < 2,5` .
- De lijn `y = 2,5` snijdt de grafiek van `f` in vier punten. Bereken de hellingswaarden in die punten.
-
In een bepaald gebied waar eb en vloed heerst wordt de waterhoogte `H` (in m t.o.v. NAP) op tijdstip `t` (in uren) beschreven door `H(t) = 2 cos((2pi)/(12,25)(t - 3)) + 1`.
Hierin is `t = 0` op 0:00 uur van een bepaalde dag.
- Bereken de waterhoogte om 0:00 uur.
- Bereken met behulp van differentiŰren de tijdstippen van hoogwater die dag. Waarom is hierbij differentiëren eigenlijk niet nodig?
- Bereken H'(4). Welke betekenis heeft dit getal voor het verloop van de waterhoogte?
- Op welke tijdstippen verandert de waterstand het snelst?
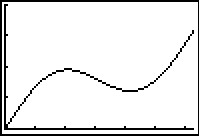 Hier zie je het deel van de grafiek van `f(x) = 0,5x + sin(x)` met `0 <= x <= 2pi`.
Hier zie je het deel van de grafiek van `f(x) = 0,5x + sin(x)` met `0 <= x <= 2pi`.
- Bereken met behulp van differentiëren de twee extremen van `f`.
- Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x = 0`.
- Bereken het punt op de grafiek van `f` waarin de raaklijn het kleinste hellingsgetal heeft en bereken dit hellingsgetal.
-
Bekijk de grafiek van de functie `f` met `f(x) = sin(x^2)`.
Hoeveel extremen heeft deze functie op het interval `[2pi, 3pi]`?
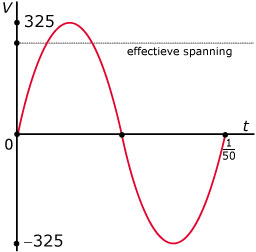 Het vermogen `P` van door energiemaatschappijen geleverde wisselstroom is recht evenredig met het kwadraat van de spanning `V` (in Volt).
Men levert wisselstroom met een effectieve spanning van 230 V, een frequentie van 50 Herz (dat is 50 periodes per seconde) en een amplitudo van ongeveer 325 V.
De spanning `V` als functie van de tijd `t` is een zuivere sinuoïde.
Het vermogen `P` van door energiemaatschappijen geleverde wisselstroom is recht evenredig met het kwadraat van de spanning `V` (in Volt).
Men levert wisselstroom met een effectieve spanning van 230 V, een frequentie van 50 Herz (dat is 50 periodes per seconde) en een amplitudo van ongeveer 325 V.
De spanning `V` als functie van de tijd `t` is een zuivere sinuoïde.
- Stel een formule op voor `V(t)` uitgaande van `V(0)=0`.
- Voor het vermogen `P` geldt: `P(t) = sin^2(100pi t)`. Welke waarde heeft de evenredigheidsconstante in dit geval?
- Bereken algebraïsch de toppen en de nulpunten van `P`.
- De grafiek van `P` is een zuivere sinusoïde. Geef een formule voor die sinusoïde.
Testen
- Differentieer de volgende functies.
- `f(x) = 2 cos(3x)`
- `u(t) = 1,5 sin(220pi (t - 1))`
- `g(x) = x^2 cos(x)`
- `y(t) = 5 cos(0,5pi t - pi) + 0,15t + 2`
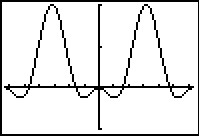 Je ziet hier de grafiek van de functie `f(x) = cos^2(x) - cos(x)` op `[-2pi, 2pi]`.
Je ziet hier de grafiek van de functie `f(x) = cos^2(x) - cos(x)` op `[-2pi, 2pi]`.
- Bereken met behulp van de afgeleide de extremen van `f`.
- Het punt `(1/2 pi,0)` ligt op de grafiek van `f`. Laat zien dat dit inderdaad het geval is. Stel een vergelijking op van de raaklijn aan de grafiek van `f` in dat punt.
-
Het tijdstip van de dagelijkse zonsopkomst verandert in loop van het jaar.
In een bepaald jaar was het vroegste tijdstip van zonsopkomst 4:20 uur op 21 juni en het laatste tijdstip van zonsopkomst 8:50 op 21 december.
Noem het tijdstip van zonsopkomst `Z` en de dag in het jaar `t` met `t = 0` op 1 januari (om 0:00 uur).
- Stel een formule op voor `Z(t)` voor dat jaar.
- Bereken met behulp van de afgeleide de dagen waarop het tijdstip van zonsopkomst het snelst veranderde dat jaar.

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Differentieerregels > Afgeleide sinusoïde > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Differentieerregels > Afgeleide sinusoïde > Inleiding![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Differentieerregels > Afgeleide sinusoïde > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Differentieerregels > Afgeleide sinusoïde > Uitleg![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Differentieerregels > Afgeleide sinusoïde > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Differentieerregels > Afgeleide sinusoïde > Theorie Het vermogen `P` van door energiemaatschappijen geleverde wisselstroom is recht evenredig met het kwadraat van de spanning `V` (in Volt).
Men levert wisselstroom met een effectieve spanning van 230 V, een frequentie van 50 Herz (dat is 50 periodes per seconde) en een amplitudo van ongeveer 325 V.
De spanning `V` als functie van de tijd `t` is een zuivere sinuoïde.
Het vermogen `P` van door energiemaatschappijen geleverde wisselstroom is recht evenredig met het kwadraat van de spanning `V` (in Volt).
Men levert wisselstroom met een effectieve spanning van 230 V, een frequentie van 50 Herz (dat is 50 periodes per seconde) en een amplitudo van ongeveer 325 V.
De spanning `V` als functie van de tijd `t` is een zuivere sinuoïde.