
Totaalbeeld
Samenvatten
Je hebt nu het onderwerp Afgeleide functies doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!
Begrippenlijst:
21: definitie afgeleide — limiet — vergelijking raaklijn
22: differentieerregels — machtsregel voor gehele positieve n — somregel — constante-regel
23: extremen — tekenschema afgeleide
24: buigpunt — tweede afgeleide — buigraaklijn
Activiteitenlijst:
21: afgeleiden bepalen — vergelijking van een raaklijn opstellen
22: afgeleiden bepalen m.b.v. differentieerregels
23: extremen berekenen m.b.v. de afgeleide
24: buigpunten berekenen m.b.v. de tweede afgeleide
Achtergronden
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Afgeleide functies > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Afgeleide functies > Totaalbeeld > Achtergronden
Testen
Opgaven
-
Differentieer de volgende functies:
- `f(x) = 4x^5 - 12x^2 + 60x + 100`
- `E(t) = 1 + t + t^2/2 + t^3/6 + t^4/24`
- `f(x) = (ax + b)^2`
- `GTK(q) = (0,5q^3 + 20q^2 + 60q)/q`
-
Bekijk de grafiek van `f(x) = 2x^3 - x^4` op het interval `[-1,5;2,5]`.
-
De grafiek heeft twee punten waarin de raaklijn horizontaal loopt.
Toon met behulp van differentiëren aan, dat er toch maar één extreme waarde is.
- De grafiek van `f` heeft behalve `(0,0)` nog een buigpunt. Bereken de coördinaten van dat punt.
- Stel de raaklijn op aan de grafiek in het bij b bedoelde buigpunt.
-
Gegeven zijn de functie `f` met `f(x) = 0,5x^3 - 2x`.
- Bereken de extremen van deze functie met behulp van differentiëren.
- Laat zien dat `(0,0)` het buigpunt is van de grafiek van `f`.
-
Stel een vergelijking op van de raaklijn aan de grafiek van `f` in het buigpunt.
-
Een fabriek produceert opvouwbare autopeds voor volwassenen als vervoermiddel in grotere bedrijfshallen. Het bedrijf heeft als enige producent een monopoliepositie. Daarom hangt hun afzet `q` (in duizendtallen) uitsluitend af van de prijs `p` in euro: `q = 12 - 0,1p`. De kosten voor de productie van deze autopeds zijn gegeven door een door de bedrijfswiskundige opgesteld model: `TK = 1,5q^3 - 22,5q^2 + 120q`. Hierin is `TK` gegeven in duizendtallen euro.
- Toon aan dat geldt: `p = 120 - 10q`. Welke waarden kan `q` aannemen?
- Stel een formule op voor de opbrengst `TO` als functie van `q`.
- Stel een formule op voor de winst `TW` als functie van de afzet `q`.
- Bepaal met behulp van differentiëren de prijs van één autoped bij maximale winst.
-
Geef een formule voor de gemiddelde totale kosten `GTK` als functie van `q`.
Bepaal met behulp van differentiëren bij welke afzet `GTK` minimaal is.
-
Gegeven is voor elke reële waarde van `p` de functie `f(x) = x^4 - 4x^3 + px^2`.
Voor welke waarden van `p` heeft de grafiek van `f` precies één minimum?
-
Gegeven zijn de functies: `f(x) = (x^2 - 4)(2x + 1)` en `g(x) = x^2 - 4`.
-
Bepaal algebraïsch de nulpunten en de toppen van de grafiek van `f`.
-
Los op: `f(x) > g(x)`.
-
Gegeven is de functie `f` door `f(x) = x(6 + x)(10 - x)`.
-
Bereken algebraïsch de nulpunten en de toppen van de grafiek van `f`.
-
Voor welke waarden van `p` heeft de lijn `y=p` precies drie punten met de grafiek van `f` gemeen?
-
De raaklijn aan de grafiek van `f` in de oorsprong van het assenstelsel snijdt de grafiek in nog een ander punt.
Bereken algebraïsch de coördinaten van dat punt.
Toepassen
-
Een bedrijf maakt plastic bakjes: bodem en zijvlakken van deze bakjes zijn rechthoeken; de breedte van de bakjes is tweemaal zo groot als de hoogte. Om de bakjes te verstevigen wordt een gebogen metaaldraad met een lengte van 120`cm` aangebracht zoals in de tekeningen is aangegeven.
- Bereken de maximale inhoud die deze bakjes kunnen krijgen.
-
Als het goed is blijkt bij a dat de lengte van het bakje viermaal zo groot is als de hoogte.
Toon aan dat bij elke draadlengte een maximale inhoud ontstaat als de breedte tweemaal de hoogte en de lengte viermaal de hoogte is.
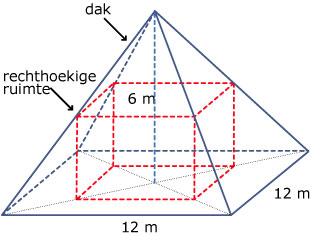 Onder een piramidevormig dak wil je een rechthoekige ruimte bouwen met een zo groot mogelijke inhoud. In de figuur zie je hoe dit er uit komt te zien. Het grondvlak van de ruimte is een vierkant.
Onder een piramidevormig dak wil je een rechthoekige ruimte bouwen met een zo groot mogelijke inhoud. In de figuur zie je hoe dit er uit komt te zien. Het grondvlak van de ruimte is een vierkant.
Welke afmetingen krijgt deze ruimte?
-
Kogelbaan
De kogelbaan is een model voor de baan die een in vacuum (om luchtweerstand te kunnen verwaarlozen) onder een bepaalde hoek en met een bepaalde snelheid afgeschoten massapunt aflegt. Lees hierover
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Afgeleide functies > Totaalbeeld > Toepassen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Afgeleide functies > Totaalbeeld > Toepassen
De kogelbaan blijkt een parabool te worden.
-
Leid zelf de vergelijking van de baan van deze parabool af.
-
Druk het punt waar de kogel weer op de grond komt uit in `v_0`, `alpha` en `g`.
-
Bij welk waarde voor `alpha` komt de kogel zo ver mogelijk? Druk de hoogte die de kogel dan haalt uit in `v_0` en `g`.
Examenopgaven
Gespiegelde afgeleide
In deze opgave onderzoeken we een functie `f`, waarvan de afgeleide functie bestaat voor iedere waarde van `x`. De functie `f` wordt door twee verschillende formules bepaald: een formule voor `x <= 3` en een formule voor `x >= 3`.
Voor `x=3` leveren beide formules dezelfde functiewaarde.
De formule voor `x <= 3` is gegeven. De formule voor `x <= 3` luidt:
`f(x) = -1/2x^2 + 2x + 1`
De formule voor `x >= 3` kun je bepalen als je gebruik maakt van het volgende extra gegeven:
De grafiek van de afgeleide functie `f'` is symmetrisch ten opzichte van de verticale lijn `x=3`.
-
Teken de grafiek van de afgeleide functie `f` en stel een formule op voor de afgeleide `f'` voor `x >= 3`.
-
Een formule voor de functie `f` voor `x >= 3` is van de vorm `f(x) = ax^2 + bx + c`.
Bereken `a`, `b` en `c`.
-
Bereken de extreme waarden van `f`.
-
Teken de grafiek van `f` voor `-1 <= x <= 7`.
(bron: voorbeeldexamen wiskunde B1 havo 2000)
Tennis
Bij sporten als volleybal en tennis is de service erg belangrijk, dat wil zeggen de manier waarop de bal in het spel gebracht wordt. We bekijken hier de service bij tennis. De speler staat bij het serveren 12 meter van het net. Het net is 1 meter hoog. We nemen aan dat de speler de bal raakt op een hoogte van 2,5 meter boven de grond en ter vereenvoudiging gaan we er van uit dat de speler de bal precies in de lengterichting van het veld slaat. In de eerste figuur zie je een mogelijke baan van de bal.
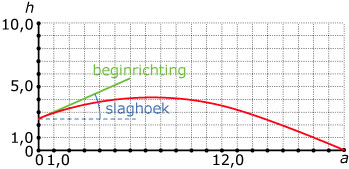
De hoogte van de onderkant van de bal in meter ten opzichte van de grond noemen we `h`. De horizontale afstand in meter noemen we `a`. Het verband tussen `h` en `a` hangt af van de snelheid waarmee de bal geslagen wordt en van de beginrichting. Deze beginrichting wordt bepaald door de slaghoek. Dit is de hoek waaronder de bal geslagen wordt. Zie eerste figuur.
-
Neem aan dat de bal onder een hoek van 15° geslagen wordt met een snelheid van `v` m/s.
Bij deze hoek geldt bij benadering het volgende verband tussen `a` en `h`:
`5,36h = (-5,36)/(v^2) a^2 + 0,27a + 2,50`
Een speler slaat de bal met een snelheid van 17 m/s.
Bereken met behulp van differentiëren de grootste hoogte boven de grond die deze bal bereikt.
In deze vereenvoudigde situatie spreken we van een geldige service als:
- de speler die serveert 12 meter van het net staat;
- de bal precies in de lengterichting van het veld geslagen wordt;
- de bal over het net gaat zonder dit te raken;
- de bal neerkomt op een afstand van ten hoogste 7 meter voorbij het net.
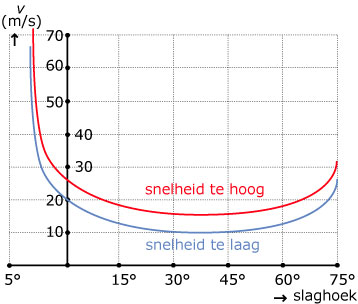 In een artikel over dit onderwerp stond deze grafiek. Daarin is weergegeven bij welke combinaties van slaghoek en snelheid een geldige service verkregenwordt. Een speler die de bal slaat onder een hoek van 30° moet volgens deze grafiek de bal slaan met een snelheid van ongeveer 11 tot 13 m/s. Slaat hij te zacht dan komt de bal niet over het net. Slaat hij te hard dan komt de bal te ver voorbij het net op de grond. Een profspeler slaat bij een geldige service de bal met een snelheid van 150 km/h.
In een artikel over dit onderwerp stond deze grafiek. Daarin is weergegeven bij welke combinaties van slaghoek en snelheid een geldige service verkregenwordt. Een speler die de bal slaat onder een hoek van 30° moet volgens deze grafiek de bal slaan met een snelheid van ongeveer 11 tot 13 m/s. Slaat hij te zacht dan komt de bal niet over het net. Slaat hij te hard dan komt de bal te ver voorbij het net op de grond. Een profspeler slaat bij een geldige service de bal met een snelheid van 150 km/h.
-
Bepaal met behulp van de grafiek de beginrichting van een mogelijke baan van deze bal.
Neem nu aan dat de bal onder een hoek van 10° geslagen wordt. Bij deze hoek geldt bij benadering de volgende formule voor het verband tussen `a` en `h`:
`5,16h = (-5,36)/(v^2) a^2 + 0,18a + 2,50`
Voor een geldige service moet de bal over het net gaan zonder dit te raken. De snelheid is te laag als in bovenstaande formule bij afstand `a=12` de hoogte `h <= 1` is. Volgens de grafiek is een snelheid van 16 m/s of minder te laag voor een geldige service. Echter, met behulp van een berekening is na te gaan dat de figuur hier erg onnauwkeurig is getekend.
-
Welke snelheden (in m/s) zijn volgens de formule te laag voor een geldige service?
Geef je antwoord in ten minste één decimaal nauwkeurig.
Voor een geldige service moet de bal bovendien ten hoogste 7 meter voorbij het net de grond raken. Uit deze eis volgt ook een voorwaarde voor `v`.
-
Welke getallen moet je in de bovenstaande formule invullen om deze voorwaarde te krijgen? Licht je antwoord toe.
(bron: examen wiskunde A vwo 2000, eerste tijdvak)

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Afgeleide functies > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Afgeleide functies > Totaalbeeld > Achtergronden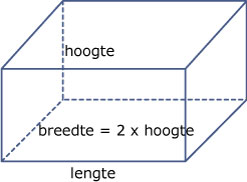

 Onder een piramidevormig dak wil je een rechthoekige ruimte bouwen met een zo groot mogelijke inhoud. In de figuur zie je hoe dit er uit komt te zien. Het grondvlak van de ruimte is een vierkant.
Onder een piramidevormig dak wil je een rechthoekige ruimte bouwen met een zo groot mogelijke inhoud. In de figuur zie je hoe dit er uit komt te zien. Het grondvlak van de ruimte is een vierkant.![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Afgeleide functies > Totaalbeeld > Toepassen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Afgeleide functies > Totaalbeeld > Toepassen
 In een artikel over dit onderwerp stond deze grafiek. Daarin is weergegeven bij welke combinaties van slaghoek en snelheid een geldige service verkregenwordt. Een speler die de bal slaat onder een hoek van 30° moet volgens deze grafiek de bal slaan met een snelheid van ongeveer 11 tot 13 m/s. Slaat hij te zacht dan komt de bal niet over het net. Slaat hij te hard dan komt de bal te ver voorbij het net op de grond. Een profspeler slaat bij een geldige service de bal met een snelheid van 150 km/h.
In een artikel over dit onderwerp stond deze grafiek. Daarin is weergegeven bij welke combinaties van slaghoek en snelheid een geldige service verkregenwordt. Een speler die de bal slaat onder een hoek van 30° moet volgens deze grafiek de bal slaan met een snelheid van ongeveer 11 tot 13 m/s. Slaat hij te zacht dan komt de bal niet over het net. Slaat hij te hard dan komt de bal te ver voorbij het net op de grond. Een profspeler slaat bij een geldige service de bal met een snelheid van 150 km/h.