Totaalbeeld

Antwoorden bij de opgaven

    1. `f'(x) = 20x^4 - 24x + 60`
    2. `E'(t) = 1 + t + 1/2 t^2 + 1/6 t^3`
    3. `f(x) = a^2x^2 + 2abx + b^2` geeft `f'(x) = 2a^2x + 2ab`
    4. `GTK(q) = 0,5q^2 - 20q + 60` geeft `(text(d)GTK)/(text(d)q) = q - 20`
    1. `f'(x) = 6x^2 - 4x^3 = 0` geeft `x=0 vv x=1,5`.
      Aan de grafiek zie je dat er in `(0,0)` wel een horizontale raaklijn maar geen extreme waarde is. De enige extreme waarde is bij `x=1,5`.
    2. `f''(x) = 12x - 12x^2 = 0` geeft `x=0 vv x = 1`. Dus `(1,1)`.
    3. `f'(1) = 2` en dus is de buigraaklijn `y = 2x - 1`.
    1. `f'(x) = 1,5x^2 - 2 = 0` geeft `x = +-sqrt(4/3)`. Max.`f(-sqrt(4/3)) = 1 1/3 sqrt(4/3)` en min.`f(sqrt(4/3)) = -1 1/3 sqrt(4/3)`.
    2. `f''(x) = 3x = 0` geeft `x = 0`. Buigpunt: `(0,0)`.
    3. `f('0) = -2` dus raaklijn `y = -2x`.
    1. Gegeven vergelijking herschrijven.
      `0 <= q <= 12`
    2. `TO = pq = 120q - 10q^2`
    3. `TW = TO - TK = -1,5q^3 + 12,5q^2`
    4. `TW'(q) = -4,5q^2 + 25q = 0` geeft `q=0 vv q = 50/9`.
      `TW` is maximaal bij `q = 50/9` en dan is `p ~~ 64,44` euro.
    5. `GTK = TK/q = 1,5q^2 - 22,5q + 120` en `GTK'(q) = 3q - 22,5 = 0` als `q = 7,5`.
      Dus bij een afzet van 7500 stuks.
  5. `f'(x) = 4x^3 - 12x^2 + 2px = 0` geeft `x=0 vv x = (6 +- sqrt(36 - 8p))/4`.
    Er is maar één nulwaarde als `36 - 8p < 0`, dus als `p > 4,5`.
    1. Nulpunten: `f(x)=0` geeft `x=-1/2 vv x=+-2`, dus `(-1/2,0)`, `(-2,0)` en `(2,0)`.
      Extremen: `f'(x) = 6x^2 + 2x - 8 = 0` geeft `x=-1 1/3 vv x=1`; max.`f(-1 1/3) = 3 19/27` en min.`f(1)=-9`.
    2. `f(x) = g(x)` geeft `x=0 vv x=+-2`.
      Oplossing: `-2 < x < 0 vv x > 2`.
    1. `f(x) = 0` geeft `x=0 vv x=-6 vv x=10` dus nulpunten `(0,0)`, `(-6,0)` en `(10,0)`.
      `f(x) = 60x + 4x^2 - x^3` geeft `f'(x) = 60 + 8x - 3x^2`
      `f'(x) = 0` als `x = (-8 +- sqrt(784))/(-6)` en dit geeft `x=6 vv x = -10/3`.
      Toppen: `(6,288)` en `(-10/3,-3200/3)`.
    2. `-3200/3 < p < 288`
    3. `f(0) = 0` en `f'(0) = 60`, dus de raaklijn is `y=60x`.
      `f(x) = 60x` geeft `4x^2 - x^3 = 0` en dus `x=0 vv x=4`.
      Het gevraagde punt is `(4,240)`.
    1. Lengte = `l`, breedte = `2h` en hoogte = `h`.
      `l + 8h = 120` en `I = l * 2h^2` geeft `I = 2h^2(120 - 8h) = 240h^2 - 16h^3`.
      `I'(x) = 480h - 48h^2 = 0` geeft `h=0 vv h=10`, alleen `h=10` levert een maximum op.
      `h=10` betekent `b=20` en `l=40`, dus `I=8000` cm3.
    2. Zelfde procedure als bij a, maar nu met `l + 8h = p` geeft: `h = 1/12 p`, `b = 1/6 p` en `l = 1/3 p`. Inderdaad is dan `b=2h` en `l=4h`.
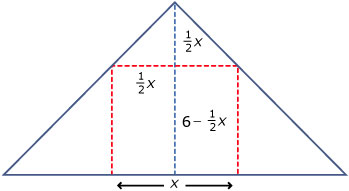  9. Neem voor het grondvlak van de rechthoekige ruimte een vierkant met zijde `x`. Met behulp van gelijkvormigheid kun je dan afleiden dat de hoogte ervan gelijk is aan `h = 6 - 1/2 x`. De inhoud ervan is dan `I = x^2(6 - 1/2 x) = 6x^2 - 1/2 x^3`.
    Met behulp van differentiëren vind je een maximale inhoud als `x=8` en dus `h=2`. De bedoelde afmetingen zijn dus `6 xx 6 xx 2` m.
    1. Zie website.
    2. `x = (2v_0)/g * sin(alpha)cos(alpha)`
    3. `x` is maximaal als `sin(alpha)cos(alpha)` zo groot mogelijk is.
      Maak hiervan een grafiek (`alpha` in graden) voor `0 <= alpha <= 90`. Bij 45° vind je het maximum.
    4. De bijbehorende grootste hoogte is `(v_0)/(4g)`.
    1. Voor `x <= 3` is `f'(x) = -x + 2`, dus voor `x >= 3` is de grafiek van `f'` een lijn met richtingscoëfficiënt 1 die door het punt `(3,-1)` gaat. De formule voor `f'` als `x >= 3` wordt daarom `f'(x) = x - 4`.
    2. Voor `x >= 3` geldt `f'(x) = 2ax + b = x - 4`, dus `a = 0,5` en `b = -4`.
      Dit betekent voor `x >= 3`: `f(x) = 0,5x^2 - 4x + c` en dus `f(3) = -7,5 + c`.
      Omdat voor `x <= 3` geldt `f(3) = 2,5` moet `-7,5 + c = 2,5` en dus `c = 10`.
      Voor `x >= 3` wordt de formule daarom `f(x) = 0,5x^2 - 4x + 10`.
    3. Voor `x <= 3` geldt `f'(x) = -x + 2 = 0` als `x = 2` en is er een maximum `f(2)=3`.
      Voor `x >= 3` geldt `f'(x) = x - 4 = 0` als `x = 4` en is er een minimum `f(4)=2`.
    4. Maak de tekening, je hebt nu beide formules.
    1. als `v = 17` dan `h = –0,0185a^2 + 0,27a + 2,50`.
      `h'(a) = –0,037a + 0,27 = 0` geeft `a ~~ 7,3`.
      Daarbij hoort een maximale hoogte van `h ~~ 3,5` m.
    2. 150 km/u komt overeen met 41,67 m/s.
      Volgens de grafiek hoort daar een hoek bij van ongeveer –5°.
    3. Bij de netsituatie: als `a = 12` dan `h = 1`.
      Dit geeft: `-(5,16)/(v^2) * 12^2 + 0,18 * 12 + 2,50 = 1` en dus `(743,04)/(v^2) = 3,66` en `v ~~ 14,25`. Conclusie: `v <= 14,2` (m/s) of `v < 14,3` (m/s).
    4. 7 meter voorbij het net betekent `a = 19` en de grond raken betekent `h = 0`.