
Buigpunten

Inleiding
Zodra de helling van de grafiek overgaat van toenemende stijging (of daling) naar afnemende
stijging (of daling), of omgekeerd, spreek je van een buigpunt.
In zo'n buigpunt heeft de helling een (locaal) maximum of minimum.
Je vindt buigpunten dus door naar de extremen van de afgeleide te zoeken.
Je leert nu:
- buigpunten berekenen met behulp van de tweede afgeleide van een functie;
- het berekenen van buigpunten toepassen in praktijksituaties;
- buigpunten berekenen bij families van functies.
Je kunt al:
- differentiëren met de machtsregel, de somregel en de constante-regel;
- werken met de diverse soorten functies;
- extremen bepalen met behulp van differentiëren.
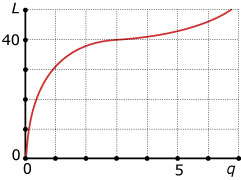
Verkennen
De afstand `a` (in meter) voor van een bewegend voorwerp ten opzichte van zijn startpunt
(bij `t = 0`) wordt gegeven door `a(t) = t^3 - 6t^2 + 36t`.
Het voorwerp heeft op `t = 0` al een flinke beginsnelheid.
Vervolgens remt het af en na omstreeks `6` seconden gaat het weer versnellen.
> Hoe zie je dat aan de grafiek?
> Door differentiëren kun je een formule opstellen voor de snelheid van dit voorwerp. Welke formule is dat?
> Hoe kun je een formule opstellen voor de verandering van die snelheid, de versnelling?
> Het tijdstip waarop het voorwerp van vertragen overgaat in versnellen kun je exact berekenen. Laat zien hoe.

Uitleg
Je ziet hier de grafiek van de functie
`f(x) = x^3 - 20x^2 + 150x + 100`.
De functiewaarden stijgen voortdurend:
- ongeveer tot `x=7` is er afnemende stijging;
- ongeveer vanaf `x=7` is er toenemende stijging;
- ongeveer bij `x=7` zit een buigpunt.
Om dit buigpunt te schatten, kijk je naar het verloop van de helling van de grafiek.
Die helling neemt eerst af en daarna weer toe, heeft een minimale waarde bij het buigpunt.
Om het buigpunt exact te berekenen zoek je een minimum van de afgeleide.
De afgeleide is: `f'(x) = 3x^2 - 40x + 150`.
Een minimum van deze functie kun je vinden door differentiëren. Je bepaalt dan de afgeleide
van `f'`, de afgeleide van de afgeleide dus. Je spreekt dan van de tweede afgeleide die je aangeeft met `f"`.
Hier is `f"(x) = 6x - 40`.
Deze tweede afgeleide verandert van teken als `6x - 40 = 0` dus als `x = 40/6 ~~ 6,67`.
Het buigpunt zit daarom bij `x ~~ 6,67`. Om het volledig te berekenen moet je dit nog invullen in het functievoorschrift van `f`.
Het buigpunt is ongeveer `(6,67; 507,41)`.
‡
Opgaven
-
In de Uitleg zie wat een buigpunt van een grafiek is en hoe je dit kunt berekenen.
- Voer de berekening zelf uit en bepaal het buigpunt exact.
- Is in dit buigpunt ook de richtingscoëfficiënt van de raaklijn `0`? Licht je antwoord toe.
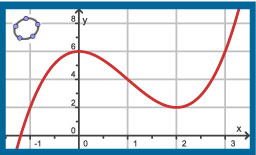 Dit is een deel van de grafiek van `f(x) = x^3 - 3x^2 + 6`.
Dit is een deel van de grafiek van `f(x) = x^3 - 3x^2 + 6`.
-
Zolang `x < 1` wordt de helling van de grafiek steeds kleiner.
Wat betekent dit voor de afgeleide van de hellingsfunctie `f'(x)`?
- Die is dan dalend.
- Die is dan negatief.
- Die heeft dan een minimum.
-
Het punt `(1,4)` van de grafiek van `f` noem je een buigpunt omdat de helling daar overgaat van dalend in stijgend.
Wat weet je van de afgeleide in dit buigpunt?
En van de afgeleide van de afgeleide?
- De afgeleide is minimaal, de afgeleide van de afgeleide 0.
- De afgeleide is minimaal, de afgeleide van de afgeleide ook.
- De afgeleide is negatief, de afgeleide van de afgeleide 0.
- De afgeleide is 0, de afgeleide van de afgeleide minimaal.
-
De afgeleide van de afgeleide noem je wel de tweede afgeleide van de gegeven functie.
Met behulp van de tweede afgeleide kun je het buigpunt algebraïsch berekenen.
Laat zien hoe dat gaat.
Theorie
Bij toenemende stijging (daling) of afnemende stijging (daling) kijk je naar de veranderingen van de helling:
- Bij toenemende stijging wordt de helling steeds groter: `f'` stijgt. De afgeleide van `f'` is dan positief.
- Bij toenemende daling wordt de helling steeds kleiner (negatiever): `f'` daalt. De afgeleide van `f'` is dan negatief.
- Bij afnemende stijging wordt de helling steeds kleiner: `f'` daalt. De afgeleide van `f'` is dan negatief.
- Bij afnemende daling wordt de helling steeds groter: `f'` stijgt. De afgeleide van `f'` is dan positief.
De afgeleide van `f'` heet de tweede afgeleide van `f`.
De tweede afgeleide noteer je als: `f''` of `(text(d)^2 f)/(text(d)x^2)`.
Het punt waarin de helling overgaat van toenemend naar afnemend (of omgekeerd) heet een buigpunt van de grafiek.
Je vindt die buigpunten door naar de extremen van de afgeleide te zoeken.
Dat doe je met behulp van de tweede afgeleide.
‡
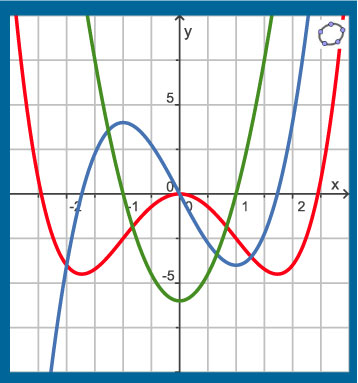
Voorbeeld 1
Je ziet hier de grafieken van de functie
`f(x) = 1/2x^4 - 3x^2`
(rood), zijn afgeleide (blauw) en zijn tweede afgeleide.
Ga na dat:
- op `(:larr,-1:)` de grafiek van `f` een toenemende helling heeft, `f'` stijgend is en `f''(x) > 0`;
- op `(:-1,1:)` de grafiek van `f` een afnemende helling heeft, `f'` dalend is en `f''(x) < 0`;
- op `(:1,rarr:)` de grafiek van `f` een toenemende helling heeft, `f'` stijgend is en `f''(x) > 0`;
Er zijn daarom twee buigpunten, namelijk
`(-1; 7,5)` en `(1; 7,5)`.
‡
Voorbeeld 2
Gegeven is de functie `f(x) = 0,5x^3 - 3x^2 + 2x + 3`.
Onderzoek of de grafiek van deze functie een buigpunt heeft.
Zo ja, bereken de coördinaten ervan.
Antwoord
Eerst de afgeleide bepalen: `f'(x) = 1,5x^2 - 6x +2`.
Vervolgens deze afgeleide nog eens differentiëren: `f''(x) = 3x - 6`.
Deze tweede afgeleide geeft informatie over het stijgen of dalen van de helling. Er is sprake van een buigpunt als de helling overgaat van stijgen in dalen, of omgekeerd. De tweede afgeleide gaat dan over van positief in negatief, of omgekeerd. Dat is vaak het geval voor waarden van x waarin de tweede afgeleide 0 is.
Je lost daarom eerst op: `f''(x) = 3x - 6 = 0`.
Dit geeft `x=2`.
De tweede afgeleide wisselt bij `x=2` van teken, er is een buigpunt met `f(2) = -1`.
Het buigpunt is `(2,-1)`.
‡
Voorbeeld 3
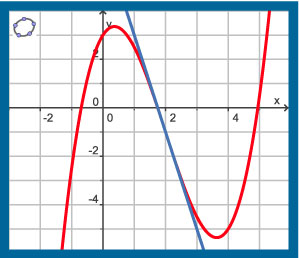
Hier zie je de grafiek van de functie `f(x) = 0,5x^3 - 3x^2 + 2x + 3` uit het vorige voorbeeld.
De getekende lijn is de raaklijn in het buigpunt, kortweg de buigraaklijn.
Stel er een formule voor op.
Antwoord
In voorbeeld 2 zie je dat het buigpunt `(2,-1)` is.
Je vindt er ook de afgeleide en de tweede afgeleide van `f`.
De helling in dat punt is `f'(2) = -4`.
Dus heeft de getekende raaklijn een formule van de vorm
`y = -4x + b`,
waarin je `b` kunt vinden door een punt van de raaklijn (het buigpunt natuurlijk) in te vullen.
Ga na, dat je vindt: `y = -4x + 7`.
‡
Opgaven
-
In Voorbeeld 1 zie je de grafiek van de functie `f(x) = 1/2 x^4 - 3x^2` samen met zijn afgeleide en zijn tweede afgeleide.
In Voorbeeld 2 zie je hoe je de buigpunten van de grafiek van een andere functie algebraïsch berekent.
-
Bereken de buigpunten van `f(x) = 1/2 x^4 - 3x^2` algebraïsch.
-
Laat ook zien dat uit de functievoorschriften van de afgeleide en de tweede afgeleide inderdaad volgt dat de grafiek van `f` op `(:0,1:)` toenemend dalend is.
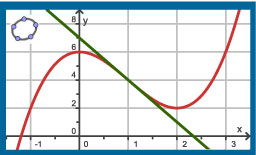 Hier zie je de grafiek van `f(x) = x^3 - 3x^2 + 6` met daarin de buigraaklijn, de raaklijn in het buigpunt, getekend.
Hier zie je de grafiek van `f(x) = x^3 - 3x^2 + 6` met daarin de buigraaklijn, de raaklijn in het buigpunt, getekend.
- Welke coördinaten heeft het buigpunt?
- Welke richtingscoëfficiënt heeft deze raaklijn?
- Stel een vergelijking op van de getekende buigraaklijn.
-
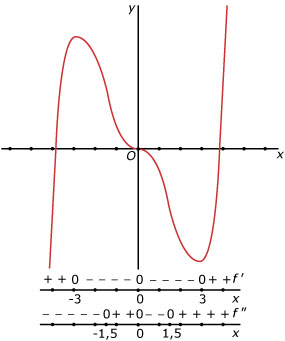
Van een functie zijn de tekenschema’s van `f(x)`, van `f'(x)` en van `f''(x)` gegeven door deze figuren.
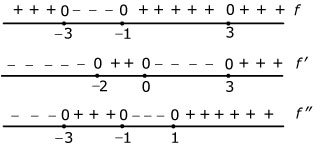
- Hoeveel buigpunten boven de `x`-as heeft de grafiek van `f`?
- Schets een mogelijke grafiek van `f`.
-
Vaak is de opbrengst `TO` bij de productie van een bepaald artikel afhankelijk van de ingezette arbeidstijd `a` (in uren per dag). Een dergelijk verband kan worden beschreven door de functie `TO(a) = -1/3 a^3 + 8a^2`.
-
Bekijk de grafiek van `TO`.
De opbrengst stijgt in het begin progressief (steeds sterker).
Schat tot hoeveel ingezette arbeidstijd dat ongeveer zo is.
-
Het antwoord op de voorgaande vraag kun je nauwkeurig berekenen met behulp van differentiëren. Laat zien hoe dat gaat.
-
Hoeveel bedraagt de grootste opbrengststijging per uur?
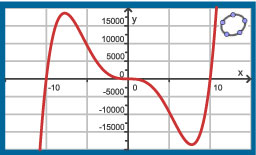 Functies kunnen meerdere buigpunten hebben. Hier zie je de grafiek van de functie `f(x) = x^3(x^2 - 100)`.
Functies kunnen meerdere buigpunten hebben. Hier zie je de grafiek van de functie `f(x) = x^3(x^2 - 100)`.
- Bereken de exacte extremen van deze functie.
- Bereken de exacte buigpunten van deze grafiek.
Verwerken
-
Bepaal met behulp van differentiëren van de volgende functies alle buigpunten.
- `f(x) = 0,5x^3 + 6x^2 - 90`
- `y(x) = 4x^2 - 0,5x^4`
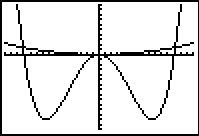 Gegeven zijn de functies `f(x) = x^2` en `g(x) = 0,25x^2(x^2 - 144)`.
Gegeven zijn de functies `f(x) = x^2` en `g(x) = 0,25x^2(x^2 - 144)`.
-
Je ziet hier hoe de grafieken van beide functies er op de grafische rekenmachine uit kunnen zien.
Hoe moet je het venster dan instellen?
- Los op: `f(x) > g(x)`
- Bereken de exacte buigpunten van de grafiek van `g`.
-
De grafiek van `g` heeft twee buigraaklijnen die elkaar snijden op de `y`-as.
Bereken de exacte coördinaten.
-
Een ondernemer maakt een bepaald product waarop hij het monopolie heeft. Voor zijn productiekosten (in honderden euro) geldt de formule `TK = 0,5q^3 - 4q^2 + 11q + 4` waarin `q` de geproduceerde hoeveelheid in honderden kilogram is.
-
De snelheid waarmee de kosten stijgen is eerst afnemend, later toenemend.
Er is een punt in de grafiek waarbij die snelheid van afnemend naar toenemend omslaat.
Bij welke productie zit het omslagpunt? Rond je antwoord af op hele kilogrammen nauwkeurig.
-
De hoeveelheid product die hij aanbiedt aan zijn afnemers heeft invloed op de prijs.
Er geldt: `p = 11 - q` waarin `p` de prijs in honderden euro is.
Ga er van uit dat deze ondernemer zijn totale productie ook verkoopt.
Bij welke productie is zijn winst maximaal? Licht het antwoord toe met behulp van differentiëren.
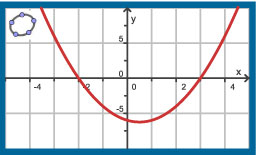 Dit is de grafiek van de afgeleide van een functie.
Dit is de grafiek van de afgeleide van een functie.
- Bij welke waarden van `x` heeft deze functie extremen?
- Bij welke waarden van `x` heeft de grafiek van deze functie een buigpunt?
- Heeft de buigraaklijn een positieve of een negatieve richtingscoëfficiënt?
-
Gegeven is de functie `f(x) = x^4 + ax^2` met een constante `a > 0`.
- Laat zien, dat deze functie voor elke waarde van `a` een minimum heeft.
- Toon aan dat deze functie voor geen enkele `a` een buigpunt heeft.
Testen
-
Onderzoek telkens of de functie met het genoemde functievoorschrift een buigpunt heeft.
Zo ja, bereken de coördinaten van dit buigpunt.
- `f(x) = x^3 - 6x^2 + 12`
- `y = 0,25x^4 - 5x^3`
-
Van een functie `f` is de afgeleide gegeven door `f'(x) = 4x - 0,5x^2`.
- Bereken de `x`-waarde van het buigpunt.
-
Op grond van deze afgeleide kun je een schets maken van de grafiek van de functie als je weet dat de `y`-waarde van het buigpunt 10 is.
Maak een mogelijke schets van de grafiek van`f`?
-
Stel een vergelijking op van de buigraaklijn van de grafiek van `f`.
-
Een verffabriek gebruikt de functie `TK = 0,5q^3 - 3q^2 + 6q` voor de productiekosten voor een bepaald soort verf. Hierin is `q` de hoeveelheid geproduceerde verf in duizenden liters per dag en verder stelt `TK` de kosten in duizenden euro voor.
-
De marginale kosten zijn de meerkosten per liter die ontstaan bij de productie van 1 liter extra.
Bereken de marginale kosten bij een productie van 3000 liter verf per dag.
-
Je kunt de marginale kosten goed benaderen met behulp van de afgeleide: `MK = TK'`.
Bereken ook op deze manier de marginale kosten bij een productie van 3000 liter per dag.
-
De ondernemer produceert het liefst een hoeveelheid waarbij de marginale kosten minimaal zijn.
Bij welke productie in liter per dag is dat het geval? Bereken het antwoord algebraïsch.
 Dit is een deel van de grafiek van `f(x) = x^3 - 3x^2 + 6`.
Dit is een deel van de grafiek van `f(x) = x^3 - 3x^2 + 6`.







 Hier zie je de grafiek van `f(x) = x^3 - 3x^2 + 6` met daarin de buigraaklijn, de raaklijn in het buigpunt, getekend.
Hier zie je de grafiek van `f(x) = x^3 - 3x^2 + 6` met daarin de buigraaklijn, de raaklijn in het buigpunt, getekend.
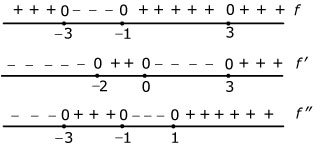
 Functies kunnen meerdere buigpunten hebben. Hier zie je de grafiek van de functie `f(x) = x^3(x^2 - 100)`.
Functies kunnen meerdere buigpunten hebben. Hier zie je de grafiek van de functie `f(x) = x^3(x^2 - 100)`.
 Gegeven zijn de functies `f(x) = x^2` en `g(x) = 0,25x^2(x^2 - 144)`.
Gegeven zijn de functies `f(x) = x^2` en `g(x) = 0,25x^2(x^2 - 144)`.
 Dit is de grafiek van de afgeleide van een functie.
Dit is de grafiek van de afgeleide van een functie.