
Extremen berekenen

Inleiding
Als je een functievoorschrift hebt, kun je met de grafische rekenmachine een bijpassende grafiek tekenen.
Je kunt dan de extreme waarden door de machine laten berekenen.
Nadeel daarvan is dat je vaak niet zeker weet of je alle extremen in beeld hebt.
Verder kan je rekenmachine ze alleen maar benaderen.
Met behulp van de afgeleide van de functie kun je extremen echt berekenen: het zijn de punten van de grafiek waarin
de afgeleide overgaat van positief in negatief of omgekeerd.
Je leert nu:
- extremen berekenen met behulp van de afgeleide van een functie;
- het berekenen van extremen toepassen in praktijksituaties;
- extremen berekenen bij families van functies.
Je kunt al:
- differentiëren met de machtsregel, de somregel en de constante-regel;
- werken met de diverse soorten functies;
- extremen bepalen met behulp van de GR en met behulp van hellingsgrafieken.
Verkennen
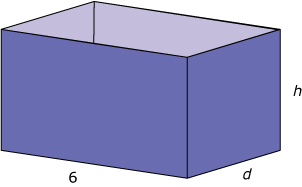
Iemand bouwt in zijn schuur een rechthoekige opbergbak met bodem en zonder deksel.
De breedte van de bak moet 6 dm worden, meer ruimte is er niet.
De inhoud van de bak moet 1 m3 worden.
De diepte en de hoogte van de bak kunnen nog variëren.
Bij welke diepte en welke hoogte wordt de totale oppervlakte van de bak minimaal?
(Dan zijn waarschijnlijk de materiaalkosten het laagst.)
> Probeer dit probleem zelf op te lossen. Denk bijvoorbeeld aan het kiezen van geschikte variabelen.
Over probleemaanpak vind je meer bij de rubriek "Probleemaanpak" op deze site.
Uitleg
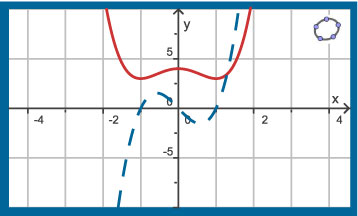
Je ziet hier de grafiek (rood) van de functie `f(x) = x^4 - 2x^2 + 4`.
De andere grafiek is de hellingsgrafiek van `f`, dus de grafiek van de afgeleide `f'`.
Als je goed kijkt zie je dat:
- de grafiek van `f` een minimum heeft als de afgeleide overgaat van negatief naar positief;
- de grafiek van `f` een maximum heeft als de afgeleide overgaat van positief naar negatief.
Voor het berekenen van extremen is het dus van belang om te weten te komen voor welke waarden van `x`
de afgeleide overgaat van positief in negatief en omgekeerd.
Vaak is dat het geval bij de nulwaarden van de afgeleide en daarom begin je met die op te zoeken.
De afgeleide van `f` is: `f'(x) = 4x^3 - 4x`.
Deze afgeleide heeft nulwaarden als `4x^3 - 4x = 0`, dus als
`4x(x^2 - 1) = 0`. Daaruit volgt: `x=0 vv x=-1 vv x=1`.
Aan de grafiek van `f` kun je zien of er bij deze nulwaarden ook echt extremen optreden: de afgeleide moet er
van teken wisselen. Dat geldt hier bij alle drie de nulwaarden, dus er zijn drie extremen:
min.'`f(-1) = 3`, max.`f(0) = 4` en min.`f(1) = 3`.
‡
Opgaven

-
Als de afgeleide van een functie `f` de waarde 0 heeft, heeft de grafiek van `f` voor de bijbehorende waarde van `x` een horizontale raaklijn. Vaak hoort daar een extreme waarde van `f` bij.
- Gegeven is de functie `f(x)=x^3-3x`. Bepaal de afgeleide van `f`.
- Bereken de nulwaarden van de afgeleide.
-
In de grafiek kun je zien welke extremen de functie `f` heeft: welke (locale) maxima en welke (locale) minima.
De bijbehorende `x`-waarden heb je nu ook gevonden. De extremen zelf (de functiewaarden) moet je nog uitrekenen.
Bereken de extremen van `f`.
Theorie
Extremen berekenen gaat bij een functie, waarvan `f(x)` het functievoorschrift is, als volgt:
- bepaal met behulp van differentiëren de afgeleide en los op `f'(x) = 0`, rekening houdend met het domein van de functie;
- bekijk de grafiek van de afgeleide of maak een tekenschema van de afgeleide;
- gaat `f'(x)` voor `x = a` over van negatief in positief (en hoort `a` tot het domein van de functie) dan heeft `f` een (locaal) minimum van `f(a)`;
- gaat `f'(x)` voor `x = b` over van positief in negatief (en hoort `b` tot het domein van de functie) dan heeft `f` een (locaal) maximum van `f(b)`.
Als de afgeleide niet van teken wisselt is er van een extreme waarde geen sprake!
Hieronder zie je het tekenschema van de afgeleide.
‡
Voorbeeld 1
Bereken de extremen van de functie `f(x) = 25x^4 - 800000x - 12345`.
Antwoord
Echt een functie waarvan je de grafiek niet zomaar goed in beeld krijgt met je grafische rekenmachine.
Nu is het werken met de afgeleide erg handig.
Differentiëren levert op: `f'(x) = 100x^3 - 800000`.
De volgende stap is `f'(x) = 100x^3 - 800000 = 0` oplossen.
Dat geeft: `x = root[3](8000) = 20`.
Maak bijvoorbeeld een tekenschema van de afgeleide. Dat doe je door zowel links als rechts van `x = 20` even een getal te kiezen en dit in de afgeleide in te vullen: `f'(0) = -800000` en `f'(25) = 1482500 > 0`.
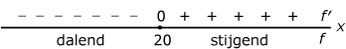
Er is precies één extreme waarde, dat kun je aan het tekenschema van `f'` ook zien:
min.`f(20) = 2.387.655`.
‡

Voorbeeld 2
Iemand bouwt in zijn schuur een rechthoekige opbergbak met bodem en zonder deksel.
De breedte van de bak moet 6 dm worden, meer ruimte is er niet.
De inhoud van de bak moet 1 m3 worden.
De diepte en de hoogte van de bak kunnen nog variëren.
Bij welke diepte en welke hoogte wordt de totale oppervlakte van de bak minimaal?
(Dan zijn waarschijnlijk de materiaalkosten het laagst.)
Antwoord
Noem de diepte `d` en de hoogte `h`, beide in dm.
Vanwege de inhoud van 1 m3 = 1000 dm3, geldt: `1000 = 6 * d * h` en dus `h = 1000/(6d)`.
Voor de totale oppervlakte `A` in m2 geldt: `A = 6d + 12h + 2dh`.
Als je nu de eerder gevonden uitdrukking invult in de oppervlakteformule, vind je `A = 6d + 2000/d + 1000/3`.
Van deze functie van `d` moet je het minimum bepalen. Omdat je een functie van deze vorm nog
niet kunt differentiëren, doe je dat met behulp van de grafische rekenmachine. Ga na dat je
vindt: `d ~~ 18,26`. De bijbehorende waarde voor de hoogte kun je dan ook wel berekenen.
‡
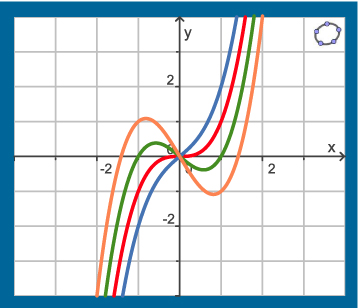
Voorbeeld 3
Gegeven is de familie van functies`f_a(x) = x^3 + ax`.
Voor elke waarde van `a` heb je hier met een andere functie te maken.
Je kunt hier een paar grafieken van deze familie van functies zien door `a` te variëren. Sommige functies `f_a` hebben extremen, andere niet.
De vraag is nu hoe de extremen van `f_a` afhangen van de waarde van `a`.
Antwoord
De afgeleide is `f_a'(x) = 3x^2 + a`.
Deze afgeleide heeft als nulwaarden `x = sqrt(-a/3) vv x = -sqrt(-a/3)`.
Er zijn dus alleen nulwaarden als `a <= 0` omdat de wortels anders geen reële waarden opleveren. De twee mogelijkheden zijn:
-
Als `a = 0`, dan is alleen `x = 0` de nulwaarde. De afgeleide is dan `f_0'(x) = 3x^2` en is dus voor elke waarde van `x` positief of 0.
Er zijn geen extremen, in `(0,0)` heeft de grafiek een horizontale raaklijn.
-
Als `a < 0` dan zijn er twee nulwaarden. De afgeleide is een dalparabool met twee nulpunten. Er is
een maximum voor `x = -sqrt(-a/3)` en een minimum voor `x = sqrt(-a/3)`.
‡
Opgaven
-
Gegeven is de functie `f(x) = 0,1x^3 - 120x`. Soms is een grafiek goed in beeld brengen nog lastig.
Je kunt dan om te bepalen of er sprake is van een extreem en of het een maximum dan wel een minimum is, een tekenschema maken van de afgeleide. Zie Voorbeeld 1.
-
Bepaal de afgeleide van `f`.
-
Bereken de nulwaarden van de afgeleide.
-
Maak een tekenschema van de afgeleide van `f`.
Geef er de plaats van de extremen in aan.
-
Bekijk de grafiek van de functie `f(x) = x^3`.
- Bereken de waarden van `x` waarin `f'(x)=0`.
- Deze functie heeft voor `x=0` een horizontale raaklijn. Heeft de functie ook een extreme waarde voor `x=0`?
- Ja.
- Nee.
- Bekijk de grafiek van de functie `g(x) = |x|`. Wat is er aan de hand in `x=0`?
- De functie en de afgeleide hebben er beide de waarde 0, maar er is geen sprake van een extreme waarde.
- De functie en de afgeleide hebben er beide de waarde 0, en er is een minimum van `f(0)=0`.
- Alleen de functie heeft er de waarde 0 en `f'(0)` is onbekend. Er is geen extreme waarde.
- Alleen de functie heeft er de waarde 0 en `f'(0)` is onbekend. Er is een minimum van `f(0)=0`.
-
Gegeven zijn de functies `f(x) = 100x^2` en `g(x) = x^2 * (x - 10)^2.
- Bereken algebraïsch de snijpunten van beide grafieken.
- Bereken met behulp van differentiŽren de extremen van `g`.
-
Als je het getal 100 in het functievoorschrift van `f` vervangt door een ander getal, gaat de grafiek door het punt waarin `g` een maximum heeft. Door welk getal moet je 100 vervangen? En hoeveel snijpunten hebben beide grafieken dan?
-
Een fabrikant verpakt zijn hagelslag al jaren in doosjes met een vierkante bodem van 8 bij 8 cm . Ze hebben precies de vorm van een balk met een hoogte van 21 cm.
Hij vraag zich nu af of hij de inhoud van het doosje kan vergroten door de afmetingen anders te kiezen, zonder echter meer karton te gebruiken. Het gaat er dus om de inhoud zo groot mogelijk te maken bij een gelijkblijvende oppervlakte. Het grondvlak blijft vierkant. Welke afmetingen moet hij kiezen?
- Hoeveel karton heeft de fabrikant nodig voor zijn huidige doosjes?
- Noem de zijde (in cm) van het grondvlak `x`. Bepaal de hoogte `h` van de doosjes uitgedrukt in `x`.
- Stel een formule op voor de inhoud van de doosjes.
- Voor welke waarde van `x` is de inhoud maximaal? (Maak gebruik van differentiëren.)
- Bepaal de afmetingen van de doosjes met een maximale inhoud in millimeter nauwkeurig.
-
Gegeven is de functie `f(x) = ax^3 - x`, waarin `a` een nog onbekende positieve constante is. Bekijk eventueel eerst even Voorbeeld 3.
- Druk de waarde(n) van `x` waarin de raaklijn aan de grafiek van `f` evenwijdig aan de `x`-as loopt uit in `a`.
- Druk de extremen van `f` uit in `a`.
- Voor welke waarde van `a` is de maximale waarde van `f` gelijk aan 1?
Verwerken
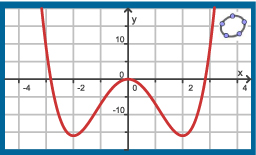 Je ziet hier de grafiek van de functie `f(x) = x^4 - 8x^2`.
Je ziet hier de grafiek van de functie `f(x) = x^4 - 8x^2`.
Bereken met behulp van differentiëren alle extremen van deze functie.
-
Gegeven zijn de functies `f(x) = 4000 - 10x^2` en `g(x) = (x - 10)(x^2 - 400)`.
-
Om de grafieken van beide functies in beeld te krijgen op je grafische rekenmachine moet je de instellingen nogal aanpassen.
Bereken eerst de nulpunten van beide functies.
- Nu weet je welke waarden voor `x` je het beste kunt instellen. Bereken de extremen van beide functies.
- Je kunt nu de grafieken natuurlijk heel mooi in beeld krijgen. Los op: `f(x) >= g(x)`.
 Om een rechthoekig sportveld ligt een sintelbaan, bestaande uit twee rechte stukken en twee halve cirkels. De totale lengte van de sintelbaan is 400 m. De afmetingen van het veld zijn zo gekozen dat de oppervlakte van het sportveld maximaal is. Bereken exact de afmetingen van dit sportveld.
Om een rechthoekig sportveld ligt een sintelbaan, bestaande uit twee rechte stukken en twee halve cirkels. De totale lengte van de sintelbaan is 400 m. De afmetingen van het veld zijn zo gekozen dat de oppervlakte van het sportveld maximaal is. Bereken exact de afmetingen van dit sportveld.
-
Een fabrikant van zelfrijzend bakmeel verkoopt dat voor € 2,25 per kilogram. Voor de kosten `TK` voor productie en opslag geldt:
| `q` (in honderden kg) |
1 |
2 |
3 |
4 |
5 |
6 |
| `TK` (in euro) |
75 |
100 |
125 |
200 |
400 |
800 |
-
Hoeveel stijgt de winst gemiddeld per kilogram als de productie toeneemt van 400 naar 500 kg?
-
Voor de kosten heeft de fabrikant de formule `TK = 10q^3 - 60q^2 + 130q` laten opstellen.
Ga na dat deze formule past bij de gegevens in de tabel.
-
Stel een formule op voor de winst als functie van `q`.
-
Bereken de marginale winst bij een productie van 400 kilo met behulp van `MW(q)=TW'(q)`.
Welke economische betekenis heeft dit getal?
-
Bereken de maximale winst met behulp van de functie `MW`.
-
Gegeven is voor elke waarde van `a` de functie `f(x) = x^4 - ax^2`.
-
Voor welke waarden van `a` is het minimum van deze functie gelijk aan `-1`?
-
De raaklijn aan de grafiek van `f` voor `x=1` gaat door het punt `(0,4)`.
Voor welke waarde van `a` is dit het geval?
- Voor elke positieve waarde van `p` bestaat er een functie van de vorm `f(x) = x^3 - 6px^2 - 16`.
-
Heeft elk van die functies extreme waarden? Licht je antwoord toe.
-
Voor welke waarde van `p` heeft de gegeven functie een uiterste waarde van `-32`?
Is het dan een minimum of een maximum?
Testen
-
Bereken bij deze functies de extremen met behulp van een tekenoverzicht van de afgeleide.
- `f(x) = -x^4 + 2x^3`
- `y = x^2(x - 6)`
-
Gegeven is de functie `f(x) = 4x^5 - 80000x^2 + 2557`.
- Bepaal de extreme waarden van deze functie met behulp van de grafische rekenmachine.
- Bereken de extremen met behulp van differentiŽren.
- Hoeveel oplossingen heeft de vergelijking `f(x)=0`?
 Van een vierkant stuk karton wordt een bakje gemaakt door in de hoeken vierkantjes in te knippen en de randen om te vouwen. Die vierkantjes dienen dan als plakrandjes.
Van een vierkant stuk karton wordt een bakje gemaakt door in de hoeken vierkantjes in te knippen en de randen om te vouwen. Die vierkantjes dienen dan als plakrandjes.
-
Stel dat de zijde van het ingeknipte vierkantje `x` wordt genoemd.
Welke formule kun je dan opstellen voor de inhoud `I` van dit bakje?
-
Welke waarden kan `x` allemaal aannemen?
-
De maximale inhoud van dit bakje kun je berekenen met behulp van de grafische rekenmachine en met behulp van differentiŽren.
Doe dit op beide manieren.
-
Functies van de vorm `f(x) = ax^3 + bx + c` noem je derdegraads functies zolang `a != 0`.
-
Hoe noem je deze functies als `a=0`?
-
Neem verder aan dat `a != 0`.
Sommige van deze functies hebben extreme waarden.
Druk de bijbehorende waarden van `x` uit in `a` en `b`.
-
Voor welke waarden van `a` en `b` zijn er inderdaad extreme waarden?






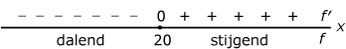

 Je ziet hier de grafiek van de functie `f(x) = x^4 - 8x^2`.
Je ziet hier de grafiek van de functie `f(x) = x^4 - 8x^2`. Om een rechthoekig sportveld ligt een sintelbaan, bestaande uit twee rechte stukken en twee halve cirkels. De totale lengte van de sintelbaan is 400 m. De afmetingen van het veld zijn zo gekozen dat de oppervlakte van het sportveld maximaal is. Bereken exact de afmetingen van dit sportveld.
Om een rechthoekig sportveld ligt een sintelbaan, bestaande uit twee rechte stukken en twee halve cirkels. De totale lengte van de sintelbaan is 400 m. De afmetingen van het veld zijn zo gekozen dat de oppervlakte van het sportveld maximaal is. Bereken exact de afmetingen van dit sportveld. Van een vierkant stuk karton wordt een bakje gemaakt door in de hoeken vierkantjes in te knippen en de randen om te vouwen. Die vierkantjes dienen dan als plakrandjes.
Van een vierkant stuk karton wordt een bakje gemaakt door in de hoeken vierkantjes in te knippen en de randen om te vouwen. Die vierkantjes dienen dan als plakrandjes.