Differentiëren

Inleiding

Je hebt gezien dat bij een functie vaak een afgeleide (functie) is op te stellen. Die afgeleide zegt iets over de veranderingen van de grafiek van de functie. En dus over de helling van die functie.
Het differentiëren is een handige techniek om afgeleiden te vinden.

Je leert nu:

• bij bepaalde soorten functies de afgeleide snel te vinden;
• het begrip differentiëren;
• afgeleiden gebruiken bij het berekenen van hellingwaarden en bij gegeven hellingwaarden de bijpassende x-waarden berekenen.

Je kunt al:

• met behulp van een differentiequotiënt de afgeleide (of hellingsfunctie) van een functie bepalen;
• een hellingsfunctie gebruiken om de vergelijking van een raaklijn aan de grafiek op te stellen.

Verkennen

Je hebt geleerd hoe je de hellingsfunctie (de afgeleide) van `y = f(x)` met behulp van het differentiequotiënt op het interval `[x,x + h]` kunt bepalen.

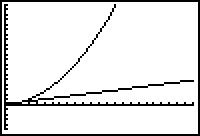
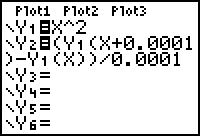
Met je grafische rekenmachine kun je de bijbehorende hellingsgrafiek benaderen door bijvoorbeeld `h = 0,0001` te kiezen.
In de twee rekenmachinevensters zie je hoe dat gaat bij `f(x) = x^2`.

> Ga met je rekenmachine na, dat de gevonden hellingsgrafiek overeen komt met de grafiek van `y = 2x`.
> Voer nu bij Y1 steeds een functie in. Doe dat systematisch, bijvoorbeeld eerst functies van de vorm `f(x) = ax^2 + b`. En dan bijvoorbeeld van de vorm `f(x) = ax^3 + b`. Probeer vooraf te bedenken welk voorschrift bij de hellingsfunctie zou moeten passen. En controleer dan of je gelijk hebt. Het is het leukst om in tweetallen te werken en manier te bedenken om de afgeleide te vinden zonder met differentiequotiënten te werken.

Uitleg

Bij een functie van de vorm `f(x) = x^2` kun je een afgeleide (functie) `f'(x)` opstellen door het differentiequotiënt op het interval `[x,x + h]` te bewerken en dan `h` naar 0 te laten naderen:

`(Delta y)/(Delta x) = ((x + h)^2 - x^2)/h = (2xh + h^2)/h = 2x + h`

Conclusie: de afgeleide van `f(x) = x^2` is `f'(x) = 2x` voor elke waarde van `c`.

Op dezelfde manier kun je aantonen dat de afgeleide van `f(x) = x^3` is `f'(x) = 3x^2` voor elke waarde van `c`.

En zelfs kun je aantonen dat de afgeleide van `f(x) = cx^n` is `f'(x) = ncx^(n-1)` voor elke waarde van `c`.

Dit laatste resultaat is gemakkelijk te onthouden. Voor het bepalen van de afgeleide van dit type functies (machtsfuncties met gehele positieve exponent) hoef je daarom niet langer met differentiequotiënten te worstelen. Je gebruikt het resultaat hierboven: de afgeleide wordt vermenigvuldigd met de exponent van de machtsfunctie en krijgt een nieuwe exponent die precies 1 kleiner is dan die van de machtsfunctie zelf.

De afgeleide van `f(x) = 3x^7` is volgens die methode `f'(x) = 3 * 7x^(7-1) = 21x^6`.
Dat gaat een stuk makkelijker dan met een differentiequotiënt, niet waar?

Je noemt het gebruik maken van dergelijke regels wel differentiëren en de regels zelf heten differentieerregels. Er zijn er nog veel meer.

Neem bijvoorbeeld de constante functie `f(x) = c`.
Je kunt eenvoudig laten zien met behulp van een differentiequotiënt dat daarvan de afgeleide `f'(x) = 0` is.
Dat kun je een tweede differentieerregel noemen.
Hij is ook logisch als je naar de grafiek van deze constante functie kijkt:
van een lijn evenwijdig aan de x-as is de helling overal 0.

Voorlopig is er nog één differentieerregel van belang: de zogenaamde somregel. Die regel luidt:

De afgeleide van de som (of het verschil) van twee functies is de som (het verschil) van de afgeleiden van die functies.

Je gebruikt deze differentieerregels bij het vinden van de afgeleide van een functie zoals
`f(x) = 0,1x^3 - 3x^2 + 25x + 10`.
De afgeleide is: `f'(x) = 0,1 * 3x^(3-1) - 3 * 2x^(2-1) + 25 * 1x^(1-1) + 0 = 0,3x^2 - 6x + 25`.

‡

Opgaven

1. Bij een functie van de vorm `f(x) = cx^2` kun je een afgeleide (functie) `f'(x)` opstellen door het differentiequotiënt op het interval `[x,x + h]` te bewerken.
   1. Doe dat zelf.
   2. Laat je nu `h` naar 0 naderen, dan vind je de afgeleide van `f`. Bepaal de deze afgeleide.
   3. Op deze wijze kun je van alle functies van de vorm `f(x)=cx^n` de afgeleide bepalen (`n` is een willekeurig positief geheel getal): `f'(x)=cnx^(n-1)`. Deze differentieerregel vind je ook in de theorie. Bepaal met behulp van deze algemene regel de afgeleide van `f(x)=3x^5`.


2. Voor het bepalen van de afgeleide (de hellingsfunctie) van een gegeven functie `f` bestaan handige regels die differentieerregels worden genoemd. Bij de Uitleg kun je er een aantal van vinden. Het gebruiken van die regels noem je differentiëren.
   1. De machtsregel helpt bij het differentiëren van machtsfuncties. Bepaal de afgeleide van `f(x) = 12x^5`.
   De andere differentieerregels helpen bij het bepalen van de afgeleide van de som van meerdere functies en bij constanten die je bij een functie optelt. Bekijk Voorbeeld 1.
   2. Bepaal de afgeleide van `g(x) = 12x^5 + 20`.
   3. Bepaal de afgeleide van `h(x) = 12x^5 + 20x^3`.

Theorie

De afgeleide van een functie `y = f(x)` is te bepalen door `h` naar `0` te laten naderen in het differentiequotiënt:

`(Delta y)/(Delta x) = (f(x + h) - f(x))/h`

Voor veel soorten functies zijn hieruit algemene regels af te leiden waarmee je de afgeleide op een eenvoudiger manier kunt vinden. Dergelijke regels heten differentieerregels en het toepassen ervan noem je differentiëren.

Differentieerregel 1 (machtsregel):
De afgeleide van `f(x) = cx^n` is `f'(x) = ncx^(n-1)` voor elke waarde van `c` en voor gehele positieve waarden van `n`.

Differentieerregel 2 (constante-regel):
De afgeleide van een constante (functie) is 0: als `f(x) = c` dan is `f'(x) = 0`.

Differentieerregel 3 (somregel):
De afgeleide van de som (of het verschil) van twee functies is de som (het verschil) van de afgeleiden van die functies: als `f(x) = u(x) +- v(x)` dan is `f'(x) = u'(x) +- v'(x)`.

‡

Voorbeeld 1

Bepaal de afgeleide van de functie `f(x) = x^3 + 4x^2 - 12x - 100`.

Antwoord

Schrijf eerst de functie als een som (verschil) van machtsfuncties en constante functies:

`f(x) = x^3 + 4x^2 - 12x^1 - 100`

De afgeleide is dan:

`f'(x) = 3x^(3-1) + 4 * 2x^(2-1) - 12 * 1x^(1-1) - 0 = 3x^2 + 8x - 12`.

‡

Voorbeeld 2

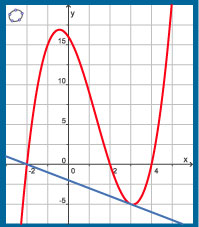
Stel een vergelijking op van de raaklijn aan de grafiek van de functie `g(x) = (x^2 - 4)(x - 4)` voor `x = 3`.

Antwoord

Voor de vergelijking van de raaklijn heb je het hellingsgetal `g'(3)` nodig. Dat kun je met behulp van je grafische rekenmachine vinden. Maar het kan ook met behulp van differentiëren.

Eerst schrijf je het functievoorschrift als een som (verschil) van machtsfuncties en constante functies. Haakjes uitwerken geeft:

`g(x) = x^3 - 4x^2 - 4x^1 + 16`.

De afgeleide is daarom:

`g'(x) = 3x^2 - 4 * 2x^1 - 4 * 1x^0 + 0 = 3x^2 - 8x - 4`.

Je vindt daarmee: `g'(3) = -1`.
En de raaklijn krijgt een vergelijking van de vorm: `y = -1x + b`.
Omdat `g(3) = -5` gaat de raaklijn door `(3,-5)`.
Invullen in de vergelijking van de raaklijn geeft: `-5 = -3 + b` en dus `b = -2`.
De vergelijking van de raaklijn wordt: `y = -x - 2`.

‡

Voorbeeld

De kosten `K` (in euro) bij de productie van `q` eenheden van een bepaald product bedragen:
`K(q) = 0,5q^3 - 4,5q^2 + 40q + 80`.
Er zijn twee waarden van `q` waarin de kosten stijgen met een snelheid van 40 euro per eenheid. Welke twee waarden van `q` zijn dat?

Antwoord

De snelheid waarmee de functiewaarden stijgen afhankelijk van `q` is `K'(q)`.
Nu is: `K'(q) = 1,5q^2 - 9q + 40`.
En dus geldt `K'(q) = 40` als:

`1,5q^2 - 9q + 40 = 40`.

De oplossingen van deze vergelijking zijn `q=0` en `q=6`.

‡

Opgaven

3. Bepaal de afgeleide van de volgende functies door te differentiëren met behulp van de differentieerregels, zie ook Voorbeeld 1. Bepaal telkens de richtingscoëfficiënt van de raaklijn voor `x=1` .
   1. `f(x) = 10x^3 - 60x + 100`
   2. `f(x) = 15 + 2x - 5x^2 - 10x^4`
   3. `f(x) = 1/2x^4 - 4x^2`


4. Gegeven is de functie `y = (x^2 - 4)(x - 6)`.
   1. Een functievoorschrift in deze vorm is handig als je de nulpunten van de functie wilt bepalen. Bereken die nulpunten.
   2. Als je met hellingsgetallen van deze functie wilt werken moet je eerst de haakjes uitwerken. Bepaal de afgeleide `(text(d) y)/(text(d) x)` van deze functie.
   3. Met behulp van deze afgeleide kun je de vergelijking van een raaklijn aan de grafiek opstellen. In Voorbeeld 2 kun je nog eens zien hoe dat gaat. Stel een vergelijking op van de raaklijn aan de grafiek van deze functie voor `x=2`.


5. Gegeven de functie `f(x) = 0,5x^3 - 4,5x^2 + 10x - 35`.
   1. Bepaal de afgeleide van deze functie.
   2. Bereken het hellingsgetal van de raaklijn aan de grafiek van `f` voor `x=0`.
   3. Er zijn punten op de grafiek van `f` waarin de helling de waarde 10 heeft. Bereken de coördinaten van die punten. Bekijk eventueel Voorbeeld 3.

Verwerken

6. Bepaal telkens de afgeleide van de gegeven functie. Bepaal ook het hellingsgetal van de grafiek in `(1,y)`.
   1. `f(x) = x^3 - 4x`
   2. `g(x) = x^4 + 2x^3 - 5x^2 + 12x - 35`
   3. `s(t) = 60t - 4,9t^2`
   4. `H(t) = 2(t^2-4)`
   5. `y = 5 - (x-3)^2`
   6. `P(x) = ax^3 + bx^2 + cx + d`
   7. `TW(q) = 0,5q^3 - 6q^2 - 25q + 112`
   8. `K(x) = (3x^2 - 2a)(ax - 1)`


7. Bepaal van elk van de volgende functies de afgeleide. Bereken vervolgens de punten van de grafiek waar de richtingscoëfficiënt van de raaklijn de waarde 0 heeft. (Eventuele benaderingen in één decimaal nauwkeurig.)
   1. `f(x) = 0,5x^4 - 4x^2`
   2. `TW(q) = -q^3 + 3q^2 + 3q + 6`
   3. `v(t) = t(t - 1)^2`
   4. `TW = 40p - 0,02p^2`


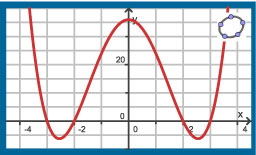8. Je ziet hier de grafiek van de functie `f(x) = (x^2 - 4)(x^2 - 9)`.
   1. Laat zien hoe je uit het functievoorschrift de nulpunten van de grafiek van `f` kunt afleiden.
   2. Bepaal de afgeleide van `f`.
   3. Bereken het snijpunt van de raaklijnen aan de grafiek van `f` voor `x=-2` en voor `x=2`.
   4. Los op: `f'(x)=0`.
   5. Wat betekent het antwoord van d voor de grafiek van `f`?


9. Als een voorwerp wordt afgeschoten met een bepaalde beginsnelheid en onder een bepaalde hoek, dan is zijn baan parabolisch als je geen rekening hoeft te houden met de luchtweerstand. Een voorbeeld van zo’n kogelbaan is de grafiek van de functie `h(x) = 1,5 - 0,01(x - 10)^2`. Hierin is `h` de hoogte van het afgeschoten voorwerp boven de grond (in m) en `x` de afstand over de grond tot recht onder het afgeschoten voorwerp (in m).
   1. Op welke hoogte werd het voorwerp afgeschoten?
   2. Bereken `h'(0)`.
   3. Wat betekent dit getal voor de kogelbaan?
   4. Bereken het punt van de kogelbaan waarin `h(x)=0`.
   5. In het hoogste punt van de kogelbaan is de afgeleide nul. Toch beweegt de kogel daar met een zekere snelheid. Kun je dit verklaren?


10. Voor de productiekosten van een bepaald artikel geldt: `TK = 1200 + 0,2q^2`. Hierin is `q` het aantal geproduceerde eenheden van dat artikel en stelt `TK` de totale kosten in euro voor. De productiekosten per eenheid worden gegeven door `GTK=(TK)/q`. Je noemt dit wel de gemiddelde totale kosten.
    1. Druk de gemiddelde totale kosten uit in `q`.
    2. Met de grafische rekenmachine kun je de grafiek van `GTK` bekijken. Welke verticale asymptoot heeft de grafiek van `GTK`? Welke economische betekenis heeft deze asymptoot?
    3. Je kunt bij deze functie (nog) geen afgeleide bepalen. Maar je kunt er wel een (benadering van de) hellingsgrafiek bij tekenen met je grafische rekenmachine. Teken die hellingsgrafiek en bepaal met behulp daarvan bij welke productie de gemiddelde totale kosten zo laag mogelijk zijn.
    4. Welke waarde benadert de helling van de grafiek van `GTK` als de productie heel erg groot is? En welke betekenis heeft dat voor de productiekosten per eenheid?

Testen

11. Bepaal bij elk van deze functies de afgeleide. Soms moet je eerst het functievoorschrift nog bewerken.
    1. `f(x) = x^6 + 8x - 12`
    2. `f(x) = 3x^4 - 1/2x^2`
    3. `f(x) = -1,5x^3 + 4x`
    4. `f(x) = x(x^2 - 2x)`
    5. `f(x) = -x^5 + 4x^4 + 2x^3 - 1,5x^2 + 8x - 15`
    6. `f(x) = (2x + 1)^2`
    7. `f(x) = 12 - x^2(x - 6)`
    8. `f(x) = (1 - x)^3`


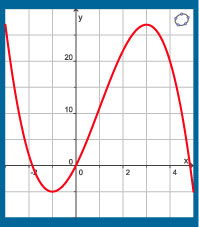12. Dit is (een deel van) de grafiek van de functie `f(x) = 9x + 3x^2 - x^3`.
    1. Bereken het hellingsgetal van deze functie in het punt `(0,0)` met behulp van de afgeleide.
    2. Stel een vergelijking op van de raaklijn aan de grafiek van `f` in het punt `(0,0)`.
    3. Er zijn twee punten op de grafiek van `f` waarin de richtingscoëfficiënt van de raaklijn gelijk is aan 0. Welke twee punten zijn dat?
    4. De grafiek van `f` heeft in een bepaald punt een grootste hellingsgetal. In welk punt is dat?


13. `y` is een functie van `x` waarvoor geldt: `y = x^3 - 25,5x^2 + 180x + 120`.
    1. Bepaal de afgeleide van deze functie.
    2. Deze afgeleide heeft twee nulwaarden. Welke betekenis hebben die nulwaarden voor de functie?
    3. Bereken de nulwaarden van de afgeleide `y'`.
    4. Voor welke waarden van `x` is de functie dalend?