Het begrip afgeleide

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Afgeleide functies > Het begrip afgeleide > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Afgeleide functies > Het begrip afgeleide > Uitleg

Lees eerst de Uitleg goed door.

Opgaven

Voor de afgelegde afstand `a` van een versnellende zeilwagen in meter geldt: `a=1,2t^2` waarin de tijd in seconden is. In de Uitleg zie je een deel van de grafiek bij deze formule. De gemiddelde snelheid in m/s gerekend over de eerste 4 seconden wordt berekend met behulp van een differentiequotiënt.
1. Bereken de gemiddelde snelheid over de eerste 5 seconden.
2. Je gaat nu de snelheid op `t=5` berekenen. Bereken eerst het differentiequotiënt op het interval `[5,5 + h]` en vereenvoudig de gevonden uitdrukking voor `h != 0`.
3. Hoe groot is het differentiaalquotiënt en dus de snelheid op `t=5`?

Voor de afgelegde afstand `a` van een versnellende zeilwagen in meter geldt: `a=1,2t^2` waarin `t` de tijd in seconden is.
1. Je kunt zelf een formule afleiden voor de snelheid als functie van `t`. Stel eerst het differentiequotiënt op het interval `[t,t + h]` op.
2. Als `h` de waarde 0 nadert, krijg je de snelheid voor een willekeurige waarde van `t`. Geef een formule voor de snelheid als functie van `t`.
3. De functie die je hebt gevonden heet de afgeleide van `a(t)`. Welke betekenis heeft `a'(5)` in dit verband?
  1. `a'(5)` is de gemiddelde snelheid in de eerste 5 seconden;
  2. `a'(5)` is de afgelegde weg in de eerste 5 seconden;
  3. `a'(5)` is de snelheid op tijdstip `t=5`
4. Hoe groot is `a'(5)`?
5. Met behulp van de afgeleide kun je vragen beantwoorden als: Op welk tijdstip rijdt de zeilwagen 50 km/h?
  Bereken het antwoord op die vraag in stappen:
  - Bereken hoeveel meter per seconde de snelheid bedraagt.
  - Stel de vergelijking op die je nu moet oplossen.
  - Bereken de oplossing.

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Afgeleide functies > Het begrip afgeleide > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

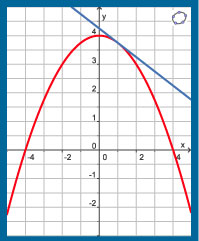Hier zie je de grafiek van de functie `f(x) = 4 - 0,25x^2` met domein `[-5,5]`.
1. De hellingwaarde van de grafiek voor `x=1` kun je bepalen met behulp van je grafische rekenmachine en met behulp van het differentiequotiënt op `[1,1 + h]`. In Voorbeeld 1 kun je nalezen hoe dat in zijn werk gaat.
  Bereken het differentiequotiënt op `[1,1 + h]`.
2. Welke hellingwaarde heeft de grafiek nu voor `x=1`?
3. Deze hellingwaarde is tevens de richtingscoëfficiënt van de raaklijn aan de grafiek voor `x=1`. Stel een vergelijking van die raaklijn op.

Gegeven is de functie `f(x) = 4 - 0,25x^2` met domein `[-5,5]`.
1. Met behulp van het differentiequotiënt op `[x,x + h]` kun je de afgeleide van de functie `f(x)` bepalen. Laat zien hoe dat gaat. Bekijk eventueel Voorbeeld 2.
2. De lijn met vergelijking `y = -2x + 8` lijkt de grafiek te raken. Laat met een berekening zien dat dit inderdaad het geval is.

Bij functies met hogere machten is het berekenen van de afgeleide uit het differentiequotiënt `(f(x+h)-f(x))/h` vaak nogal bewerkelijk. In Voorbeeld 3 kun je nalezen hoe dat in zijn werk gaat bij `f(x)=x^3`.
1. Probeer eerst zelf om de afgeleide van deze functie te bepalen. Controleer dan je antwoord door naar het voorbeeld te kijken.
2. De hellingwaarde voor `x=2` is:
  1. `f(2)=8`
  2. `f'(2)=36`
  3. `f'(2)=12`
3. Er zijn twee punten op de grafiek van `f` waarin de helling de waarde 6,75 heeft. Bereken de coördinaten van deze beide punten.
4. Met de grafische rekenmachine kun je een benadering van de hellingsgrafiek tekenen door in het differentiequotiënt een heel klein getal voor `h` te nemen. Nu je een voorschrift voor de afgeleide hebt, kun je die echter ook rechtstreeks in beeld brengen. Controleer met behulp van je grafische rekenmachine dat beide manieren dezelfde grafiek opleveren.
5. Welke van de volgende uitspraken zijn juist?
  1. Als voor een bepaalde functie `g` geldt dat `g'(0)=0` dan heeft deze functie een uiterste waarde voor `x=0`
  2. Als voor een bepaalde functie `g` geldt dat `g'(0)=0` dan heeft deze functie een horizontale raaklijn voor `x=0`.
  3. Als voor een bepaalde functie `g` geldt dat er een uiterstewaarde is voor `x=0` dan is `g'(0)=0`.
  4. Als voor een bepaalde functie `g` geldt dat de grafiek een horizontale raaklijn heeft voor `x=0` dan is `g'(0)=0`.

Verwerken

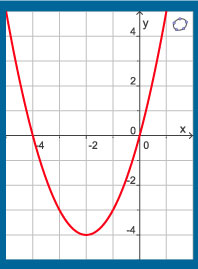Gegeven is de functie `f(x) = x^2 + 4x`.
1. Bereken het hellingsgetal van de grafiek van `f` voor `x=1` met behulp van het differentiequotiënt op het interval `[1,1 + h]`. Controleer je antwoord met de grafische rekenmachine.
2. Stel een functievoorschrift op voor de afgeleide van `f`.
3. Met behulp van `f'(x)` kun je nogmaals de hellingwaarde voor `x=1` berekenen. Doe dat en ga na dat je dezelfde uitkomst krijgt dan bij a.
4. De grafiek van `f'` heeft een nulpunt. Welke betekenis heeft dit punt voor de grafiek van `f`?
5. Bereken de hellingwaarde van de grafiek van `f` in zijn nulpunten.
6. De grafiek van `f` heeft precies één punt waarop de helling 2 is. Bereken de coördinaten van dit punt.

Voor een lichaam in vrije val (bijvoorbeeld een parachutespringer voordat hij zijn valscherm opent) geldt bij benadering `s(t) = 0,5gt^2` waarin `s` de afgelegde afstand in m na `t` seconden is. `g` is een constante, de gravitatieconstante van ongeveer `9,8` m/s².
1. Hoeveel bedraagt de gemiddelde snelheid gedurende de eerste 10 seconden vrije val?
2. De snelheid na 10 seconden vrije val is groter dan de gemiddelde snelheid over de eerste 10 seconden. Laat dit door middel van een berekening zien.
3. Stel een formule op voor de snelheid als functie van `t`.
4. Na hoeveel seconden vrije val beweegt het lichaam met een snelheid van `120` km/h?

Een constante functie heeft als voorschrift `f(x)=c`.
Toon aan dat de afgeleide van een constante functie altijd de waarde 0 heeft.

Een bepaalde autofabrikant maakt als enige een kleine stadsauto. Voor de totale opbrengst van de verkoop van die auto’s geldt: `TO = 900q - 60q^2` waarin `TO` wordt uitgedrukt in duizendtallen en `q` de geplande productieomvang in honderdtallen per jaar voorstelt. Er wordt van uit gegaan dat alle geproduceerde auto’s ook worden verkocht.
1. Stel een functievoorschrift op voor de afgeleide van deze opbrengstfunctie.
2. Welke betekenis heeft `TO'(5)` voor de opbrengstfunctie?
3. De autofabrikant wil onderzoeken hoe groot zijn productieomvang moet zijn om een maximale opbrengst te krijgen. Bereken deze productieomvang met behulp van de afgeleide. Controleer je antwoord met de grafische rekenmachine.

De hoeveelheid van een bepaalde giftige stof in het water van een meertje wordt op minder: de stof breekt op natuurlijke wijze af. Voor die hoeveelheid geldt `H(t) = 20 * 0,8^t` waarin `H` de hoeveelheid in milligram per liter is en `t` de tijd (in dagen) is, die is verstreken sinds de stof in het water terecht kwam.
1. Hoeveel gram per liter is er gemiddeld in de eerste vier dagen verdwenen?
2. De afbreeksnelheid van deze giftige stof is op `t=0` hoger dan op `t=4`. Bepaal beide afbreeksnelheden met je grafische rekenmachine en leg uit waarom ze verschillen.
3. Je zou de afbreeksnelheid ook moeten kunnen berekenen met behulp van een differentiequotiënt. Daarbij doet zich echter een probleem voor. Welk?

Testen

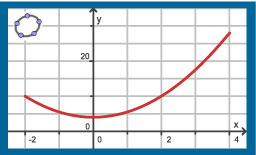Hier zie je grafiek van de functie `f(x) = 1,5x^2 + 4` op het interval `[-2,4]`.
1. Bereken de gemiddelde verandering van `f(x)` op dit interval.
2. Stel een functievoorschrift op voor de afgeleide `f'(x)`.
3. Bereken de veranderingssnelheid van `f(x)` voor `x=2`.
4. Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x=2`.

De kosten `K` (in euro) voor de productie van `q` liter van een bepaalde chemische stof bedragen `K(q) = 0,1q^2 + 0,7q + 12`.
1. Met behulp van het differentiequotiënt over het interval `[q,q+h]` kun je een formule opstellen voor `K'(q)`. Stel die formule op, laat duidelijk zien hoe je te werk gaat.
2. Hoe kun je aan de gevonden afgeleide zien, dat de kosten blijven stijgen bij toenemende `q`?