Totaalbeeld

Samenvatten

Je hebt nu het onderwerp "Kansmodellen" doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

Begrippenlijst:

51: "ja/nee" kans, binomiale kans
52: binomiale kansverdeling — verwachtingswaarde van een binomiale kansverdeling
53: niet binomiale kansmodellen

Activiteitenlijst:

51: "ja/nee"-kansen, binomiale kansen berekenen
52: een binomiale kansverdeling opstellen met de GR — verwachtingswaarde berekenen
53: herkennen wanneer wel en wanneer geen sprake is van een binomiale verdeling — benadering met een binomiaal kansmodel
54: het juiste kansmodel leren kiezen

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Kansmodellen > Totaalbeeld > Achtergronden

Testen

  1. In de nazomer zijn de druiven zover gerijpt dat ze geoogst kunnen worden. De smaak van de druiven wordt aanzienlijk verbeterd als ze nog wat langer kunnen profiteren van de zonnewarmte. Daar staat tegenover dat, als de druiven langer blijven hangen, rekening gehouden moet worden met schade ten gevolge van regenval. Een druiventeler heeft de keus uit twee manieren van oogsten: De druiventeler kan rekenen op een oogst van 12000 kilo. Weerkundigen hebben voorspeld dat voor elke dag van de periode van veertien dagen de kans op een regendag 15% is.
    1. Bereken de opbrengst bij de eerste manier van oogsten.
    2. Bereken de mogelijke opbrengsten en hun kansen bij de tweede manier van oogsten.
    3. Bij welke manier van oogsten heeft de opbrengst de hoogste verwachting?
    4. Bedenk een situatie waarin het toch verstandiger is om voor de andere manier van oogsten te kiezen.

  2. Uit een statistisch onderzoek blijkt dat 40% van de vrouwen van 18 jaar of ouder rookt. Je ontmoet een willekeurige groep van 25 vrouwen die 18 jaar of ouder zijn.
    Bereken met behulp van de statistische gegevens de kans dat er in deze groep 12 of minder vrouwen roken.

  3. Ieder jaar zijn de Nederlandse bungalowparken in het pinksterweekend volgeboekt. Huurders van bungalows dienen dus tijdig te reserveren De eigenaar van een bungalowpark met 16 bungalows weet uit ervaring dat gemiddeld 1 op elke 5 huurders niet komt opdagen. Daarom besluit hij meer huurders in te schrijven dan er bungalows zijn. Hij loopt dan wel het risico op overbezetting, namelijk als er meer huurders komen opdagen dan er bungalows beschikbaar zijn.
    1. Stel dat hij 19 huurders inschrijft. Bereken voor dit geval de kans op overbezetting.
    Natuurlijk is het vervelend om in geval van overbezetting huurders te moeten teleurstellen. De eigenaar wil daarom dat de kans op overbezetting niet groter is dan 10%.
    1. Hoeveel huurders mag hij maximaal inschrijven voor de 16 bungalows?

  4. Pachisi is één van de oudste bordspelen ter wereld en is afkomstig uit India. Het spel lijkt erg veel op "Mens erger je niet". Elke speler heeft vier fiches die hij vanuit het midden van het bord (de char-koni) over de char (de middelste baan van de arm van het Pachisibord die de betreffende speler toebehoort) en dan tegen de wijzers van de klok in langs de zijkanten van alle armen. Tenslotte gaat elke fiche weer via de char terug naar het midden van het bord.
    Bij Pachisi worden zes kaurischelpen gebruikt om mee te gooien en het gaat om het aantal kauri's dat met de opening naar boven ligt. `X` is het aantal kaurischelpen dat boven komt te liggen.
    1. Maak een kansverdeling voor `X`.
    2. Welk aantal kauri's verwacht je bij elke keer gooien met de opening naar boven?
    Bij Pachisi mag je als je 2, 3, 4, 5 of 6 kauri's met de opening naar boven gooit een fiche even zoveel plaatsen verschuiven. Gooi je echter één kauri met de opening naar boven mag je het fiche 10 plaatsen verschuiven en gooi je nul kauri's met de opening naar boven dan mag je het fiche 25 plaatsen verschuiven. `Y` is het aantal plaatsen dat je een fiche per beurt (één worpen met de zes kauri's) mag verplaatsen.
    1. Hoeveel plaatsen verwacht je bij elke keer gooien een fiche te mogen verschuiven?

  5. In de kantine van een bedrijf staat een kofiezetter die geacht wordt in een koffiebekertje 0,15 liter koffie te doen. De hoeveelheid koffie die het apparaat telkens in het kopje giet is normaal verdeeld met een gemiddelde van 0,17 liter en een standaarddeviatie van 0,015 liter.
    1. Hoe groot is de kans dat een koffiebekertje minder dan 0,15 liter koffie bevat?
    2. Tijdens een pauze worden er 40 koppen koffie uit dit apparaat getapt. Hoe groot is de kans dat daarvan hoogstens 4 minder dan 0,15 liter koffie bevatten?

Toepassen

  1. Codes

    Veel informatie wordt tegenwoordig in digitale vorm verzonden. Dat betekent dat informatie met behulp van een reeks énen en nullen wordt doorgegeven. Bij verzending en ontvangst kan er iets misgaan: een verzonden 0 kan opgevangen worden als een 1 of omgekeerd. De coderingstheorie houdt zich bezig met deze problematiek. Lees hierover in

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Kansmodellen > Totaalbeeld > Toepassingen

    Gebruik de gegevens die daarin worden vermeld. Er wordt een een woord van 12 symbolen, dus een reeks van 96 énen en nullen verzonden.
    1. Hoe groot is de kans dat alle symbolen goed worden ontvangen?
    2. Hoe groot is de kans dat er meer dan 94 tekens goed worden ontvangen?
    Het aantal fouten kan verminderd worden door de tekens te herhalen. In plaats van de reeks 1010 verzend je dan bijvoorbeeld 111000111000. Elke 0 en elke 1 wordt drie keer verzonden. Ook nu kan er natuurlijk weer iets misgaan.
    Wanneer de ontvanger 101000111011 ontvangt dan weet hij zeker dat er bij minstens twee tekens iets fout is gegaan; namelijk in het eerste en in het vierde drietal. De kans op twee fouten binnen een groep van drie tekens is veel kleiner dan de kans op één fout. Daarom neem je aan dat 101 verzonden is als 111, en 011 als 111, en 001 als 000, enzovoorts.
    1. Hoe groot is nu de kans nog dat een teken verkeerd wordt ontvangen?
    2. Hoe groot is nu de kans dat alle 96 tekens goed worden ontvangen?

  2. Mantoux-reactie

    Bestudeer de informatie over de Mantoux-reactie op

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Kansmodellen > Totaalbeeld > Toepassingen

    Hoe groot is de kans dat iemand die geen Mantoux-reactie vertoont toch aan TBC lijdt?

Examenopgaven

  1. Enquête

    Opiniepeilingen worden vaak telefonisch gedaan, maar voor bepaalde soorten enquêtes stuurt een onderzoeksbureau enquêteurs met een vragenlijst op pad. Aselect wordt een aantal adressen getrokken. Het onderzoeksbureau laat enquêteurs die adressen bezoeken om de bewoners van die adressen vragen te stellen.
    Voor een onderzoek moeten 1400 adressen worden bezocht. Er zijn hiervoor 4 vaste medewerkers beschikbaar en 16 studenten die dit als bijbaantje hebben. Een vaste medewerker krijgt een groter aantal adressen dan een student. Iedere vaste medewerker krijgt evenveel adressen. Ieder van de 16 studenten krijgt ook een gelijk aantal adressen, maar dat zijn er 30 minder dan het aantal dat een vaste medewerker krijgt.
    1. De 1400 adressen kunnen "precies" verdeeld worden. Laat dit zien door te berekenen hoeveel adressen een vaste medewerker en hoeveel adressen een student krijgt.
    Als er niet 1400 maar 1405 adressen te verdelen zijn, worden eerst de 1400 adressen "precies" verdeeld. De overblijvende 5 adressen worden dan verloot onder de 20 enquêteurs. Daarbij heeft iedereen dezelfde kans op een extra adres, maar niemand krijgt er meer dan één adres bij.
    1. Bereken de kans dat deze 5 adressen allemaal bij de 16 studenten terecht komen.
    Wanneer de enquêteur op een adres komt waar niemand thuis is, probeert hij het later voor de tweede keer. Als ook bij het tweede bezoek niemand thuis is, doet hij bij dit adres nog een derde poging. Die derde keer is ook de laatste keer, zelfs als er dan weer niemand thuis is. Uit ervaring weet men dat de kans dat iemand thuis is de eerste keer het grootst is. Bij de tweede poging is de kans wat kleiner en bij het derde bezoek zelfs veel kleiner.
    Stel dat bij het eerste bezoek op 90% van de adressen iemand thuis is. Bij de adressen waar men de eerste keer niet thuis was, is 80% bij het tweede bezoek wel thuis. Op de adressen waar een derde poging nodig is, is bij dat derde bezoek 40% thuis.
    1. Bereken de kans dat de enquêteur op een adres pas bij het derde bezoek iemand thuis treft.
    2. Het onderzoek wordt gehouden bij 1400 verschillende adressen. Bereken hoeveel keer in totaal er een adres zal worden bezocht voor dit onderzoek.

    (bron: examen wiskunde A1,2 havo 2000, eerste tijdvak, opgave 2)


  2. Casino

    Holland Casino exploiteert in Nederland een aantal casino’s. Elk jaar brengt zij verslag uit over de resultaten van het afgelopen jaar. Onderstaande figuur is gebaseerd op cijfers uit het jaarverslag over 1995. In deze opgave is de gulden de munteenheid (in 2002 vervangen door de euro, de waarde van de gulden was 0,453780216 euro).



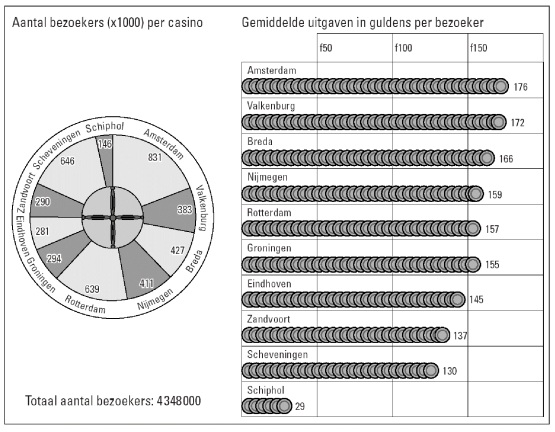
    In deze figuur lezen we onder andere dat Nederlands grootste casino, het casino in Amsterdam, dat jaar 831000 bezoekers trok. Zij gaven daar gemiddeld 176 gulden uit. Dat is vrij veel, want in heel Nederland was het gemiddelde ongeveer 153 gulden.
    1. Toon aan met behulp van de gegevens in de bovenstaande figuur dat het Nederlandse gemiddelde inderdaad ongeveer 153 gulden was.
    In het weekend is het in de casino’s het drukst. Ruim 22% van alle bezoekers komt op zaterdag. We gaan er van uit dat het bezoekersaantal op zaterdag van het Amsterdamse casino normaal verdeeld is met een gemiddelde van 3500 bezoekers en een standaardafwijking van 350 bezoekers.
    1. Als er meer dan 3000 bezoekers zijn, noemt de bedrijfsleiding het "gezellig druk". Bereken hoeveel zaterdagen in een jaar het naar verwachting gezellig druk is in het Amsterdamse casino. Neem aan dat het jaar 52 zaterdagen heeft.
    De volgende figuur komt uit het jaarverslag over 1998 van Holland Casino.



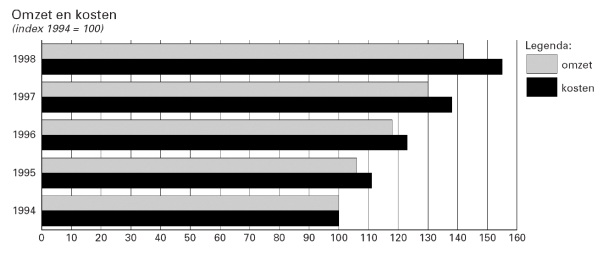
    "Index 1994 = 100" betekent dat alle bedragen vergeleken zijn met de bedragen van 1994.
    Zo heeft de omzet in 1996 het indexcijfer 118. De omzet in 1996 was dus 118% van die in 1994. De omzet steeg tussen 1994 en 1996 dus met 18%. Uit de figuur zou je kunnen concluderen dat de kosten sterker stijgen dan de omzet. Dat zou geen goede ontwikkeling zijn. De winst is immers de omzet min de kosten.
    1. Geef een getallenvoorbeeld waarmee je laat zien dat het met de gegevens uit de figuur toch mogelijk is dat de winst in de periode 1994 – 1998 gestegen is.
    In het casino kun je onder andere spelen aan de roulettetafels. Bij dit spel brengt de bankhouder (de croupier) een ronde schijf aan het draaien waarop 37 genummerde vakjes zitten. De vakjes zijn genummerd van 0 tot en met 36. Dan werpt hij een klein balletje in tegengestelde richting langs de rand van de schijf. Na enige tijd valt het balletje in één van de 37 vakjes. Het nummer van dat vakje is het winnende getal. Voor elk van de 37 vakjes is de kans dat het balletje daarin valt gelijk.
    Hans speelt op een avond de hele tijd alleen op het getal 7, want dat is zijn geluksgetal. Als de 7 niet wint, vindt hij dat niet zo erg. Maar als het balletje wel een keer in het vakje met nummer 7 valt, is zijn hele avond goed. Die avond draait de roulette 250 keer.
    1. Bereken de kans dat het balletje die avond ten minste één keer in het vakje met nummer 7 valt.

    (bron: examen wiskunde A1,2 havo 2001, eerste tijdvak, opgave 5)


  3. Geld uit de muur

    In Nederland staan ongeveer zevenduizend geldautomaten. Bij deze automaten kun je contant geld opnemen van je betaalrekening. De geldautomaten verstrekken uitsluitend biljetten van 10, 20 en 50 euro. De automaat laat je kiezen uit een aantal vaste bedragen of voor de optie "ander bedrag", waarbij je inderdaad een ander bedrag kunt kiezen.
    Wanneer je 60 euro wilt opnemen, kan de geldautomaat dat op verschillende manieren uitkeren. Zo kun je bijvoorbeeld 1 biljet van 50 euro en 1 van 10 euro krijgen. Dat is één manier. Maar ook is mogelijk: 3 biljetten van 20 euro of 6 biljetten van 10 euro.
    1. Op hoeveel verschillende manieren kan de geldautomaat een bedrag van 70 euro uitkeren? Licht je antwoord toe.
    bedrag
    in euro    		aantal
    keer
     1013
     2047
     30 2
     5089
     60 1
     7048
    10014
    120 1
    15012
    200 2
    250 5
    450 1
    750 1
    In een bepaalde geldautomaat in Gouda zijn van elke soort voldoende biljetten aanwezig. In dat geval geeft de automaat de biljetten volgens de volgende regels: In de tabel staan de bedragen die op zekere dag bij deze geldautomaat in Gouda zijn opgenomen.
    1. Bereken hoeveel biljetten van € 20 de geldautomaat op deze dag heeft uitgekeerd.
    Het aantal biljetten van 10 euro dat per dag uit deze automaat gehaald wordt, is bij benadering normaal verdeeld met een gemiddelde van 326 en een standaardafwijking van 41. De geldautomaat wordt dagelijks (ook op zon- en feestdagen) aangevuld tot 400 biljetten van 10 euro.
    Het kan natuurlijk gebeuren dat alle biljetten van 10 euro op zijn voordat de automaat weer wordt aangevuld.
    1. Bereken op hoeveel dagen van een jaar dat naar verwachting zal gebeuren.
    Ook het aantal biljetten van 50 euro dat per dag uit deze automaat gehaald wordt, is bij benadering normaal verdeeld. Het gemiddelde aantal dagelijks uitgekeerde biljetten is 140 en de automaat wordt dagelijks aangevuld tot 175 biljetten van € 50. Op 1,5% van de dagen is dat niet voldoende.
    1. Bereken de standaardafwijking van het dagelijks aantal uitgekeerde biljetten van 50 euro. Rond af op één decimaal.

    (bron: examen wiskunde A1,2 havo 2005, eerste tijdvak, opgave 2, gedeelte)

  4. Kleurenblinde en glasbak

    Ongeveer een half miljoen Nederlanders is kleurenblind. Een kleurenblinde ziet (bijna) geen verschil tussen (bepaalde) kleuren. Gekleurde flessen zijn groen of bruin. Sommige kleurenblinden zien geen verschil tussen groen en bruin. Zij staan met hun lege flessen voor de glasbak en weten niet of ze een gekleurde fles in het gat voor groen glas of in het gat voor bruin glas moeten gooien.
    Peter is kleurenblind. Hij kan de groene en de bruine flessen niet van elkaar onderscheiden. Als Peter met zijn lege flessen bij de glasbak komt, gooit hij de witte flessen altijd in het juiste gat. Bij een gekleurde fles kiest hij aselect tussen het gat voor groen en het gat voor bruin. De kans dat een groene of bruine fles in het goede gat terechtkomt is dus 0,5.
    Peter brengt 100 lege flessen naar de glasbak. De helft van zijn flessen is van wit glas. Bij de andere helft zijn zowel groene als bruine flessen
    1. Laat zien dat naar verwachting 75 van de 100 flessen in het goede gat terechtkomen.
    Uit a volgt: de kans dat een fles in het goede gat terechtkomt is 75% als Peter de witte flessen altijd goed gooit en bij elke gekleurde fles aselect kiest tussen het gat voor groen en het gat voor bruin. Uit onderzoek is gebleken dat van de flessen in de glasbak 50% wit, 40% groen en 10% bruin is. Neem aan dat dit ook voor de flessen van Peter geldt.
    Peter kan de kans dat hij een fles in het goede gat gooit, hoger krijgen dan 75%. Hij gooit de witte flessen allemaal in het goede gat. Hij concludeert uit het onderzoek dat van de gekleurde flessen 4/5 deel groen en 1/5 deel bruin is. In die verhouding gaat hij de gekleurde flessen in de gaten gooien. Elke gekleurde fles heeft dan kans 4/5 om in het gat voor groen terecht te komen en kans 1/5 om in het gat voor bruin terecht te komen.
    1. Bereken voor deze werkwijze de kans dat een willekeurige fles in het goede gat terechtkomt.
    2. Er bestaan nog betere werkwijzen voor Peter. In zo’n werkwijze is de kans dus nog groter dat een fles in het goede gat terechtkomt. Geef een voorbeeld van zo’n werkwijze en toon aan dat deze beter is.

    (bron: examen wiskunde A1,2 havo 2001, eerste tijdvak, opgave 3)

  5. Vlippo's

    Om de verkoop van zijn knabbelchips te bevorderen is een chipsfabrikant een reclameactie gestart waarbij in elke zak één vlippo wordt gestopt. Dat is een plastic schijfje waar een leuk plaatje op staat. Er worden verschillende vlippo's voor deze actie gebruikt. Sommige mensen proberen al deze vlippo's te verzamelen. De kans dat je een bepaalde vlippo in een zak knabbelchips aantreft, is voor alle verschillende vlippo's even groot.
    We gaan eerst uit van de situatie waarin de fabrikant maar twee verschillende vlippo's gebruikt. Een vlippoverzamelaar heeft vier zakken knabbelchips gekocht.
    1. Bereken de kans dat de vlippo's in deze vier zakken allemaal hetzelfde zijn.
    2. Bereken de kans dat de vlippoverzamelaar pas bij het openen van de derde zak de twee verschillende vlippo’s te pakken heeft.
    We bekijken nu de situatie waarin de chipsfabrikant vijf verschillende vlippo's gebruikt. Een vlippoverzamelaar beweert dat hij dan maar vijf zakken knabbelchips hoeft te kopen om de vijf verschillende vlippo's daarin aan te treffen.
    Zijn vriend is het daar niet mee eens. De eerste zak levert natuurlijk altijd een vlippo op die je nog niet hebt, maar de kans dat er in de tweede zak ook een vlippo zit die je nog niet hebt, is maar 4/5. En daarna wordt de kans steeds kleiner.
    1. Bereken met behulp van bovenstaande redenering de kans dat je in vijf zakken de vijf verschillende vlippo’s aantreft.
    We bekijken nog een voorbeeld.
    Als er in totaal 8 verschillende vlippo's zijn, dan zou het natuurlijk leuk zijn als je die alle 8 hebt na het kopen van precies 8 zakken knabbelchips. De kans dat zoiets gebeurt, is klein.
    Wiskundigen hebben uitgerekend dat de kans daarop is: `(8!)/(8^8) ~~ 0,002`.
    Er is ook een formule voor het algemene geval. Er zijn dan `n` verschillende vlippo's. De kans `P` dat je die alle `n` hebt na het kopen van precies `n` zakken knabbelchips wordt gegeven door de formule:

    `P = (n!)/(n^n)`

    Hoe groter het aantal verschillende vlippo's `n` wordt, hoe kleiner die kans `P`. De chipsfabrikant wil wel zo veel mogelijk verschillende vlippo's, maar hij zorgt er voor dat de kans `P` groter is dan 0,00001.
    1. Hoeveel verschillende vlippo’s kan de chipsfabrikant dan maximaal gebruiken? Licht je antwoord toe.

    (bron: examen wiskunde A1,2 havo 2003, eerste tijdvak, opgave 4)