
Binomiale kansverdeling

Inleiding
Plaatjes zoals dit worden gebruikt om te onderzoeken of iemand kleurenblind is. Kleurenblindheid komt voor bij 8% van de westerse mannen en 0,4% van de westerse vrouwen. Via de website www.kleurenblindheid.nl kun je er meer over te weten komen.
Of iemand kleurenblind is kun je niet aan zijn uiterlijk zien, dus je kunt je bijvoorbeeld afvragen hoe groot de kans is dat er kleurenblinden in jouw klas zitten. En hoeveel je er dan verwacht...
Je leert nu:
- binomiale kansenverdelingen snel opstellen;
- rekenen met binomiale kansen;
- een formule voor de verwachting van een binomiale verdeling.
Je kunt al:
- (binomiale) kansen berekenen;
- verwachting bij een kansverdeling berekenen.
Verkennen
Bekijk de informatie over kleurenblindheid hierboven. Gebruik eventueel meer actuele informatie.
> Hoe groot is de kans dat er in een klas van de 10 jongens er 2 kleurenblind zijn?
> Hoe groot is de kans dat er in een klas van 10 jongens en 15 meisjes 2 leerlingen kleurenblind zijn?
> Hoeveel kleurenblinden verwacht je in zo'n klas?
Uitleg
Kleurenblindheid komt voor bij 8% van de westerse mannen.
Of iemand kleurenblind is kun je niet aan zijn uiterlijk zien, dus iedere westerse man die je tegenkomt (en verder niet kent) heeft voor jou een kans van 0,08 om kleurenblind te zijn. Vraag je een willekeurige westerse man of hij kleurenblind is of niet, dan doe je een kansexperiment met precies twee uitkomsten: "nee" als hij niet kleurenblind is en "ja" als dit wel het geval is.
Vraag je 10 westerse mannen naar kleurenblindheid dan voer je dit experiment 10 keer uit: je herhaalt 10 keer hetzelfde experiment.
Noem je de bijbehorende variabele K, dan is de kans dat er 2 kleurenblinden bij zijn:
P(K = 2 | n = 10 en p = 0,08) = 0,082 · 0,928 · ≈ 0,1478
 |
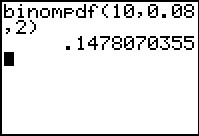 |
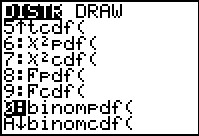
Je grafische rekenmachine heeft voor deze berekening een kansfunctie ingebouwd.
Je rekenmachine noemt dit: "binomial probability distribution function".
Daarbij hoef je alleen het aantal herhalingen (10), de kans op "ja" (0,08) en de gewenste waarde van de stochast (2) in te voeren
om direct de kans P(K = 2 | n = 10 en p = 0,08) te krijgen.
Dat de kans op 2 kleurenblinden in deze steekproef zo klein is komt omdat je verwachtingswaarde bij een binomiaal kansmodel ook gewoon 8% van 10 (de steekproefgrootte) is: 0,08 · 10 = 0,8.
Gemiddeld zijn er in een steekproef van 10 Westerse mannen 0,8 kleurenblinden.
K is de toevalsvariabele die het aantal kleurenblinden in een steekproef van 10 westerse mannen aangeeft.
Vraag je nu naar de kans op hoogstens 2 kleurenblinden in de steekproef dan moet je meerdere kansen optellen:
P(K ≤ 2 | n = 10 en p = 0,08) = P(K = 0) + P(K = 1) + P(K = 2).
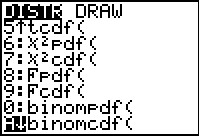
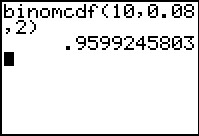
Nu heb je wel gezien dat je rekenmachine deze drie kansen snel kan bepalen, maar er is ook een afzonderlijke functie gemaakt voor "hoogstens"-kansen. Dat noem je een cumulatieve kansverdeling.
Je rekenmachine noemt dit: "binomial cumulative distribution function".
In de GR-plaatjes zie je hoe dit werkt.
‡
Opgaven
-
In de Uitleg wordt besproken hoe je bij het berekenen van binomiale kansen de kansdverdelingen van de grafische rekenmachine kunt inzetten.
- Werk van het practicum "Kansverdelingen met de grafische rekenmachine" het gedeelte over de binomiale verdeling door.
- Reken zelf de kans op 2 kleurenblinden in een groep van 10 westerse mannen op beide manieren uit.
- Bereken de kans op hoogstens 2 kleurenblinden in die groep.
- Hoe groot is de kans op minder dan 2 kleurenblinden in die groep?
-
Voor binomiale kansen op hoogstens een bepaald aantal heeft de rekenmachine een speciale kansfunctie. Voor binomiale kansen op minstens een bepaald aantal is dat niet het geval.
Stel je voor dat je de kans op minstens 2 kleurenblinden in een groep van 10 westerse mannen wilt berekenen.
-
Waarom is deze kans samen met de kansen op 0 of 1 kleurenblinden gelijk aan 1?
-
Bereken de kans op 0 of 1 kleurenblinden in die groep.
-
Bereken nu de kans op minstens 2 kleurenblinden in die groep.
-
Je moet 8 vierkeuzevragen beantwoorden. Dat doe je op de gok, want je weet geen enkel antwoord.
`X` is het aantal vragen dat je goed beantwoordt.
-
Maak op je grafische rekenmachine met behulp van het kansverdelingenmenu een kansverdeling van `X`.
-
Bereken met behulp van die kansverdeling de kans dat je hoogstens 3 vragen goed hebt.
-
Bereken die kans nog eens, maar nu met behulp van de cumulatieve binomiale kansverdeling.
-
Bereken ook op deze beide manieren de kans dat je minstens 3 vragen goed hebt.
Theorie
Als je een "ja/nee"-kansexperiment n keer herhaalt en X stelt het aantal successen (het aantal keren "ja") daarbij voor, dan heeft X een binomiale kansverdeling. Een binomiaal kansexperiment bestaat dus uit n gelijke onafhankelijke experimenten met elk precies twee uitkomsten.
De kans op k successen is P(X = k) = · pk · (1 – p)n – k.
Ook nu is p de kans op "succes" en verder is 0 ≤ k ≤ n.
De variabelen n en p noem je de parameters van de binomiale verdeling.
Voor een binomiaal verdeelde stochast met parameters n en p geldt
- de verwachtingswaarde is: E(X) = n · p
Je grafische rekenmachine heeft een tweetal ingebouwde functies om binomiale kansen snel te berekenen.
Voor kansen van de vorm P(X = k) gebruik je de binomial probability distribution function.
Voor kansen van de vorm P(X ≤ k) gebruik je de binomial cumulative distribution function.
Voor kansen zoals P(X < k), P(X > k) en P(X ≥ k) reken je om naar de voorgaande vorm. Bekijk de voorbeelden!
‡
Voorbeeld 1
Je werpt met 10 dobbelstenen. Hoe groot is de kans dat er 4 zessen boven komen te liggen?
En hoe groot is de kans dat er hoogstens 4 zessen boven komen te liggen?
Antwoord
Het aantal zessen dat boven komt is een binomiale toevalsvariabele X met parameters n = 10 en p = .
De gevraagde kans is: P(X = 4 | n = 10 en p = ).
Je kunt deze kans zelf berekenen:
P(X = 4 | n = 10 en p = ) = ≈ 0,0543.
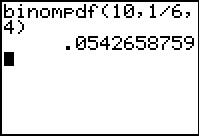
De grafische rekenmachine kan deze kans ook in één keer voor je berekenen.
Dat is zeker handig als je de kans op hoogstens 4 zessen wilt weten. Want in plaats van de kansen voor X = 0, 1, 2, 3 en 4 afzonderlijk te berekenen en dan op te tellen, kan de GR dit in één keer.
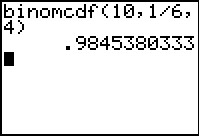
De kans op hoogstens 4 zessen is: P(X ≤ 4 | n = 10 en p = ) ≈ 0,9845.
‡
Voorbeeld 2
Je werpt met 10 dobbelstenen. X geeft het aantal zessen aan dat boven komt te liggen.
Stel een kansverdeling op voor X en bereken de verwachtingswaarde.
Antwoord
X is een binomiale toevalsvariabele met parameters n = 10 en p = .
Je moet nu de kansen bepalen voor X = 0, 1, 2, 3, ..., 10.
Het gaat om kansen van de vorm P(X = x | n = 10 en p = ).
Voer je dit in de grafische rekenmachine in als functie, dan maakt hij de bijbehorende tabel met uitkomsten. De GR maakt dus deze kansverdeling voor je.
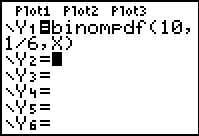
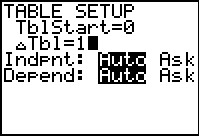
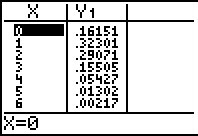
De verwachtingswaarde is E(X) = n · p = 10 · = 1 dobbelstenen.
‡
Voorbeeld 3
Uit onderzoek blijkt dat 8% van de westerse mannen kleurenblind is.
Je vraagt 50 willekeurig gekozen westerse mannen of ze kleurenblind zijn.
Hoeveel kleurenblinde mannen verwacht je in jouw steekproef aan te treffen?
Hoe groot is de kans dat je meer dan vier kleurenblinde mannen in je steekproef aantreft?
Antwoord
Stel K is het aantal kleurenblinde mannen in de steekproef.
K is binomiaal verdeeld met parameters n = 50 en p = 0,08.
De verwachtingswaarde is: E(K) = n · p = 50 · 0,08 = 4 mannen.
De kans op X > 4 kun je zo opschrijven: P(K > 4 | n = 50 en p = 0,08).
Deze kans is gelijk aan: 1 – P(K ≤ 4 | n = 50 en p = 0,08).
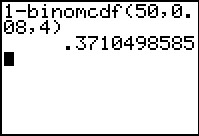 Je grafische rekenmachine kan die kans voor je berekenen:
Je grafische rekenmachine kan die kans voor je berekenen:
P(K > 4 | n = 50 en p = 0,08) =
= 1 – P(K ≤ 4 | n = 50 en p = 0,08) ≈ 0,3710.
‡
Opgaven
-
Bekijk in de Voorbeeld 1 hoe je een binomiale kans noteert en met de grafische rekenmachine kunt vinden.
Neem aan dat `X` het aantal zessen is dat je met 10 dobbelstenen kunt gooien.
-
Wat zijn de parameters van `X`?
-
Hoe groot is de kans op 5 zessen? Noteer die kans op de juiste manier en bepaal hem met de grafische rekenmachine.
-
In Voorbeeld 2 kun je zien hoe je een kansverdeling van `X` kunt maken. Doe dit zelf.
-
Bereken met behulp van deze kansverdeling de kans op hoogstens 3 zessen.
-
Bepaal die kans ook met behulp van de cumulatieve binomiale verdeling.
-
Bepaal op beide manieren de kans op minstens 3 zessen.
-
Neem aan dat `X` een binomiaal verdeelde toevalsvariabele is. Bereken de volgende kansen in vier decimalen nauwkeurig.
- `text(P)(X <= 10 | n = 40 text( en ) p = 0,30)`
- `text(P)(X > 10 | n = 40 text( en ) p = 0,30)`
- `text(P)(X >= 10 | n = 40 text( en ) p = 0,30)`
- `text(P)(X = 10 | n = 40 text( en ) p = 0,30)`
- `text(P)(6 < X < 10 | n = 40 text( en ) p = 0,30)`
-
In Voorbeeld 3 zie je hoe je de verwachting van een binomiale toevalsvariabele berekent.
Bij een toets moet je 50 meerkeuzevragen beantwoorden. Je hebt steeds de keuze
uit vier antwoorden. Slechts één antwoord is goed. Als je 30 of meer vragen goed
hebt beantwoord, krijg je een voldoende.
- Wat is de kans dat je een voldoende haalt als je de antwoorden lukraak invult?
- Hoeveel vragen verwacht je goed te hebben als je de antwoorden lukraak invult?
- Stel dat er 20 makkelijke vragen bij zitten, die je zo weet. De rest vul je lukraak in. Wat is nu je kans op een voldoende?
- Hoeveel vragen zul je in de situatie beschreven in c naar verwachting goed hebben?
-
Neem aan dat 8% van de mannen kleurenblind is.
Je onderzoekt 50 aselect getrokken mannen.
- Hoeveel kleurenblinden verwacht je daarbij?
- Bereken de kans dat er meer dan 5 kleurenblinde mannen bij zijn.
Verwerken
-
Neem aan dat `X` een binomiaal verdeelde toevalsvariabele is. Bereken de volgende kansen in vier decimalen nauwkeurig.
- `text(P)(X <= 6 | n = 20 text( en ) p = 0,35)`
- `text(P)(X < 5 | n = 12 text( en ) p = 0,15)`
- `text(P)(X > 30 | n = 100 text( en ) p = 0,35)`
- `text(P)(X = 3 | n = 10 text( en ) p = 0,25)`
- `text(P)(12 < X <= 16 | n = 17 text( en ) p = 0,85)`
 Bij roulette wordt bij ieder spel een schijf met vakjes, die genummerd zijn van 0
tot en met 36, aan het draaien gebracht. De croupier werpt daarna een balletje
tegen de draairichting van de schijf in. Na enige tijd blijft het balletje in één van
de 37 vakjes liggen. Het nummer van dat vakje is dan het winnende nummer.
Neem aan dat bij elk spel alle nummers gelijke kansen hebben om het winnende
nummer te worden.
Bij roulette wordt bij ieder spel een schijf met vakjes, die genummerd zijn van 0
tot en met 36, aan het draaien gebracht. De croupier werpt daarna een balletje
tegen de draairichting van de schijf in. Na enige tijd blijft het balletje in één van
de 37 vakjes liggen. Het nummer van dat vakje is dan het winnende nummer.
Neem aan dat bij elk spel alle nummers gelijke kansen hebben om het winnende
nummer te worden.
Je speelt een serie van 50 spelen. Bereken (in drie decimalen nauwkeurig) de kans
dat nummer 10 in ten hoogste één van deze 50 spelen het winnende nummer
zal zijn.
-
Bij 25% 28 van de baby’s diemet een bepaalde hartafwijking worden geboren, blijkt
in het eerste levensjaar een complicatie op te treden. In een bepaald jaar worden
15 baby’s met deze hartafwijking geboren.
- Hoe groot is de kans dat er bij hoogstens drie baby’s een complicatie optreedt?
- Hoe groot is de kans dat er bij meer dan tien baby’s een complicatie optreedt?
- Bij hoeveel van deze baby’s zal naar verwachting de complicatie optreden?
-
Gegeven zijn de vazen V1 en V2.
V1 bevat 8 rode en 2 witte knikkers.
V2 bevat 3 rode en 6 witte knikkers.
Je trekt aselect en met terugleggen uit V1 en uit V2 één knikker. Van beide
getrokken knikkers wordt de kleur genoteerd. Deze trekking wordt tien maal
uitgevoerd.
Bereken in drie decimalen nauwkeurig de kans dat bij meer dan vijf van de tien
trekkingen de twee getrokken knikkers van kleur verschillen.
-
In een fabriek worden batterijen gemaakt. Het bedrijf heeft zichzelf als kwaliteitseis
gesteld dat hoogstens 1% van een partij defect mag zijn. Voordat een partij
verkocht wordt, neemt men een steekproef van 100 exemplaren. Als van deze
100 baterijen er meer dan 1 defect is, wordt de partij afgekeurd. Op een zeker
moment wil men een partij van 7000 batterijen verzenden.
-
Hoe groot is de kans dat deze partij wordt afgekeurd als het bedrijf nog juist aan de kwaliteitseis voldoet?
-
In de steekproef van 100 ontdekt men 3 defecte versterkers. De partij wordt afgekeurd. Er is een kleine kans dat dit ten onrechte gebeurt. Bereken die kans.
-
Er wordt `n` maal met een zuivere dobbelsteen geworpen. Het aantal drieën onder
deze worpen wordt geteld.
-
Na hoeveel experimenten verwacht je wel eenmaal een drie te hebben geworpen?
-
Bereken de verwachting van het aantal drieën na 30 worpen.
-
Hoe groot is de kans dat die verwachting bij b ook echt uitkomt?
Testen
-
Als je toegelaten wilt worden tot de pilotenopleiding word je aan een zware
psychologische test onderworpen. De kans dat iemand de eerste keer voor zo’n
test slaagt is 10%. Aan de toets nemen 25 kandidaten deel.
- Bereken de kans dat minstens vijf van deze kandidaten worden toegelaten tot de opleiding.
- Hoeveel kandidaten verwacht je dat er gemiddeld in de eerste ronde worden toegelaten?
-
Neem aan, dat de kans op de geboorte van een meisje gelijk is aan de kans dat er
een jongen wordt geboren. Van een gezin is slechts bekend dat er zeven kinderen
zijn.
Bereken de kans dat er in het gezin hoogstens drie jongens zijn.








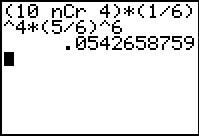




 Bij roulette wordt bij ieder spel een schijf met vakjes, die genummerd zijn van 0
tot en met 36, aan het draaien gebracht. De croupier werpt daarna een balletje
tegen de draairichting van de schijf in. Na enige tijd blijft het balletje in één van
de 37 vakjes liggen. Het nummer van dat vakje is dan het winnende nummer.
Neem aan dat bij elk spel alle nummers gelijke kansen hebben om het winnende
nummer te worden.
Bij roulette wordt bij ieder spel een schijf met vakjes, die genummerd zijn van 0
tot en met 36, aan het draaien gebracht. De croupier werpt daarna een balletje
tegen de draairichting van de schijf in. Na enige tijd blijft het balletje in één van
de 37 vakjes liggen. Het nummer van dat vakje is dan het winnende nummer.
Neem aan dat bij elk spel alle nummers gelijke kansen hebben om het winnende
nummer te worden.