Ja/nee kansen

Inleiding

Bij meerkeuzevragen (multiple choice) is maar één van de (bijvoorbeeld) vijf mogelijke antwoorden goed. Bij elke vraag heb je (als je het antwoord niet weet) een kans van 1/5 dat je het antwoord goed gokt.
De kans op een goed antwoord is dan 1/5, de kans op een fout antwoord 4/5.
Er zijn maar twee mogelijkheden per vraag: "goed" of "fout".
Maar hoe zit het met de kansen als je meerdere van dit soort vragen krijgt (en je weet er niet één)?

Je leert nu:

• ja/nee kansen berekenen;
• werken met combinaties om ja/nee kansen te berekenen.

Je kunt al:

• kansbomen maken om kansproblemen op te lossen;
• combinaties gebruiken bij telproblemen.

Verkennen

Je krijgt 10 van dit soort vragen krijgt (en je weet er niet één).

> Kun je een kansboom maken voor 10 vragen?
> Hoe groot is de kans dat je de eerste 4 van de 10 goed hebt?
> Hoe groot is de kans dat je er precies 4 van de 10 goed hebt?
> Hoe groot is de kans dat je er minstens 4 van de 10 goed hebt?

Uitleg

Bij een bepaalde soort meerkeuzevragen is één van de vijf mogelijke antwoorden goed. Bij elke vraag heb je (als je het antwoord niet weet) een kans van 1/5 dat je het antwoord goed gokt.
De kans op een goed antwoord is dan 1/5, de kans op een fout antwoord 4/5. Er zijn maar twee mogelijkheden per vraag: "goed" of "fout".
Maar hoe zit het met de kansen als je 10 van dit soort vragen krijgt (en je weet er niet één)?

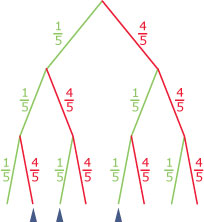Krijg je er bijvoorbeeld 3 dan kun je een kansboom maken zoals deze. Je ziet dat de kans op 2 goed van de drie vragen (bij zuiver gokken) gelijk is aan:
P(X = 2) = $\frac{1}{5}\cdot \frac{1}{5}\cdot \frac{4}{5}$ + $\frac{1}{5}\cdot \frac{4}{5}\cdot \frac{1}{5}$ + $\frac{4}{5}\cdot \frac{1}{5}\cdot \frac{1}{5}$ = $\frac{1}{5}\cdot \frac{1}{5}\cdot \frac{4}{5}$ · 3.
Je ziet dat er drie manieren zijn om twee van de drie vragen goed (G) te hebben en één fout (F), namelijk: GGF, GFG, FGG.

Heb je met tien vragen te maken dan wordt een boomdiagram onoverzichtelijk. Om de kans op 7 vragen goed van de 10 te berekenen moet je dan het aantal mogelijke volgordes met 7 keer een G en 3 keer een F beredeneren.

Om de kans op 7 vragen goed van de 10 te berekenen bedenk je dan eerst dat de kans op één bepaalde volgorde, bijvoorbeeld op GGGGGGGFFF, gelijk is aan ${\left(\frac{1}{5}\right)}^7\cdot {\left(\frac{4}{5}\right)}^3$.

Vervolgens beredeneer je het aantal volgordes met 7 keer een G en 3 keer een F.
Dat doe je met behulp van combinaties: je kiest uit een groep van 10 (7 letters G en 3 letters F) willekeurig 7 letters, waarbij hun onderlinge volgorde niet van belang is.
Dat kun je doen op $\left(\begin{array}{c}10\\ 7\end{array}\right)$ = 120 manieren.

De gevraagde kans wordt: P(X = 7) = $\left(\begin{array}{c}10\\ 7\end{array}\right)$ · ${\left(\frac{1}{5}\right)}^7\cdot {\left(\frac{4}{5}\right)}^3$ ≈ 0,000786.

Een hele kleine kans, maar dat ligt voor de hand...

‡

Opgaven

1. In de Uitleg staat een situatie beschreven waarin 10 vierkeuzevragen op de gok worden ingevuld.
   1. Hoe groot is de kans dat je alle 10 die vierkeuzevragen goed beantwoordt?
   2. Hoe groot is de kans dat je ze alle 10 fout hebt?
   3. Hoe groot is de kans dat je de eerste 7 goed hebt en de rest fout?
   4. Hoe groot is de kans dat je de eerste fout hebt, dan weer 7 goed en vervolgens de rest fout?
   5. Op hoeveel manieren kun je 7 vragen goed en de rest fout hebben? Hoe groot is de kans daarop?


2. Er wordt driemaal met een zuivere dobbelsteen geworpen.
   1. Bereken de kans op drie vijven.
   2. Bereken de kans op geen zessen.
   3. Bereken de kans op tweemaal een drie.


3. In een vaas zitten 5 rode en 10 witte knikkers. Jan haalt na elkaar en met terugleggen aselect 3 knikkers uit de vaas.
   1. Hoe groot is de kans dat daar twee rode knikkers bij zitten?
   Mien haalt tegelijk aselect drie knikkers uit de vaas.
   2. Hoe groot is de kans dat daar twee rode knikkers bij zitten?

Theorie

Bij bepaalde kansproblemen gaat het om situaties waarbij:

• er sprake is van een serie dezelfde deelexperimenten;
• elk deelexperiment precies twee uitkomsten heeft: "ja" of "nee" oftewel "wel" of "niet" een bepaalde eigenschap hebben;
• bij elk deelexperiment steeds de kans op "ja" hetzelfde is en de kans op "nee" hetzelfde is;

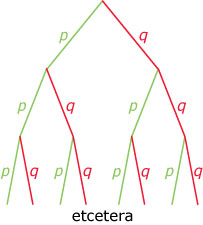
Je spreekt dan van een binomiaal kansprobleem.
In de bijbehorende kansboom zijn dan in elke laag de kansen hetzelfde.

Als bij elk deelexperiment de kans op "ja" p is, dan is de kans op "nee" q = 1 – p.
Herhaal je dit deelexperiment n keer dan is de kans op k keer "ja" gelijk aan:

P(X = k) = $\left(\begin{array}{c}n\\ k\end{array}\right)$ · p^k · q^n – k

Hierin geeft $\left(\begin{array}{c}n\\ k\end{array}\right)$ het aantal mogelijke volgordes aan bij k keer "ja" en n – k keer "nee". Dit is het aantal combinaties van k uit n.

‡

Voorbeeld 1

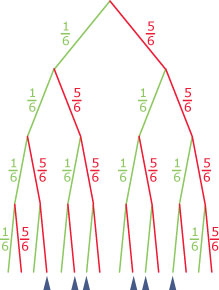
Je werpt met vier dobbelstenen en telt het aantal keren dat er een 6 boven ligt. Hoe groot is de kans op twee zessen?
Waarom is hier sprake van een binomiaal kansprobleem?
Bereken de gevraagde kans.

Antwoord

Omdat de dobbelstenen niet door elkaar beïnvloed worden kun je hier spreken van een herhaling van het werpen met één dobbelsteen. Bij elke dobbelsteen heb je een kans van 1/6 op "zes" en 5/6 op "geen zes", die kans is telkens hetzelfde. Dus is het een binomiaal kansprobleem.

Met een kansboom vind je gemakkelijk de gevraagde kans:

P(X = 2) = ($\frac{1}{6}$)² · ($\frac{5}{6}$)² · 6 = $\frac{25}{216}$

Het aantal mogelijkheden kun je ook berekenen met combinaties: $\left(\begin{array}{c}4\\ 2\end{array}\right)$ = 6.
Dan heb je geen kansboom nodig.

‡

Voorbeeld 2

Je beantwoordt volledig op de gok 20 vierkeuzevragen. Van de vier keuzes per vraag is er telkens maar één goed.
Hoe groot is de kans dat je er 6 goed hebt?

Antwoord

Elke vraag heb je een kans van 0,25 op "goed" en een kans van 1 – 0,25 = 0,75 op "fout". Verder herhaal je dit "spel" 20 keer met steeds dezelfde kansen.
Het is daarom een binomiaal kansprobleem.

De gevraagde kans is: P(X = 6) = 0,25⁶ · 0,75¹⁴ · $\left(\begin{array}{c}20\\ 6\end{array}\right)$ ≈ 0,1686.

‡

Voorbeeld 3

Je beantwoordt volledig op de gok 20 vierkeuzevragen. Van de vier keuzes per vraag is er telkens maar één goed.
Hoe groot is de kans dat je er hoogstens 3 goed hebt?

Antwoord

Net als in Voorbeeld 2 is hier sprake van een binomiaal kansprobleem.
Als X het aantal goede vragen is, dan gaat het nu om de kans: P(X ≤ 3).
Deze kans bereken je zo: P(X ≤ 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3).
Nu is:

• P(X = 0) = 0,75²⁰
• P(X = 1) = 0,25 · 0,75¹⁹ · 20
• P(X = 2) = 0,25² · 0,75¹⁹ · $\left(\begin{array}{c}20\\ 2\end{array}\right)$
• P(X = 3) = 0,25³ · 0,75¹⁷ · $\left(\begin{array}{c}20\\ 3\end{array}\right)$

Dus P(X ≤ 3) ≈ 0,2252.

‡

Opgaven

4. Bekijk in de Theorie wat een binomiaal kansprobleem is. In welke van de volgende gevallen is er van een binomiaal kansprobleem sprake?
   1. Een lijst van 20 vierkeuzevragen wordt puur op de gok ingevuld, maar één antwoord is het juiste. Hoe groot is de kans op 8 vragen goed?
   2. Er wordt 12 keer met een dobbelsteen geworpen. Hoe groot is de kans dat er 5 keer een 6 wordt gegooid.
   3. Uit een vaas met 5 rode en 10 witte knikkers wordt aselect zonder terugleggen 4 knikkers getrokken. Hoe groot is de kans op 3 witte?
   4. Uit een vaas met 5 rode en 10 witte knikkers wordt aselect met terugleggen 4 knikkers getrokken. Hoe groot is de kans op 3 witte?
   5. Je schiet 30 maal met een pijltje op een dartboard. Je hebt telkens 20% kans om de roos te raken. Hoe groot is de kans dat je dit vier keer doet?
   6. In de voetbaltoto moet je per wedstrijd kiezen uit "winst (voor de thuisploeg)", "verlies", of "gelijk spel". Er staan 13 wedstrijden op het formulier. Je vult die 13 wedstrijden op de gok in. Hoe groot is de kans dat je er 11 goed hebt?


5. In Voorbeeld 1 zie je hoe er sprake is van een binomiaal kansprobleem bij het werpen met vier dobbelstenen.
   1. Waarom is er in dit geval sprake van een binomiaal kansprobleem?
   2. Is dat ook het geval als je vraagt naar de kans dat er in totaal 20 ogen boven liggen?
   3. Hoe groot is de kans op één zes?
   4. Hoe groot is de kans op geen enkele zes?
   5. Stel een complete kansverdeling op voor het aantal zessen.


6. Bekijk eerst Voorbeeld 2.
   Er zijn heel veel verschillende manieren om 10 vierkeuzevragen te beantwoorden. Bij lukraak invullen heeft ieder van die manieren evenveel kans. Steeds is precies één van de vier antwoorden juist.
   1. Op hoeveel manieren kun je van die 10 vragen er precies 6 goed invullen?
   2. Welke kans heeft ieder van die manieren bij lukraak invullen?
   3. Wat is bij lukraak invullen de kans dat je van de 10 vragen er precies 6 goed invult?


7. Voor deze opgave werk je nog steeds met het voorbeeld van de 10 vierkeuzevragen die je, niet gehinderd door enige kennis, invult. Bekijk eventueel Voorbeeld 3.
   1. Bereken de kans dat je van de 10 vragen er 9 goed invult.
   2. Bereken de kans dat je van de 10 vragen er 8 goed invult.
   3. Bereken de kans dat je minstens 7 vragen goed beantwoordt.
   4. Bereken de kans dat je hoogstens 9 vragen goed beantwoordt.


8. Kijk nog eens naar de kansproblemen beschreven in opgave 4.
   Bepaal van elk van de binomiale kansproblemen de oplossing in vier decimalen nauwkeurig.
   


9. 11% van de Nederlanders is kleurenblind. Je zit in een klas met 28 medeleerlingen.
   1. Hoe groot is de kans dat er van de 28 medeleerlingen ééntje kleurenblind is?
   2. Hoe groot is de kans dat er 5 kleurenblinden in jouw klas zitten als je zelf kleurenblind bent?
   3. Hoe groot is de kans dat er 5 kleurenblinden in jouw klas zitten als je zelf niet kleurenblind bent?
   4. Hoe groot is de kans dat er van de 28 medeleerlingen hoogstens 3 kleurenblind zijn?

Verwerken

10. In een ziekenhuis staan op de kraamafdeling 10 bedjes met in elk bedje één goed toegedekte zuigeling. Ga ervan uit, dat de kans dat er een jongetje in zo’n bedje ligt even groot is als de kans dat het een meisje is.
    1. Hoe groot is de kans dat er 4 meisjes in die bedjes liggen?
    2. Maak een kansverdeling voor het aantal meisjes in de tien bedjes.
    3. Hoe groot is de kans dat je minstens 8 meisjes in de bedjes aantreft?
    4. Hoe groot is de kans dat je hoogstens 8 meisjes in de bedjes aantreft?


11. Je gooit 15 keer met een gewone dobbelsteen. Je telt het aantal keren dat er 1 boven komt.
    1. Waarom is dit een binomiaal kansprobleem?
    2. Hoe groot is de kans dat er precies 3 keer een 1 boven komt?
    3. Hoe groot is de kans dat er minder dan 3 keer een 1 boven komt?
    Je let op het totaal aantal ogen dat boven komt.
    4. Waarom is er nu geen sprake van een binomiaal kansexperiment?
    5. Hoe groot is de kans dat er 17 ogen boven komt?


12. Stel je eens voor dat 15% van alle Nederlanders contactlenzen draagt. Je staat in een winkel. Er zijn 6 klanten (uitgezonderd jezelf) en 2 verkopers. Je kent er niemand van.
    Hoe groot is de kans dat van deze 8 personen meer dan 2 contactlenzen dragen?
    

Testen

13. Vier mensen spelen het spel "Mens erger je niet". Bij dit spel mag je pas beginnen als je een zes hebt gegooid.
    1. Hoe groot is de kans dat er precies één speler in de eerste ronde mag beginnen?
    2. Hoe groot is de kans dat in de eerste ronde iedereen mag beginnen?
    Het aantal spelers dat in de eerste ronde mag beginnen wordt voorgesteld door `X`.
    3. Welke waarden kan `X` aannemen?
    4. Stel een kansverdeling op voor `X`.
    5. Bereken de kans dat er hoogstens 3 spelers de eerste ronde mogen beginnen.


14. In 2009 was ongeveer 38% van de mobiele telefoons een Nokia. In een 5 havo klas zaten dat jaar 30 leerlingen die allemaal een mobiele telefoon hebben.
    Hoe groot is de kans dat 10 van hen een Nokia hebben?