Totaalbeeld

Samenvatten

Je hebt nu het onderwerp Machtsfuncties doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

Begrippenlijst:

51: recht evenredig met een macht — machtsfunctie
52: eigenschappen van machten (rekenregels)
53: omgekeerd evenredig (met een macht) — asymptoten
54: lineair gebroken functie

Activiteitenlijst:

51: een recht evenredig verband tussen een variabele en een macht van de andere variabele herkennen — bijbehorende vergelijkingen oplossen
52: werken met de eigenschappen van machten — een formule van een machtsfunctie opstellen vanuit een tabel
53: een omgekeerd evenredig verband tussen een variabele en een (macht van de) andere variabele herkennen — asymptoten herkennen en interpreteren — bijbehorende vergelijkheden en ongelijkheden oplossen
54: lineair gebroken functies herkennen — bijbehorende vergelijkheden en ongelijkheden oplossen

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Machtsfuncties > Totaalbeeld > Achtergronden

Testen

  1. De gymnastiekdocenten van een school organiseren een prestatieloop voor de vierde klassen. Er moet een afstand van vijftien kilometer worden afgelegd. De gemiddelde snelheid voor een loper in kilometer per uur is `v`, de totale tijd t.
    1. Geef een formule die de looptijd `t` uitdrukt in de gemiddelde snelheid `v`.
    2. Hoeveel bedraagt de snelheid bij een looptijd van 100 minuten?
    Alle lopers zijn onderweg ongeveer vijf minuten tijd kwijt met het wachten bij een aantal stempelposten.
    1. Maak met dit gegeven een formule voor `t` van de vorm `t = a/v + c`.
    2. Bereken met de tweede formule de gemiddelde snelheid van een loper die in het totaal een uur en twintig minuten nodig heeft.
    3. De gemiddelde snelheid in de eerste formule is niet dezelfde gemiddelde snelheid als die in de tweede. Wat is het verschil?

  2. Zoogdieren hebben allemaal ongeveer dezelfde lichaamstemperatuur. Het verband tussen het lichaamsgewicht `G` (in grammen) en de energie `P` (in joule) die per minuut nodig is om de lichaamstemperatuur constant te houden is ongeveer zo weer te geven:

    `P = 0,017G^(3/4)`

    1. Bereken hoeveel joule per minuut een aap van 70 kilo nodig heeft om zijn lichaamstemperatuur constant te houden.
    2. Bereken welk lichaamsgewicht een zoogdier heeft dat per minuut 81 joule gebruikt om zijn lichaamstemperatuur constant te houden.
    3. Wat gebeurt er met P als het lichaamsgewicht twee keer zo groot wordt?
    Er geldt: voor een verbranding ter grootte van 350 joule is één liter zuurstof nodig.
    1. Hoeveel liter zuurstof gebruikt de aap uit a per minuut?
    2. Bereken welk lichaamsgewicht een zoogdier heeft dat per minuut 0,1 liter zuurstof gebruikt om zijn temperatuur constant te houden.

  3. Een balk heeft een vierkant grondvlak met zijde `a` en een hoogte van `h`.
    1. Druk de totale oppervlakte `Opp` van de balk uit in `a` en `h`.
    2. Druk de inhoud `I` van de balk uit in `a` en `h`.
    3. Bereken `a` als gegeven is dat `Opp = 144` en `h = 12`.
    4. Bereken `a` als gegeven is dat `I = 235` en `h = 5a`.
    5. Wat gebeurt er met de oppervlakte als alle afmetingen van de balk drie keer zo groot worden?
    6. Wat gebeurt er met de inhoud als alle afmetingen van de balk drie keer zo groot worden?

  4. Schrijf de volgende functies in de vorm `y = a + b * x^p`, waarin `a`, `b` en `p` constanten zijn.
    1. `y_1 = 1,2 * sqrt(x)`
    2. `y_2 = 200 + (0,25)/x`
    3. `y_3 = (24x^(2,4))/(6x^(1,8))`
    4. `y_4 = (4 + 3x)/x`

  5. Een kalkoen braden is lastig, omdat het enige tijd duurt voordat ook het binnenste van de kalkoen op temperatuur komt. Hoe lang dat duurt hangt af van het gewicht. Het is de kunst om de kalkoen zo lang te braden dat het binnenste net gaar is. Je kunt dat niet controleren zonder de kalkoen aan te snijden. De optimale braadtijd is daarom moeilijk vast te stellen. Gelukkig geven kookboeken vaak aanwijzingen voor de braadtijd, die afhankelijk is van het gewicht van de kalkoen. Onderzoekers hebben vastgesteld dat met de volgende formule het beste resultaat wordt verkregen:

    `t = 11g^(2/3)`

    Hierin is `g` het gewicht van de kalkoen in kilogram en `t` de tijd in minuten die nodig is om het binnenste van de kalkoen op een temperatuur van `85`°C te brengen.
    1. Bereken hoe lang het bij een kalkoen van `3` kg duurt voor het binnenste op een temperatuur van `85`°C is. Verwacht je dat een kalkoen van `6` kg daarvoor twee keer zoveel tijd nodig heeft?
    2. Als het binnenste van de kalkoen een temperatuur heeft van `85`°C duurt het nog een tijd voordat de kalkoen gaar is. Ga ervan uit dat die tijd `80` minuten is en dat die tijd afhangt van het gewicht van de kalkoen. Geef de formule voor de totale braadtijd `T` van een kalkoen afhankelijk van het gewicht. Is de totale braadtijd recht evenredig met een macht van het gewicht?
    3. Verklaar waarom het minder moeilijk is om kooktijden vast te stellen dan braadtijden. Is de kooktijd van bijvoorbeeld aardappels ook afhankelijk van het gewicht? En de totale tijd dat aardappels op het fornuis moeten staan?

  6. Los algebraïsch de volgende vergelijkingen op:
    1. `500/(v - 10) = 20`
    2. `500/v - 10 = 20`
    3. `25 - 5a^(1,2) = 10`
    4. `25 - 5/(a^(1,2)) = 10`

Toepassen

  1. Literblik

    Stel je voor dat een fabrikant zuiver cilindervormige blikken nodig heeft met een inhoud van 1 L. Om de kosten te drukken wil hij zo min mogelijk blik gebruiken. Welke afmetingen moet zo'n literblik krijgen? Lees hierover in

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Machtsfuncties > Totaalbeeld > Toepassingen

    1. Wordt bij de formule voor de oppervlakte `A` ook het deksel en de bodem van het blik meegerekend? Waaraaan zie je dat?
    2. Laat zien hoe je de formule voor `A` als functie van `r` kunt afleiden.
    3. Maak zelf de bijpassende grafiek van `A` en bepaal voor welke `r` de materiaalkosten zo klein mogelijk zijn.
    4. Voor bepaalde stoffen (bijvoorbeeld verschillende soorten olie) worden zuiver balkvormige blikken gebruikt. In verband met het makkelijk stapelen worden voor een bepaald merk olie 10-liter-blikken gebruikt waarvan lengte en breedte gelijk zijn. Bereken ook voor deze blikken de afmetingen bij een zo klein mogelijke oppervlakte aan blik.

  2. Meeh-coëfficiënt

    Er bestaan in de biologie en de fysiologie allerlei verbanden tussen maten van dieren (en maten van mensen). Een bekend voorbeeld is dat tussen huidoppervlakte en lichaamsgewicht. De fysioloog Karl Meeh vond dit verband als eerst, maar je kunt het ook zelf afleiden. Lees hierover

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Machtsfuncties > Totaalbeeld > Toepassingen

    In de tekst wordt de Meeh-coëfficiënt van een massieve houten kubus afgeleid. De soortelijke massa van dat hout is 5 gram per cm3.
    1. Leg uit waarom de Meeh-coëfficiënt van de kubus ongeveer 206 is.
    2. Bepaal zelf de Meeh-coëfficiënt van een massieve bol met straal `r` van deze houtsoort.
      De inhoud van een bol is `I = 4/3 pi r^3` en de oppervlakte is `H = 4pi r^2`.
    3. Bepaal ook de Meeh-coëfficiënt van een massieve cilinder van deze houtsoort. Ga er van uit dat de cilinder even hoog is als zijn diameter is.
    4. Hoe kun je dit gebruiken om de Meeh-coëfficiënt van een bepaalde diersoort te schatten?

Examenopgaven

  1. Diersoorten

    Het lijkt aannemelijk dat er een verband bestaat tussen de oppervlakte van een gebied en het aantal verschillende diersoorten dat in dat gebied voorkomt. Een theorie hierover stelt dat het aantal verschillende diersoorten op een eiland in een bepaalde klimaatzone alleen afhankelijk is van de oppervlakte van het eiland. In deze opgave kijken we naar de verschillende soorten reptielen op eilanden in het Caraïbisch gebied.
    Onderzoekers telden op vele eilanden het aantal verschillende soorten reptielen (`S`). In de volgende figuur zijn de gegevens van enkele eilanden weergegeven.



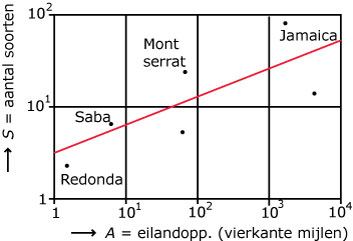
    Volgens de theorie is het verband tussen de oppervlakte `A` ven een eiland (in vierkante mijlen) en het aantal soorten reptielen (`S`) op dat eilandente beschrijven met de formule `S = 3 * A^(0,30)`.
    De lijn in de bovenstaande figuur is de grafiek die bij deze formule behoort.
    1. Op het eiland Jamaica zijn meer soorten reptielen aangetroffen dan op grond van de theorie (de formule) verwacht mag worden. Hoeveel soorten reptielen zou een even groot eiland volgens de theorie hebben? Licht je antwoord toe.
    2. Binnen de theorie geldt als ruwe regel: "Bij een 10 keer zo groot eiland vinden we 2 keer zoveel diersoorten." Laat zien dat dit uit de formule volgt.
    Op een groot eiland worden veel verschillende soorten reptielen met uitsterven bedreigd. Men wil maatregelen nemen om de natuur te beschermen. Daarbij moet er een keuze worden gemaakt uit twee mogelijkheden:
    1. Oprichting van 1 groot natuurreservaat met een oppervlakte van 400 vierkante mijlen.
    2. Oprichting van 2 kleinere reservaten, elk met een oppervlakte van 200 vierkante mijlen.
    Dergelijke natuurreservaten liggen geïsoleerd in de bewoonde wereld en kunnen als 'eilanden' beschouwd worden. Voor het schatten van het aantal soorten reptielen dat in zo’n reservaat zal voorkomen kan de formule `S = 3* A^(0,30)` gebruikt worden. Of voor 1 of 2 gekozen wordt, is mede afhankelijk van het aantal soorten dat de twee kleinere reservaten gemeen zullen hebben. Men neemt aan dat er 8 soorten reptielen zijn die zowel in het éne als het andere kleine reservaat zullen voorkomen. Men wil de mogelijkheden kiezen waarbij in totaal zoveel mogelijk verschillende soorten reptielen zullen voorkomen.
    1. Welke van de twee mogelijkheden zal men kiezen? Licht je antwoord toe.

    (bron: examen wiskunde A havo 1993, eerste tijdvak)