Lineair gebroken functies

Antwoorden bij de opgaven

1. 1. `150/100 = 1,5` uur rijden plus een half uur pauze is in totaal 2 uur.
   2. Eerst het half uur pauze er af. Dan `150/s = 2`, dus snelheid `= 75` km/h.
   3. `t = 150/(text(gem.snelheid)) + 0,5`
   4. `text(gemiddelde snelheid) = 150/t + 0,5`
   5. `t = 150/v + 0,5`
   6. `v = 150/(t - 0,5)`
   7. `t > 0,5` en `v > 0`.
2. 1. `k = 0,12 + 25/a`
   2. Vanwege de vaste kosten van € 0,12 per folder wordt de prijs per folder niet gehalveerd als het aantal folders wordt verdubbeld.
   3. Horizontale asymptoot: `k = 0,12`.
      Verticale asymptoot: `a = 0`.
   4. `k = 0,12 + 25/a = 0,15` geeft `25/a = 0,03` en dus `a = 25/(0,03) ~~ 833,3`. Dus vanaf 834 folders komt de prijs niet boven de 15 cent per stuk.
3. 1. -
   2. Bij snelheden vanaf de 30 km/h t/m 150 km/h waarschijnlijk.
   3. `4,4 + (196,0)/v = 6` geeft `(196,0)/v = 1,6` en dus `v = 122,5` km/uur. Dus voor snelheden groter dan 122,5 km/uur.
   4. `4,4 + (196,0)/v = 5,4` geeft `(196,0)/v = 1,0` en dus `v = 196,0` km/uur. Dus voor snelheden groter dan 196,0 km/uur. Maar of de formule dan nog geldig is...
4. 1. `400/v = 80` geeft `v = 5`.
   2. `20/(a - 10) = 16` geeft `a - 10 = 1,25` en dus `a = 11,25`.
5. 1. Je betaalt toch de vaste kosten en de telefoonkosten.
   2. Vaste kosten zijn € 2,50, dus `k = 2,50/a` met `k` de kosten in de eerste 8 uren en `a` het aantal uren.
   3. Na 8 uur betaal je € 1,25 voor elk uur plus een deel van de vaste kosten. Het deel van de vaste kosten dat je nog betaalt is 2,5 euro gedeeld door het extra aantal uren `a - 8`.
   4. `1,25 + (2,5)/(a - 8) = 1,30` geeft `(2,5)/(a - 8) = 0,05` en dus `a - 8 = 50` en `a = 58`. Vang 58 uur per maand zijn de kosten lager dan € 1,30.
6. 1. Neem bijvoorbeeld Xmin = 1, Xmax = 5, Ymin = 0 en Ymax = 50.
   2. Bij de eerste, want bij de tweede zit de prijs meestal in de buurt van de 25 euro.
   3. De tweede functie, dus `a_2`.
   4. De horizontale asymptoot is `y = 0`, dus de ondergrens is 0.
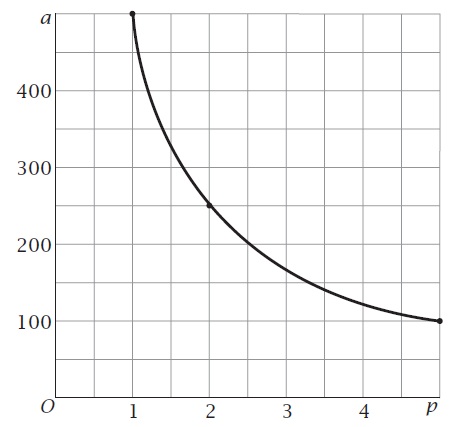
   5. Volgens de eerste formule: `500/p = 50`, dus `p = 10` en dus is de prijs € 10,= per kilo.
      Volgens de tweede formule: `400/p + 25 = 50`, dus `400/p = 25` en `p = 8` en dus is de prijs € 8,= per kilo.
7. 
   1. `p = 10`, dus `k = 195/10 = 19,5` kg. Vaste verkoop 10 kg, dus totale verkoop 29,5 kg.
   2. `k = 195/p + 10`, dus `c = 10`.
   3. De GR geeft 13 euro/kg.
   4. `195/p + 10 = 25` geeft `195/p = 15` en dus `p = 13`, dus 13 euro/kg.
   5. Nieuwe formule: `k = 195/p + 12,5`.
8. 1. `p = (2,25)/(0,45) = 5`.
   2. `k = 300/(0,20) = 15`.
   3. `k + 12 = 1200/48 = 25` dus `k = 13`.
9. 1. Ja, hoe groter `b` hoe kleiner `50/b`, dus `p` wordt kleiner.
   2. `p = 50/200 + 15 = 15,25`%.
   3. 15%.
   4. `50/b = 75` geeft `b = 2/3`. Dus `b ~~ 0,67` miljoen euro; de formule geldt hier niet.
10. 1. `TK = 20000 + 160q` bij een productie van `q` exemplaren, dus `GTK = TK/q = 20000/q + 160`.
    2. `TO = pq = 210q`. Winst als `TO > TK`, dus als `210q > 20000 + 160q` en `50q > 20000` zodat `q > 400`.
11. 1. GR: Y1=130/X+3,Y2=130/X+7,Y3=130/X+10 en Y4=130/X+1 met venster: `-1 <= X <= 20` en `-1 <= Y <= 50`.
    2. De grafiek schuift nog verder naar boven.
    3. `130/15 + c = 20` geeft `8 2/3 + c = 20` en dus `c = 11 1/3`.
12. 1. `T - 2 = 300/50 = 6` en dus `T = 8`.
    2. `300/T = 50` geeft `T = 6`.