Omgekeerd evenredig

Inleiding

Ga je met de auto van het centrum van Apeldoorn naar dat van Deventer, dan geeft de ANWB-routeplanner aan dat je een stuk van 16 km op de snelweg moet rijden. Hoe sneller je rijdt, hoe korter je over die 16 km doet. De tijd die je nodig hebt is omgekeerd evenredig met de snelheid.

Je leert nu:

• wat het begrip omgekeerd evenredig inhoudt;
• hoe de formule er uitziet als de éne variabele omgekeerd evenredig is met (een macht van) de andere;
• bij grootheden die omgekeerd evenredig zijn (met een bepaalde macht) tabellen maken, grafieken tekenen.

Je kunt al:

• werken met machten en machtsfuncties;
• werken met breuken.

Verkennen

Bekijk het verhaal van de route van het centrum van Apeldoorn naar dat van Deventer bij de Inleiding.

> Je mag maximaal 120 km/h rijden op de snelweg. Hoeveel minuten ben je dan onderweg?
> Het is druk dus je rijdt (gemiddeld) 80 km/h. Hoeveel minuten ben je onderweg?
> Welke formule kun je opstellen voor de reistijd t (in min.) als functie van de snelheid v (in km/h)?

Uitleg

Van Apeldoorn naar Deventer is met de auto 16 km over de snelweg. Hoe sneller je rijdt, hoe korter je over die 16 km doet. De tijd die je nodig hebt is omgekeerd evenredig met de snelheid: rijd je 2 keer zo snel, dan heb je de helft van de reistijd nodig.

• Je mag maximaal 120 km/h rijden op de snelweg. Je bent dan $\frac{16}{120}\cdot 60$ = 8 minuten onderweg.
• In de drukte kun je (gemiddeld) maar 60 km/h rijden. Dan ben je $\frac{16}{60}\cdot 60$ = 16 minuten onderweg.

Je ziet dat je de reistijd t in minuten kunt berekenen door de afstand van 16 km te delen door de snelheid v (in km/h) en met 60 te vermenigvuldigen:
t = $\frac{16}{v}\cdot 60$ = $\frac{960}{v}$

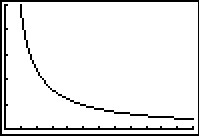De grafiek van zo'n omgekeerd evenredig verband zie je hiernaast.
Voor snelheden dicht bij 0 wordt de reistijd heel erg groot.
Voor hele grote snelheden wordt de reistijd vrijwel 0.
De grafiek heeft daarom twee asymptoten.

‡

Opgaven

1. Bekijk in de Uitleg de reistijd van Apeldoorn naar Deventer afhankelijk van de gemiddelde snelheid.
   Iemand uit Apeldoorn bezoekt regelmatig familie in Rotterdam. De afstand tussen Apeldoorn en Rotterdam is ongeveer 150 kilometer.
   1. Hoe lang duurt de rit als er gemiddeld 100 kilometer per uur wordt gereden?
   2. Met welke snelheid is er gemiddeld gereden als de rit twee uur duurt?
   3. Hoe bereken je de tijdsduur als je de gemiddelde snelheid weet?
   4. Hoe bereken je de gemiddelde snelheid als je de tijdsduur weet? Neem voor de tijdsduur de variabele `t` en voor de gemiddelde snelheid de variabele `v`.
   5. Geef een formule voor `t` als functie van `v`.
   6. Geef ook een formule die `v` uitdrukt in `t`.
   7. Voor welke waarden van `v` is deze formule volgens jou bruikbaar?

Theorie

Twee variabelen x en y zijn omgekeerd evenredig als het vermenigvuldigen van x met een getal k tot gevolg heeft dat y met $\frac{1}{k}$ wordt vermenigvuldigd. Bijvoorbeeld: wordt x twee keer zo groot, dan wordt y een half keer zo groot.
Bij een omgekeerd evenredig verband hoort een formule van de vorm
y = $\frac{\mathrm{c}}{x}$  met c constant.
Je kunt die formule ook schrijven als x · y = c.

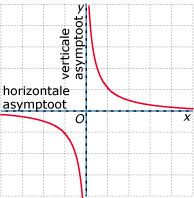
De grafiek van zo'n omgekeerd evenredig verband is een hyperbool met twee asymptoten:

• de horizontale asymptoot y = 0;
• de verticale asymptoot x = 0.

In het algemeen kan y ook omgekeerd evenredig zijn met een macht van x. Je krijgt dan een formule van de vorm
$y=\frac{c}{x^p}$  met c en p constant.
Door in de applet de p te variëren kun je zien hoe de grafieken van dergelijke functies er uit zien. Bij gehele getallen voor p kan x zowel positief als negatief zijn; voor andere waarden van p kan dit niet. In de praktijk komen negatieve waarden van x bij omgekeerd evenredigheid niet voor.

‡

Voorbeeld 1

Als een rechthoekig tafelblad een oppervlakte van 1 m² heeft, kunnen lengte l en breedte b nog variëren. Laat zien dat l en b omgekeerd evenredig zijn en stel een passende formule op met l en b in cm.

Antwoord

Voor de rechthoek geldt: l · b = oppervlakte = 10000 cm².
Dit kun je schrijven als: l = $\frac{10000}{b}$.

Bij b = 100 hoort l = 10000/100 = 100.
Bij b = 200 hoort l = 10000/200 = 50.
Wordt b twee keer zo groot, dan wordt l gehalveerd. En dit kun je gemakkelijk ook voor andere waarden nagaan. Inderdaad zijn l en b omgekeerd evenredig.

‡

Voorbeeld 2

De lichtsterkte S (in Watt/m²) van een lamp is omgekeerd evenredig met het kwadraat van de afstand r (in m) tot de lichtbron. Stel een formule op voor de lichtsterkte van een straatlantaarn met een vermogen van 1000 Watt.
Zo'n straatlantaarn is 5 m hoog. Hoeveel zou het vermogen moeten bedragen als die lamp op 4 m hoogte zou hangen en de lichtsterkte op straat recht onder de lamp gelijk moet blijven?

Antwoord

Een lamp met een vermogen van 1000 Watt levert op 1 m afstand een lichtsterkte van 1000 W/m².
De formule heeft de vorm S = $\frac{c}{r^2}$, dat wordt dus S = $\frac{1000}{r^2}$.

De straatlantaarn van 1000 W die op 5 m hoogte hangt levert recht onder de lamp een lichtsterkte van $\frac{1000}{5^2}$ = 40 W/m².
De straatlantaarn van c W die op 4 m hoogte hangt levert recht onder de lamp een lichtsterkte van $\frac{c}{4^2}$ = 40 W/m².

Dit betekent: c = 40 · 16 = 640 W.

‡

Voorbeeld 3

Los op: $\frac{6}{x^{\mathrm{1,5}}}$ = 3.

Antwoord

Dit kun je op twee manieren aanpakken.

Eerste manier:

  $\frac{6}{x^{\mathrm{1,5}}}$ = 3            _{lijkt op $\frac{6}{2}$ = 3}
  x^1,5 = $\frac{6}{3}$ = 2      _{omgekeerde macht gebruiken}
      x = 2^{$\frac{1}{\mathrm{1,5}}$}  ≈ 1,587

Tweede manier:

     $\frac{6}{x^{\mathrm{1,5}}}$ = 3           _{functie als machtsfunctie schrijven}
  6 · x^–1,5 = 3        _{beide zijden delen door 6}
  x^–1,5 = $\frac{3}{6}$ = 0,5     _{omgekeerde macht gebruiken}
   x = 0,5^{$\frac{1}{-\mathrm{1,5}}$}  ≈ 1,587

‡

Opgaven

2. Bekijk Voorbeeld 1. Lengte `l` en breedte `b` van een rechthoek met een vaste oppervlakte van 1 m² zijn omgekeerd evenredig.
   1. Welke drie formules kun je opschrijven voor het verband tussen `l` en `b` als beide in cm zijn?
   2. Teken de grafiek van `l` als functie van `b` op je grafische rekenmachine.
      Welke asymptoten heeft deze grafiek?
   3. Laat met behulp van de formule uit b zien dat `l` wordt gehalveerd als `b` wordt verdubbeld.
   4. Als `b` tien keer zo groot wordt, hoeveel keer zo groot wordt `l` dan?
   5. Als `b` ééntiende keer zo groot wordt, hoeveel keer zo groot wordt `l` dan?


3. In Voorbeeld 2 zie je dat de lichtsterkte S (in Watt/m²) van een lamp omgekeerd evenredig is met het kwadraat van de afstand r (in m) tot de lichtbron.
   1. Waarom betekent dit in wiskundetaal `S = c/(r^2)`?
   2. Leg uit waarom voor een lamp met een vermogen van 1000 Watt geldt `c = 1000`.
   3. In een straatlantaarn zit een lamp met een vermogen van 1000 Watt op 4,5 m hoogte. Hoeveel bedraagt te lichtsterkte op de grond, recht onder de lamp?
   4. Welke asymptoten heeft de grafiek van `S = 1000/(r^2)`?
   5. In een straatlantaarn zit een lamp van 1000 Watt. De lichtsterkte op de grond recht onder de lamp bedraagt 50 W/m². Hoe hoog hangt de lamp?


4. Gegeven is de formule `y = 6/(x^(1,5))`.
   1. Maak de grafiek bij deze formule.
   2. Maak ook de grafiek bij `y = 6 * x^(-1,5)`. Wat valt je op? Verklaar dit.
   3. Verklaar de uitspraak: omgekeerd evenredig met een macht van `x` is hetzelfde als recht evenredig met de tegengestelde macht van `x`.
   4. Welke asymptoten heeft deze grafiek?
   In Voorbeeld 3 zie je hoe `6/(x^(1,5)) = 3` op twee manieren kan worden opgelost.
   5. Los nu zelf `6/(x^(1,5)) = 12` op deze twee manieren op.


5. Schrijf de volgende functies in de vorm `y = ax^b`. Doe dit nu zelf bij de volgende functies:
   1. `y_1 = 6/(2x^4)`
   2. `y_2 = 1/(3x^6)`
   3. `y_3 = (12x^8)/(4x^10)`
   4. `y_4 = 4/(sqrt(x))`

Verwerken

6. In een groot winkelbedrijf wordt onderzocht hoe de tomatenverkoop afhangt van de prijs. Iemand beweert dat de volgende formule geldt:

   `a = 500/p`

   Hierin is `a` de verkoop per dag in kilogrammen en `p` de prijs per kilogram in euro.
   1. Maak een grafiek waaruit je de verkoop kunt aflezen voor prijzen tussen de € 1,= en € 5,= per kilogram.
   2. Iemand zegt: "Een verdubbeling van de prijs zorgt voor een halvering van de verkoop". Klopt dat?
   3. Klopt deze bewering met de formule: “Als de prijs vijf keer zo hoog wordt, wordt de verkoop vijf keer zo klein.”?
   4. Geef twee andere formules voor hetzelfde verband tussen `a` en `p`.
   5. In het bedrijf heeft men een voorraad van 300 kg tomaten. Die is niet lang meer houdbaar en men wil er binnen een dag vanaf. Wat mag de prijs maximaal zijn volgens de formule?
   Een formule zoals `a = 500/p` is meestal slechts bruikbaar op een beperkt gebied. Dat kun je zien als je voor `p` extreme gevallen neemt.
   5. Wat zal volgens de formule de verkoop zijn bij een prijs van € 0,01? En bij een prijs van € 100,=? Zal dit in werkelijkheid ook zo zijn?
   6. Geef aan voor welke prijzen de formule volgens jou bruikbaar zou kunnen zijn.


7. Een kaasboer houdt bij hoeveel kilo geraspte kaas hij per week verkoopt. Het blijkt dat de hoeveelheid `k` (in kg) die hij verkoopt omgekeerd evenredig is met de prijs `p` per kilo. Bij een prijs van € 13,= per kilo verkoopt hij vijftien kilogram geraspte kaas.
   1. Bereken `p * k` met behulp van de gegevens en geef vervolgens een formule die `k` uitdrukt in `p`.
   2. Bereken het aantal verkochte kilo’s als de prijs € 10,= per kilogram is.


8. Schrijf de volgende functies in de vorm `y = a * x^b`.
   1. `y_1 = 4/(8x^3)`
   2. `y_2 = (4x^2)/(8x^3)`
   3. `y_3 = (-3)/(sqrt(x))`


9. Bekijk de grafiek die het verband tussen de snelheid en de tijd weergeeft voor iemand die van Utrecht naar Den Bosch reist. De (gemiddelde) snelheid `v` (in km/uur) is omgekeerd evenredig met de tijd `t` (in uur).
   1. Een wandelaar heeft een gemiddelde snelheid van vijf kilometer per uur. Hoe lang doet hij over de afstand Utrecht - Den Bosch?
   2. Een fietser doet vijf uur over deze afstand. Wat is zijn gemiddelde snelheid?
   3. Bereken uit je antwoorden bij a en b het product van de tijd en de snelheid. Stel een formule op die bij de grafiek past.
   4. De trein van Utrecht naar Den Bosch doet er ongeveer 25 minuten over. Hoeveel kilometer per uur rijdt de trein?


10. In de onderstaande tabel zie je voor verschillende rentepercentages de verdubbelingstijd: de tijd die nodig is om het kapitaal te laten verdubbelen.
    
    

    rentepercentage per jaar	3,0	3,5	4,0	4,5	5,0
    verdubbelingstijd in jaren	23,4	20,1	17,7	15,7	14,2

    
    
    1. Laat met berekeningen zien dat tussen het rentepercentage en de verdubbelingstijd ongeveer een omgekeerd evenredig verband bestaat.
    2. Druk de verdubbelingstijd `T` uit in het rentepercentage `r`.
    3. Bereken met behulp van de formule uit b de verdubbelingstijd bij een rentepercentage van 3,75.
    4. Bereken de verdubbelingstijd uit c door met je grafische rekenmachine deze vergelijking op te lossen: `(1,0375)^T = 2`.
    5. Maak c en d nog eens, maar nu voor een rentepercentage van 12.
    6. Welke conclusie kun je uit de antwoorden bij e trekken over de geldigheid van de formule uit b?

Toetsen

11. Dat wijnglazen groter zijn dan portglazen is niet toevallig. Voor de inhoud `I` (in cm³) van een glas en het alcoholpercentage `p` van de drank die erin hoort geldt namelijk ongeveer deze formule: `p * I = 1200`.
    1. Leid uit het bovenstaande af of wijn een hoger of lager alcoholpercentage heeft dan port.
    2. Gewoon bier heeft een alcoholpercentage van ongeveer 5. Bereken de inhoud van een bierglas.
    3. Een jeneverglas heeft een inhoud van 35 cm³. Wat is het alcoholpercentage van jenever?
    4. Geef een formule voor `I` als functie van `p`.
    5. Alcoholarm bier heeft een percentage van 2. Is de formule nog bruikbaar voor alcoholarm bier? Tussen welke grenzen kun je `p` ongeveer laten variëren?


12. Schrijf de volgende functies in de vorm `y = a * x^b`.
    1. `y_1 = 1/(2x)`
    2. `y_2 = 2/(x^3)`
    3. `y_3 = 1/(2sqrt(x))`
    4. `y_4 = (3x)/(4x^2 sqrt(x))`


13. Plaatjes in bijvoorbeeld boeken, tijdschriften en kranten bestaan meestal uit een groot aantal stipjes (of streepjes). Hoe meer stipjes per cm², hoe duidelijker het plaatje. In de tabel zie je hoe bij het aantal stippen per cm² de oppervlakte per stip varieert.
    
    

    aantal stippen per cm2	10	25	50	100	150	200
    oppervlakte van één stip in cm2	0,090	0,036	0,018	0,009	0,006	0,0045

    
    
    1. Toon aan dat het verband tussen het aantal stippen `a` per cm² en de oppervlakte per stip `A` (in cm²) omgekeerd evenredig is.
    2. Geef een formule die `A` uitdrukt in `a`.
    3. Bij hoeveel stippen per cm² is de oppervlakte per stip kleiner dan 0,001 cm²?