Omgekeerd evenredig

Antwoorden bij de opgaven

1. 1. `150/100 = 1,5` uur.
   2. `150/s = 2`, dus snelheid= 75 km/h.
   3. `t = 150/(text(gem.snelheid))`
   4. `text(gemiddelde snelheid) = 150/t`
   5. `t = 150/v`
   6. `v = 150/t`
   7. `t > 0` en `v > 0`.
2. 1. `l * b = 10000`, `l = 10000/b` en `b = 10000/l`.
   2. De horizontale asymptoot is `l = 0` en de verticale asymptoot is `b = 0`.
   3. Als je `b` vervangt door `2b` krijg je `l = 10000/(2b) = 1/2 * 10000/b`.
   4. Eéntiende keer.
   5. Tien keer.
3. 1. `S` is evenredig met het omgekeerde van `r^2`, dus een veelvoud van `1/(r^2)`. Dat betekent: `S = c * 1/(r^2) = c/(r^2)`.
   2. Bij een vermogen van 1000 Watt heb je op een afstand van 1 m ook precies 1000 Watt per m².
      Neem je `r = 1` en `S = 1000` en vul je dit in `S = c/(r^2)` in dan wordt `c = 1000`.
   3. `S = 1000/(4,5^2) ~~ 49` W/m².
   4. Verticale asymptoot `r = 0` en horizontale asymptoot `S = 0`.
   5. `1000/(r^2) = 50` geeft `r = sqrt(20) ~~ 4,47` m.
4. 1. -
   2. Je krijgt twee dezelfde grafieken, want `6/(x^(1,5)) = 6 * 1/(x^(1,5)) = 6 * x^(-1,5)`.
   3. Omgekeerd even redig met `x^b` is recht evenredig met `1/(x^b) = x^(-b)`.
   4. Verticale asymptoot `x = 0` en horizontale asymptoot `y = 0`.
   5. Op beide manieren vind je `x ~~ 0,63`.
5. 1. `y_1 = 3x^(-4)`
   2. `y_2 = 1/3 x^(-6)`
   3. `y_3 = 3x^(-2)`
   4. `y_4 = 4x^(-0,5)`.
6. 
   1. Zie figuur.
   2. De bewering is waar.
   3. De bewering is waar.
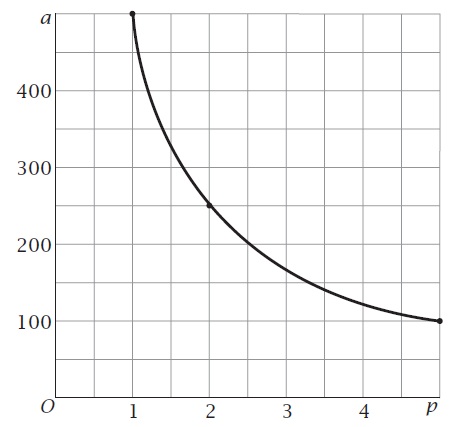
   4. `a = 500/p` en `a * p = 500`.
7. 1. `p = 13` en `k = 15`, dus `p * k = 195` en `k = 195/p`.
   2. `p = 10`, dus `k = 195/10 = 19,5` kg.
8. 1. `y_1 = 1/2 x^(-3)`
   2. `y_2 = 1/2 x^(-1)`
   3. `y_3 = -3 x^(-1//2)`
9. 1. Aflezen: ongeveer 10 uur.
   2. Ongeveer 10 km/h.
   3. `t * v = 50` dus `t = 50/v`
   4. `t = 25` min `= 25/50` uur `= 5/12` uur, dus `v = 12/5 * 50 = 120` km/h.
10. 1. `3 * 23,4 = 70,2`; `3,5 * 20,1 = 70,35`; `4 * 17,7 = 70,8`; `4,5 * 15,7 = 70,65`; `5 * 14,2 = 71,0`
    2. `r * T ~~ 70,6`, dus `T ~~ (70,6)/r`.
    3. `r = 3,75`, dus `T ~~ (70,6)/(3,75) ~~ 18,828`.
    4. Je vindt ook zo `T ~~ 18,828`.
    5. `T ~~ (70,6)/12 ~~ 5,88` en `1,12^T = 2` geeft `T ~~ 6,12`.
    6. De formule klopt kennelijk niet meer voor grotere percentages.
11. 1. `I = 1200/p`, dus als `p` groter wordt, wordt `I` kleiner. Dus kleinste inhoud heeft grootste percentage. `I_(text(wijn)) > I_(text(port))`, dus het alcoholpercentage van port is hoger dan dat van wijn.
    2. `p = 5`, dus `I_(text(bier)) = 1200/5 = 240` cm³.
    3. `I_(text(jenever)) = 35` cm³, dus `p = 1200/35 = 34,3`%.
    4. `p = 2`, dus `I = 1200/2 = 600` cm³ en dat is meer dan een halve liter. De formule is niet bruikbaar.
12. 1. `y_1 = 1/2 x^(-1)`
    2. `y_2 = 2x^(-3)`
    3. `y_3 = 1/2 x^(-1)`
    4. `y_4 = 3/4 x^(-1,5)`
13. 1. `a * A = 0,9`
    2. `A = (0,9)/a`
    3. `A < 0,001` geeft `a > 900`.