
Werken met machten

Inleiding
In een vlak landschap wordt het verband tussen de kijkafstand a (in m) en de hoogte h (in m) gegeven door de formule `a = 3573 * h^(1/2)`.
Om vanuit een gegeven waarde voor a de bijbehorende h te berekenen, gebruik je de omgekeerde macht. In dit geval is dat "kwadrateren", net als bij het terugrekenen vanuit wortels. Hier is sprake van een rekenregel voor machten en wortels...
Je leert nu:
- systematisch werken met rekenregels voor machten;
- machten met gebroken exponent omzetten in wortels en omgekeerd.
Je kunt al:
- werken met machten met gehele exponenten;
- werken met exponentiële vergelijkingen.
Verkennen
Bekijk het verhaal van de kijkafstand bij de Inleiding.
> Waarom is 2 de omgekeerde macht van `1/2`?
> Hoe kun je `(sqrt(h)^(1//2))` eenvoudiger schrijven?
> Wat kun je zeggen van `sqrt(h)` en `h^(1//2)`?
> Hoe kun je dit met de grafische rekenmachine controleren?
> Kun je nu een algemene eigenschap van machten en wortels bedenken?
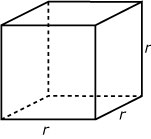
Uitleg
De inhoud van een kubus met ribben van lengte `r` is: `I = r * r * r = r^3`.
Om r uit te rekenen als gegeven is dat I = 250, kun je op twee manieren te werk gaan:
- Je neemt de omgekeerde macht: r = .
- Je rekent terug m.b.v. de derdemachts wortel: r = .
Ga na, dat je in beide gevallen dezelfde uitkomst krijgt.
Kennelijk is = .
Dit is een voorbeeld van een algemene eigenschap van machten: .
Zo zijn er meer eigenschappen van machten. Een aantal ervan ken je wel...
‡
Opgaven
- Bestudeer in de Uitleg de formule voor de inhoud van de kubus.
- Bereken de ribbe van een kubus waarvan de inhoud `125` cm3 is.
- Ga na, dat `(125)^(1//3) = root[3](125)`.
- Bereken de ribben van een kubus met een inhoud van `500` cm3.
- Ga na, dat `(500)^(1//3) = root[3](500)`.
- Ook het verband tussen de ribbe `r` en de oppervlakte `A` van een kubus is een machtsverband. De bijbehorende formule is: `A = 6 r^2`.
- Bereken de ribbe van een kubus met een oppervlakte van `216` cm2.
- Ga na, dat `(36)^(1//2) = sqrt(36)`.
- Bereken de ribbe van een kubus met een oppervlakte van `300` cm2.
- Ga na, dat `(50)^(1//2) = sqrt(50)`.
Theorie
Voor elke x en voor willekeurige reële getallen a en b gelden de volgende eigenschappen van machten en exponenten:
- xa – b = mits x ≠ 0
- mits x > 0 en a > 0.
Je kunt deze eigenschappen opvatten als rekenregels.
‡
Voorbeeld 1
Neem aan dat x ≠ 0. Laat zien, dat:
- x3 · x5 = x · x · x · x · x · x · x · x = x8
- =
= x2
- (x5)3 = x5 · x5 · x5 = x15
- , want en
‡
Voorbeeld 2
Met behulp van de rekenregels voor machten kun je allerlei functies opeens als machtsfunctie schrijven. Dat is nuttig omdat je dan gemakkelijk iets over hun eigenschappen kunt zeggen en kunt terugrekenen.
Schrijf de volgende functies als machtsfunctie.
- y2 = 15x = 15 · x1 · = 15x1,5
- y3 = 5 = 5 · = 5x
- y4 = = 6 · · x–2 = 6x–1,5
‡
| soort |
m (kg) |
Z (L) |
| muis |
0,20 |
0,19 |
| rat |
1,10 |
0,75 |
| kat |
5,80 |
2,62 |
| hond |
11,5 |
4,38 |
| mens |
76,1 |
18,0 |
| paard |
605,0 |
85,4 |
Voorbeeld 3
De Amerikaanse veearts en onderzoeker Max Kleiber ontdekte in 1932 dat het zuurstofverbruik Z (in L/uur) van verschillende soorten zoogdieren recht evenredig is met een macht van de massa m (in kg). In de tabel vind je enkele bijpassende gegevens. Stel een formule op voor Z afhankelijk van m.
Antwoord
Deze machtsfunctie heeft de vorm Z = c · mp, waarin c en p nog te berekenen zijn.
Je hebt daartoe genoeg aan de gegevens van twee diersoorten, bijvoorbeeld:
- paard: Z = 85,4 en m = 605,0 geeft: 85,4 = c · 605,0p
- muis: Z = 0,19 en m = 0,20 geeft: 0,19 = c · 0,20p
Met de balansmethode vind je dan: en dus 449,47 ≈ 3025p.
Zo'n exponentiële vergelijking los je met de GR op: p ≈ 0,76.
En nu vind je door invullen ook c ≈ 0,66.
Het resultaat komt dicht bij de door Kleiber gevonden formule Z = 0,7 · m0,75.
‡
Opgaven
-
Bekijk de rekenregels voor machten in de Theorie. Met behulp van grafieken kun je ze voor bijzondere gevallen controleren.
-
Bekijk de uitdrukking `x^2 * x^3`. Is dit nu gelijk aan `x^6` of aan `x^5`?
Vind het juiste antwoord door de grafieken van `y_1 = x^2 * x^3`, `y_2 = x^6` en `y_3 = x^5` te vergelijken.
-
Bekijk de uitdrukking `x^5 // x^3`. Is dit nu gelijk aan `x^(5//3)` of `x^2`?
Vind het juiste antwoord door de grafieken van `y_1 = x^5 // x^3`, `y_2 = x^(5//3)` en `y_3 = x^2` te vergelijken.
-
Zoek op deze manier zelf uit of `(x^2)^3` gelijk is aan `x^5` of `x^6`.
-
Bekijk de grafiek van `y = x^0`. Verklaar waarom die grafiek er zo uitziet.
-
Je kunt `x^3 // x^5` schrijven als `x^(-2)`, maar ook als `1 // x^2`. Leg dat uit.
Welke rekenregel voor machten volgt hier uit?
-
Waarom is het van belang dat `x != 0` bij de meeste rekenregels? Bij welke is dat niet belangrijk?
-
Bekijk de grafieken van `y_1 = sqrt(x)` en `y_2 = x^(0,5)`.
-
Wat valt je op? Met welke rekenregel uit de Theorie heeft dit te maken?
-
Laat zien dat `xsqrt(x) = x^(1,5)`.
-
Schrijf `y = x^2 root[3](x)` als machtsfunctie, dus in de vorm `y = x^b`.
-
Bekijk Voorbeeld 1. Laat zien dat
- `x^2 * 4x^3 = 4x^5`
- `(3x)^2 * 4x = 36x^3`
- `(6x^8)/((2x^2)^2) = 1,5x^4`
- `4xsqrt(x) * 3x^2 = 12x^(2,5)`
- `(12x^5)/(3x^7) = 4x^(-2)`
- `4(root[4](x))^6 = 4x^(1,5)`
-
In Voorbeeld 2 zie je hoe bepaalde functies kunnen worden geschreven als machtsfunctie, dus in de vorm `y = ax^b`.
Doe dit nu zelf bij de volgende functies:
- `y_1 = 2sqrt(x)`
- `y_2 = (300x^2)/(2x^(1,6))`
- `y_3 = 1,3x^3 sqrt(x)`
- `y_4 = (5x^(0,2))/(sqrt(x))`
-
Er bestaat een verband tussen het zuurstofverbruik `Z` en de lichaamsmassa `m` bij zoogdieren.
In Voorbeeld 3 kun je nalezen hoe daarvoor een formule kan worden opgesteld. Daarbij worden de gegevens van de muis en het paard gebruikt.
-
Stel nu zelf een passende formule op uitgaande van de gegevens van rat en mens.
-
Kom je ook dan in de buurt van de formule die Kleiber heeft gevonden?
-
Gebruik nu de formule van Kleiber. Van bepaald type koe is de lichaamsmassa 12 keer zo groot dan van de mens. Hoeveel keer zo groot is het zuurstofverbruik?
-
Een bepaalde diersoort heeft een zuurstofverbruik van ongeveer 30 L/uur. Hoeveel bedraagt de lichaamsmassa ongeveer?
Verwerken
-
Een aantal dozen heeft allemaal een vierkant grondvlak en een vierkant bovenvlak en rechthoekige zijvlakken. Het grondvlak heeft zijden van `r` cm en de inhoud van de dozen is `I` cm3.
- Laat zien dat `I` recht evenredig is met `r^3`.
- Laat zien dat de doos waarop deze formule van toepassing is, twee keer zo hoog is als breed is.
- Neem nog eens de formule uit b. Laat zien, dat de inhoud van de doos 8 keer zo groot wordt als de zijde van het grondvlak met 2 wordt vermenigvuldigd.
- Voor één van deze dozen geldt `r = 25` en `I = 23437,5`. Hoe hoog is deze doos?
Als je de inhoud van zo’n doos weet en je wilt de zijde van het grondvlak berekenen, dan kun je deze formule gebruiken: `r = (I/c)^(1//3)`.
- Licht dit toe.
-
Van één van deze dozen is de hoogte 4 keer zo groot dan de zijden van het grondvlak en is de inhoud 1 liter.
Bereken de lengte van een zijde van het grondvlak in mm nauwkeurig.
-
Je ziet hier acht functies. Welke zijn gelijk? (Neem aan dat `x > 0`.)
`y_1 = (4x^5)/(x^2)` `y_2 = 4 * sqrt(x)` `y_3 = 4x^3` `y_4 = (100x)/(sqrt(x))`
`y_5 = 4x^(1//2)` `y_6 = 1/2 x * 4x^2` `y_7 = 2 * x^3` `y_8 = 100x^(1//2)`
-
Schrijf de volgende functies in de vorm `y = a * x^b`.
- `y_1 = 4x^8 * 8x^3`
- `y_2 = (4x^8) // (8x^3)`
- `y_3 = (-3x^4)^3`
- `y_4 = x^3 sqrt(x) * 3x^2`
-
Een formule voor inhoud `I` van een bol met straal `r` is: `I = 4/3 pi r^3`.
- Bereken de inhoud van een bol met een diameter van 50 cm.
- Bereken diameter van een bol met een inhoud van 1 liter.
- Stel een formule op voor `r` afhankelijk van `I`.
- Hoeveel keer zo groot wordt de straal van de bol als de inhoud 3 keer zo groot wordt?
hemel-
lichaam | diameter
(`xx 10^6` m) |
| Mercurius | 4,866 |
| Venus | 12,160 |
| Aarde | 12,756 |
| Maan | 3,476 |
| Mars | 6,772 |
| Jupiter | 142,72 |
| Saturnus | 120,74 |
| Uranus | 51,2 |
| Neptunus | 45,4 |
| Pluto | 2,2 |
-
In het informatieboek staat deze formule voor de kijkafstand `a` (in m) afhankelijk
van de hoogte h (in m) waarop je je boven het grondoppervlak bevindt: `a = 3572 * h^(1//2)`.
Deze formule geldt alleen op de aarde. Als je op een andere planeet of op de
maan staat, moet de formule worden aangepast aan de straal van het betreffende
hemellichaam.
Het verband wordt dan beschreven met de formule: `a = 3572 * c * h^(1//2)`.
De waarde van `c` hangt af van de diameter van het hemellichaam.
Op de aarde kun bij een bepaalde hoogte ongeveer 3,67 keer zo ver kijken als op de maan. Dat getal is bij benadering gelijk aan de verhouding van hun twee diameters. Eenzelfde berekening kun je maken voor de overige hemellichamen.
-
Leg uit waarom de constante `c` in deze formule kleiner is dan 1 voor de kijkafstand op de maan.
-
Bepaal de waarde van `c` in de formule voor de kijkafstand op de maan. Licht je antwoord toe.
-
Bepaal de waarde van `c` in de formule voor de kijkafstand op Saturnus. Licht je antwoord toe.
-
Teken de grafieken voor de kijkafstand op verschillende denkbeeldige hemellichamen, voor `c = 0,25`, `c = 0,75` en `c = 1,25` op de grafische rekenmachine.
Bedenk eerst welke grafiek de onderste en welke grafiek de bovenste zal worden en kijk naderhand of je gelijk had.
-
Er is een constante `c` waarvoor geldt dat de kijkafstand vanaf een hoogte van 60 m boven het grondoppervlak ongeveer 20 km is. Hoort deze waarde van `c` bij een hemellichaam dat groter of kleiner is dan de aarde?
Toetsen
-
Schrijf de volgende functies in de vorm `y = a * x^b`.
- `y_1 = (15x^2)/x * 8x^3`
- `y_2 = 3x * sqrt(x)`
- `y_3 = (6x^3) // (x^2)`
- `y_4 = (2x^2)^(1//2)`
-
De huidoppervlakte `H` van een schaap hangt af van zijn gewicht `G` (in kg) volgens de formule: `H = 8,4 * G^(2//3)`.
-
Laat zien, dat bij een twee keer zo groot gewicht de huidoppervlakte ongeveer 1,6 keer zo groot wordt.
-
Laat zien, dat uit deze formule kan worden afgeleid: `G = 0,041 * H^(3//2)`.
-
Als de huidoppervlakte van een gemiddeld volwassen schaap twee keer zo groot is als die van een gemiddeld jong schaap, hoeveel keer zo zwaar is zo’n volwassen schaap dan?


