Totaalbeeld

Samenvatten

Je hebt nu het onderwerp Exponentiële verbanden doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

Begrippenlijst:

41: exponentiële groei — groeifactor — macht, grondtal, exponent
42: rekenregels voor machten
43: algemene formule voor exponentiële groei
44: exponentiële functie — exponentiële vergelijking en ongelijkheid
45: logaritmische schaal — enkellogaritmisch papier

Activiteitenlijst:

41: formule voor exponentiële groei opstellen bij gegeven groeifactor (groeipercentage) en beginwaarde
42: rekenregels voor machten toepassen — groeifactoren omrekenen naar grotere tijdseenheden
43: groeifactoren omrekenen naar kleinere tijdseenheden
44: eigenschappen van exponentiële functies toepassen — exponentiële functie opstellen bij gegeven punten van de grafiek
45: werken met logaritmische schalen — formule opstellen bij exponentiële groei bij gegeven tabel, punten of grafiek (op enkellogaritmisch papier)

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Exponentiële verbanden > Totaalbeeld > Achtergronden

Testen

Het aantal passagiers dat jaarlijks gebruik maakt van een vliegveld groeit de laatste jaren met 2% per jaar. In 2000 maakten 43000 passagiers gebruik van het vliegveld.
1. Hoeveel bedraagt de groeifactor per jaar?
2. Geef een formule voor het aantal passagiers `p` op tijdstip `t` in jaren na 2000.
3. Als de groei zo doorgaat, hoe lang duurt het dan voor het huidige aantal passagiers verdubbeld is?
4. Hoeveel passagiers waren er in 1997?
5. Hoeveel bedraagt de groeifactor per tien jaar?
6. Hoe groot is is de groeifactor per kwartaal?

In de gemeente Z groeit het aantal inwoners sinds 2000 met ongeveer 3,2% per jaar. In het jaar 2000 had de gemeente Z in totaal 97452 inwoners. Het aantal woningen in Z bedroeg toen 35505.
1. Geef een formule voor het aantal inwoners `A` van Z waarbij je er van uitgaat dat de groei onverminderd met hetzelfde percentage doorgaat.
2. Neem aan dat alle inwoners van Z in één van die 35505 woningen woonden. Hoeveel inwoners telde Z in 2000 gemiddeld per woning? (Rond af op twee decimalen.)
3. De gemeente Z liet om de bevolkingsgroei op te vangen jaarlijks gemiddeld 1350 woningen bijbouwen. Als je het aantal mensen per woning constant houdt, hoeveel mensen kan Z dan jaarlijks meer huisvesten?
4. Tot welk jaar kan Z zijn bevolking huisvesten als er gemiddeld 1350 woningen per jaar bijkomen en het aantal personen per woning ongewijzigd blijft?

Een doorzichtige kunststof absorbeert een deel van het licht dat er doorheen valt. Elke laag van 1 cm absorbeert 20% van het licht.
1. Met welke factor wordt de hoeveelheid licht vermenigvuldigd per cm kunststof?
2. Hoeveel procent van het licht wordt geabsorbeerd door een laag van 2,5 cm dikte?
3. Hoe dik moet de laag kunststof zijn om 90% van het licht te absorberen?
4. Met welke factor wordt de hoeveelheid licht vermenigvuldigd per mm kunststof?

Iemand haalt een fles melk uit de koelkast en zet er een fles cola voor in de plaats. De temperatuur van de fles melk neemt hierdoor langzaam toe tot kamertemperatuur, de temperatuur van de fles cola neemt juist af tot koelkasttemperatuur. De formules voor de temperaturen `T_1` en `T_2` (in graden Celsius) in de flessen, afhankelijk van de tijd `t` (in minuten) zien er zo uit:
`T_1 = 19 - 13 * 0,78^t`
`T_2 = 6 + 13 * 0,78^t`
1. Teken de grafieken van beide formules in één figuur. Laat `t` hierbij lopen van 0 tot 25.
2. Welke van de formules hoort bij de fles melk, en welke bij de fles cola? Licht je antwoord toe.
3. Wat is de asymptoot van de grafiek van de temperatuur van de fles cola?
4. Wat is de asymptoot van de grafiek van de temperatuur van de fles melk?
5. Hoeveel bedraagt de kamertemperatuur?
6. Vanaf welk tijdstip is de cola kouder dan de melk?

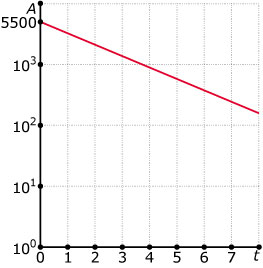In sommige dorpen in delen van Rusland is weinig werkgelegenheid meer en daarom trekken steeds meer mensen er weg. In de grafiek is het aantal inwoners `A` van zo'n dorp uitgezet tegen de tijd `t` in jaren. Het tijdstip `t = 0` komt overeen met het jaar 2000.
1. Waaruit concludeer je dat er sprake is van een exponentieel verband?
2. Waren er in 2006 meer of minder dan 600 inwoners?
3. Bepaal de groeifactor en geef een formule voor het aantal inwoners als functie van de tijd (in jaren).
4. Iemand doet de volgende uitspraak: "Het aantal inwoners wordt nooit nul, maar komt wel steeds dichter bij nul."
  Geef argumenten waarom je het met deze persoon eens of oneens bent.

Toepassen

Radioactief verval
Een natuurkundige toepassing van exponentiële functies vind je bij radioactiviteit. Lees hierover in
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Exponentiële verbanden > Totaalbeeld > Toepassingen
Het element radium-228 is radioactief. Het vervalt tot het niet-radioactieve radium- 224. Van een willekeurige hoeveelheid radium-228 wordt in één jaar 10% omgezet in radium-224. Een laboratorium heeft in het jaar 2001 1000 mg radium-228.
1. Geef een formule van `R`, de hoeveelheid radium-228 in mg, op tijdstip `t` in jaren.
2. Bereken hoe lang het duurt (tot op een maand nauwkeurig) totdat er van de 1000 mg radium-228 nog 800 mg over is.
3. Bij radioactieve stoffen zijn scheikundigen vaak geïnteresseerd in de halveringstijd. Bereken de halveringstijd van radium-228.
4. Als je de halveringstijd weet kun je overzien hoe snel het verval gaat. Schat met behulp van de halveringstijd hoe lang het duurt tot 750 mg radium-228 is omgezet in radium-224.

Wereldbevolking
Omstreeks 1970 bedroeg de wereldbevolking ongeveer 3,6 miljard en zij groeide per jaar met 2,1%.
1. Hoe groot was toen de groeifactor?
2. Als we ervan uitgaan dat die groeifactor door de jaren heen gelijk is gebleven, hoeveel mensen leefden er dan in 1971, 1988, 1900 en het jaar 0?
3. `B` is de bevolking na `t` jaren, gerekend vanaf 1970 (`t=0`). Geef `B` als functie van `t` door een formule.
4. Je hebt nu een model van de bevolkingsgroei gemaakt, gebaseerd op gegevens uit 1970. Volgens het Wereldbevolkingsrapport uit 1999 is in 2050 het aantal mensen op Aarde nog geen 9 miljard. Klopt dat met de formule die je bij b hebt gevonden?
5. Waaraan kun je zien dat de bevolkingsgroei dan niet meer exponentieel loopt? Kun je daar redenen voor geven?

Zuurgraad
In de scheikunde wordt het begrip zuurgraad gebruikt om aan te geven of een bepaalde oplossing meer of minder zuur of basisch is. De zuurgraad wordt voorgesteld door pH en weergegeven op een logaritmische schaal.
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Exponentiële verbanden> Totaalbeeld > Toepassingen
1. Bij geconcentreerd zwavelzuur is [H⁺] = 18 Mol/L. Hoeveel bedraagt de zuurgraad?
2. Huishoudammonia (verdunde ammonia) heeft een zuurgraad van 11,5. Hoeveel bedraagt de H⁺ concentratie in Mol/L?
3. Zure regen heeft een pH-waarde van 4. Hoeveel bedraagt de H⁺ concentratie van zure regen?
4. Vanaf welke H⁺ concentratie is de zuurgraad negatief? Is de oplossing dan heel zuur of juist niet?
5. De aanduiding pH-neutraal op cosmetische producten betekent iets anders dan een pH van 7. Het geeft aan dat het product een pH heeft die overeenkomt met de natuurlijke pH van de huid. De natuurlijk pH van de huid is ongeveer 5,5. Hoeveel bedraagt de H⁺ concentratie dan?

Examenopgaven

Ureumgehalte
De kwaliteit van het water in zwembaden wordt onder andere beooreeld op grond van het ureumgehalte. Ureum komt in het water via zweet en urine. Metingen hebben aangteoond dat bij 1000 bezoekers per dag de hoeveelheid ureum in het water op die dag met 500 gram toeneemt.
Om te voorkomen dat er te veel ureum in het water komt, moet er zo ververst worden dat de wettelijke norm van 2 gram ureum per cm³ water niet overschreden wordt. In een model gaan we er van uit dat dagelijks 1000 bezoekers een bad van 1000 m³ bezoeken.
Voor verversing rekent men 30 liter per persoon per dag. Dat betekent in dit model dat 's nachts 30 m³ ververst wordt (dus 3% van het totaal).
We beginnen de eerste dag met 0 gram ureum in het water. Aan het eind van de dag zit er 500 gram ureum in het water. Na verversen is er dan aan het begin van de tweede dag 485 gram ureum over.
1. Laat door berekening zien dat er aan het begin van de derde dag ruim 955 gram ureum in het water zit.
2. In de loop van welke dag wordt de wettelijke norm overschreden? Licht je antwoord toe.
Het blijkt dat 30 liter per bezoeker per dag verversen niet voldoende is. In plaats van 30 liter wordt daarom 200 liter genomen.
1. Stel `U` is de hoeveelheid ureum aan het begin van een zekere dag. Toon aan dat de hoeveelheid ureum aan het begin van de daaropvolgende dag gelijk is aan `0,8U + 400`.
We starten in het model weer met 0 gram ureum aan het begin van de eerste dag. De hoeveelheid ureum in gram (`U_n`) aan het begin van de `n`de dag kan rechtstreeks berekend worden met de formule:
`U_n = 2000 - 2500 * 0,8^n`
1. Leg uit met behulp van deze formule dat aan het begin van elke dag aan de wettelijke norm voldaan wordt.
2. In de loop van de dag kan de wettelijke norm wel worden overschreden. Bereken op welke dag dat voor het eerst gebeurt.
(bron: examen wiskunde A havo 1989, tweede tijdvak)

Sparen, sparen en sparen

Nederland is een echt spaarland. Jaarlijks worden er miljarden euro's gestort op spaarrekeningen.
Er zijn verschillende soorten spaarrekeningen. In deze opgave bekijken we er drie: de groeirekening, de depositorekening en de renteklimrekening.
We storten op elk van de drie spaarrekeningen een bedrag van € 10000 dat voor een periode van 10 jaar op de spaarrekening blijft staan.

Groeirekening

De groeirekening is de bekendste soort. Het rentepercentage op deze rekening is 3,5% per jaar. Het is een 'rente op rente'-rekening: na een jaar wordt de rente bijgeschreven op de rekening, zodat het volgende jaar rente wordt berekend over een hoger bedrag `G`. Na elk jaar wordt het bedrag op de rekening dus hoger. Het bedrag `G` dat na`t` jaar op de groeirekening staat kun je bereken met de formule: `G = 10000 * 1,035^t`. Het bedrag op de groeirekening is na 10 jaar nog niet verdubbeld. Maar als je de rekening nog langer laat doorlopen, komt er een jaar dat het bedrag op de rekening voor het eerst twee keer zo hoog is. Het bedrag is zelfs nog hoger dan € 20000.

Bereken na hoeveel jaar dat is.

Depositorekening

De depositorekening is een spaarrekening met een rentepercentage van 4,0% per jaar. De rente over elk jaar is € 400. Dat bedrag wordt steeds bijgeschreven op een aparte betaalrekening. Op de betaalrekening krijg je geen rente, zodat het bedrag op de betaalrekening lineair toeneemt.
De rente van 4,0% lijkt gunstiger dan een rente van 3,5%. Toch heb je na toen jaar bij de depositorekening in totaal minder rente gekregen dan bij de groeirekening. Een bank introduceert een nieuwe depositorekening die in tien jaar evenveel rente oplevert als de groeirekening.

Bereken het rentepercentage per jaar van die nieuwe depositorekening. Geef je antwoord in één decimaal.

Renteklimrekening

De renteklimrekening is een soort depositorekening. Ook hier wordt jaarlijks de rente bijgeschreven op een aparte betaalrekening die geen rente oplevert.
Bij de renteklimrekening wordt het rentepercentage elk jaar hoger.
In deze tabel kun je aflezen welke bedragen er na `t` jaar sparen op de renteklimrekening `R` en op de betaalrekening `B` staan.

t	0	1	2	3	4	5	6	7	8	9	10
R	10000	10000	10000	10000	10000	10000	10000	10000	10000	10000	10000
B	0	300	615	950	1310	1700	2130	2615	3165	3775	4475

In de volgende volledige tabel staan de rentepercentages voor het t-de jaar.

t-de jaar	1	2	3	4	5	6	7	8	9	10
rentepercentage	3,00	3,15	3,35	3,60	3,90	4,30

Bereken het rentepercentage voor het 7e jaar. Geef je antwoord in twee decimalen.
De renteklimrekening geeft in tien jaar € 4475 rente. Wat dit betreft is het de beste van de drie spaarrekeningen. De groeirekening is de op één na beste.
Bereken het rentepercentage per jaar dat een groeirekening met hebben om in 10 jaar € 4475 rente te geven. Geef je antwoord in twee decimalen.

(bron: examen wiskunde A havo 2004, tweede tijdvak)

De wet van More

Het Amerikaande bedrijf Intel is een zeer grote producent van computerchips. Gordon Moore was in 1968 één van de oprichters van het bedrijf,
Deze opgave gaat over het aantal transistoren in een computerchip. (Een transistorenis een elektronische schakeling.)
In 1965 deed Moore daar een voorspelling over:
"Het aantal transistoren in een computerchip zal tussen 1965 en 1975 exponentieel groeien".
Moore heeft meer dan gelijk gekregen: de voorspelling is zelfs tot het jaar 2000 uitgekomen! Zijn voorspelling is men de Wet van Moore gaan noemen.
In de tabel zie je hoeveel transistoren er in de chips van Intel zitten. Ook zie je in welk jaar die chips op de markt zijn gebracht.

introductiejaar	naam chip	aantal transistoren
1971	4004	2250
1972	8008	2500
1974	8080	5000
1978	8086	29000
1982	286	120000
1985	386	275000
1989	486 DX	1180000
1993	Pentium I	3100000
1997	Pentium II	7500000
1999	Pentium III	24000000
2000	Pentium IV	42000000

In de tabel zie je dat het aantal transistoren tussen 1971 en 1972 met 250 toeneemt.
Stel dat het aantal transistoren in de jaren daarna lineair toe zou nemen met 250 per jaar.

In welk jaar zou dan het aantal van 5000 transistoren per chip zijn bereikt? Licht je antwoord toe.

In werkelijkheid is de toename dus exponentieel. Zo is in de periode van 1971 to 2000 het aantal transistoren per chip toegenomen van 2250 tot 42 miljoen.

Bereken hiermee de groeifactor per jaar in vier decimalen nauwkeurig.

De Wet van Moore in formulevorm is: `A = 2250 * 1,404^t`.
Hierin is `A` het aantal transistoren per chip en `t` de tijd in jaren met `t=0` in 1971. In de Pentium II-chip zitten volgens de tabel 7500000 transistoren. Dat het aantal transistoren wijkt nogal af van de voorspelling volgens de Wet van Moore.

Bereken hoeveel procent dit aantal afwijkt van de voorspelling volgende de formule van de Wet van Moore.
Met behulp van de formule kunnen we voorspellen wanneer er 1 miljard transistoren in een computerchip zitten. Bereken hoeveel jaar na 1971 dit het geval is.

(bron: examen wiskunde A havo 2005, eerste tijdvak)