Rekenen met machten

Inleiding

In de formules voor exponentiële groei komen machten voor. Om er mee te kunnen werken moet je dus met machten kunnen rekenen. Waarschijnlijk heb je dat wel geleerd, maar hier worden de belangrijkste rekenregels voor machten nog even opnieuw uitgelegd.

Je leert nu:

• rekenen met machten;
• de rekenregels voor machten toepassen bij exponentiële groei.

Je kunt al:

• werken met formules voor exponentiële groei en afname;
• werken met functies en grafieken.

Verkennen

De hoeveelheid bacteriën B (in gram) in een petrischaaltje groeit volgens de formule
B = 6 · 2^t.
Het startmoment van meten t = 0 is vandaag om 12:00 uur.

> Hoeveel lagen papier zijn er na 20 keer dubbelvouwen?
> Waarom zal dit met een A4tje nooit lukken?

Stel dat het onbegrensde vel papier 0,15 mm dik is.

> 3 uur na t = 0 heb je 6 · 2³ gram bacteriën. Hoeveel heb je er nog weer 5 uur later?
> Hoe bereken je de hoeveelheid bacteriën die je dan hebt in één keer vanaf t = 0?
> De groeifactor per uur is 2. Hoeveel is de groeifactor per dag?
> Wat stelt (2²⁴)⁷ in dit verband voor?

Uitleg

Voor het aantal bacteriën B na t uur geldt de formule B = 600 · 2^t.
Door te denken aan bacteriegroei en deze functie B kun je een aantal rekenregels voor machten afleiden.

Allereerst heb je op t = 0 volgens de formule 600 · 2⁰ bacteriën. Omdat je weet dat dit precies 600 moet zijn is: 2⁰ = 1.

Na 3 uur heb je 600 · 2³ en 4 uur later 600 · 2³ · 2⁴. Dit is het aantal bacteriën na 7 uur, dus 6 · 2⁷. Conclusie: 2³ · 2⁴ = 2⁷. Als je machten vermenigvuldigt tel je de exponenten op.

Na 7 uur heb je 600 · 2⁷ en 4 uur eerder 600 · 2⁷ / 2⁴. Dit is het aantal bacteriën na 3 uur, dus 600 · 2³. Conclusie: 2⁷ / 2⁴ = 2³. Als je machten deelt trek je de exponenten af.

De groeifactor per uur is 2. Per drie uur is die groeifactor 2³ = 8.
Het aantal bacteriën na 12 uur kun je op twee manieren berekenen: 600 · 2¹² of 600 · 8⁴. Dus moet (2³)⁴ = 2¹². Bij machten van machten vermenigvuldig je de exponenten.

Deze rekenregels gelden heel algemeen voor alle grondtallen en exponenten. Alleen met grondtal 0 moet je voorzichtig zijn...

‡

Opgaven

1. Bekijk het verhaal van de bacteriegroei in de Uitleg.
   1. Hoeveel bacteriën heb je na 12 uur? En hoeveel heb je er vijf uur later?
   2. Over welke rekenregels voor machten gaat opgave a?
   3. Hoeveel bedraagt de groeifactor per 4 uur? Van welke rekenregel is dit een voorbeeld?
   4. Hoeveel bedraagt de groeifactor per dag?


2. Waar of niet waar?
   1. `2^3 * 2^5 = 2^(15)`
   2. `11^(50) * 11^(50) = 11^(100)`
   3. `3^7 + 2^7 = 5^7`
   4. `(2^2)^3 = 2^6`

Theorie

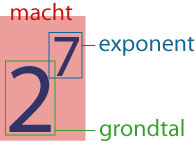
Bij exponentiële groei werk je met machten: vermenigvuldig je t keer hetzelfde getal g, dan schrijf je dat als g^t. Dit is een macht, de groeifactor g heet het grondtal, n heet de exponent, waarbij t (voorlopig) een positief geheel getal is.

Voor t = 0 is de afspraak: g⁰ = 1.

In het algemeen geldt voor een willekeurig grondtal g en willekeurige positieve gehele n en m de volgende rekenregels:

• gⁿ · g^m = g^n + m

• $\frac{g^n}{g^m}=g^{n-m}$

• (gⁿ)^m = g^n · m

‡

Voorbeeld 1

Als één macht schrijven gaat zo:

• (2³)⁴ · 2¹⁰ = 2¹² · 2¹⁰ = 2²²

• $\frac{3^{16}}{3\cdot 3^4}$ = $\frac{3^{16}}{3^5}$ = 3¹¹

• 2¹⁰ + 7 · 2¹⁰ = 8 · 2¹⁰ = 2³ · 2¹⁰ = 2¹³

• 0,9⁴ · (0,9²)³ = 0,9⁴ · 0,9⁶ = 0,9¹⁰

‡

Voorbeeld 2

Een spaartegoed staat uit tegen 0,5% rente per maand.
De bank wil de rente per half jaar bijschrijven of zelfs jaarlijks.
Met welke rentepercentages moeten ze dan werken? (Geef beide percentages in twee decimalen nauwkeurig.)

Antwoord

De groeifactor van het spaartegoed per maand is 1,005.

De groeifactor per half jaar is dan: 1,005⁶ ≈ 1,0304.
Het rentepercentage per half jaar is dus 3,04%.
Dat is iets meer dan 6 × 0,5 = 3%.

Op dezelfde manier is de groeifactor per jaar (1,005⁶)² of 1,005¹² en dat is ongeveer 1,0617.
Het rentepercentage per jaar is dus 6,17%.

‡

Voorbeeld 3

Bereken `(256^100 * 64^200)/(1024^199)`.

Antwoord

Was je zo blij met je rekenmachine, laat ie je in de steek! Of niet soms?
Dit moet je zonder rekenmachine kunnen, gewoon met de rekenregels en met machten van 2.
Tel maar na: 256 = 2⁸, 64 = 2⁶ en 1024 = 2¹⁰.

En dus staat hier: `((2^8)^100 * (2^6)^200)/((2^10)^199) = (2^800 * 2^1200)/(2^1990) = (2^2000)/(2^1990) = 2^10 = 1024`.

Zo zie je maar weer dat de mens machtiger is dan zijn machine...

‡

Opgaven

3. In Voorbeeld 1 gebruik je de rekenregels voor machten. Schrijf de volgende uitdrukkingen als één macht:
   1. `2^3 * (2^4)^2`
   2. `4^5 * 2^3`
   3. `((5^2)^4)/(5 * 5^3)`
   4. `(5^6)/(5^2 * 5^4)`


4. In Voorbeeld 2 zie je hoe je omrekent van een groeifactor per maand naar een groeifactor per half jaar en een groeifactor per jaar. Bekijk ook de bijbehorende groeipercentages. De groeifactor per uur is 1,02.
   1. Hoeveel bedraagt het groeipercentage per uur?
   2. Hoeveel bedraagt de groeifactor per dag? En het groeipercentage per dag?
   De groeifactor per uur wordt 0,91.
   3. Hoeveel bedraagt het groeipercentage per uur?
   4. Hoeveel bedraagt de groeifactor per dag? En het groeipercentage per dag?


5. Iemand zet op 1-1-2000 op een bankrekening € 800,- tegen 6% rente. De rente wordt jaarlijks op de bankrekening bijgeschreven. Er wordt verder geen geld op de bankrekening gestort of geld van de bankrekening gehaald.
   1. Wat is de groeifactor per jaar van het tegoed op de bankrekening?
   2. Hoeveel staat er op de bankrekening op 1-1-2005? Laat zien hoe je dat berekent.
   3. Welke formule geldt voor het spaartegoed `S(t)`, waarin `t` de tijd in jaren na 1-1-2000 is?
   4. Hoe groot is de groeifactor per vijf jaar? Bereken ook het groeipercentage per vijf jaar.
   5. Laat met berekeningen zien dat je op de volgende manieren het tegoed op 1-1-2020 kunt berekenen:
      • `t=20` invullen in de formule;
      • het tegoed op 1-1-2000 vermenigvuldigen met de groeifactor per 20 jaar;
      • het tegoed op 1-1-2000 vijf keer vermenigvuldigen met de groeifactor per 4 jaar;
      • het tegoed op 1-1-2000 vier keer vermenigvuldigen met de groeifactor per 5 jaar.


6. Bekijk Voorbeeld 3.
   Gebruik de rekenregels voor machten om de uitdrukkingen als één macht te schrijven:
   1. `(2^214 * 2^80)/((2^12)^24)`
   2. `(1/3)^83 * (3^40)^2`

Verwerken

7. In een ondiep meer van 1000 km² begint riet te groeien. Op 1-1-2005 is de oppervlakte van het met riet begroeide deel 1 km².
   Vanaf dat moment wordt de oppervlakte van het met riet begroeide deel gemeten.
   In 2010 constateert men dat de oppervlakte van het met riet begroeide deel elk jaar twee keer zo groot is geworden. Ga ervan uit dat het riet zich in hetzelfde tempo blijft uitbreiden.
   1. Hoeveel bedraagt de groeifactor per jaar?
   2. Maak een tabel voor de met riet bedekte oppervlakte voor de eerste vijf jaar.
   3. Hoe groot is de groeifactor per tien jaar?
   4. Na hoeveel jaar is het hele meer begroeid met riet?


8. Schrijf als één macht:
   1. `2^4 * 2^3`
   2. `(2^3)^2 * 2^4 + 2^3 * 2^7`
   3. `(2^512)/(2^509)`
   4. `(2^53)^3 * (1/2)^100`


9. De concentratie van een bepaalde vervuilende stof in het water neemt langzaam af met een vast percentage van 13% per uur. Op `t=0` is de concentratie 150 mg per liter.
   1. Hoeveel bedraagt de groeifactor per uur? Stel een formule op voor de concntratie `C` als functie van de tijd `t` in uren.
   2. Na hoeveel uur is de concentratie gehalveerd?
   3. Met hoeveel procent neemt de concentratie per dag af?


10. Schrijf als één macht:
    1. `(3^214)/(3^211)`
    2. `3^110 * (1/3)^109`
    3. `((3^16)^10)/(3^100 * 3^60)`
    4. `(3/4)^235 * (4/3)^236`


11. Iemand koopt voor € 5000,= aandelen. In de volgende maanden blijkt dat de waarde van de aandelen exponentieel afneemt. Na één maand zijn de aandelen € 600,= minder waard geworden.
    1. Hoeveel procent is 600 van 5000?
    2. Bereken de groeifactor van de waarde van de aandelen.
    3. Maak een tabel met de waarde van de aandelen voor de eerste vijf maanden.
    4. Met welk getal moet je de waarde na vijf maanden vermenigvuldigen om de waarde na tien maanden te krijgen? Bereken de waarde na tien maanden.
    5. Hoeveel is de groeifactor per tien maanden? En per vijftien maanden?
    6. Hoeveel maanden duurt het ongeveer voor de waarde van de aandelen is gehalveerd?

Testen

12. Iemand betaalt een huur van € 950,- (per maand). Er wordt een jaarlijkse huurverhoging verwacht van 4%.
    1. Stel een formule op waarmee je voor volgende jaren de huur per maand kunt berekenen.
    2. Maak een tabel waarmee je kunt uitzoeken hoe lang het duurt tot de huur meer dan € 1300,- per maand is geworden.
    3. Hoe groot is de groeifactor van de maandelijkse huur per 4 jaar?
    4. Bereken met behulp van de groeifactor per 4 jaar de groeifactor per 20 jaar.
    5. Bereken het groeipercentage per 20 jaar.
    6. Na hoeveel jaar is de huur per maand voor het eerst meer dan verdubbeld?


13. Schrijf als één macht: `(17^11 * 17^54)/((17^4)^21)`.
    


14. Een bepaalde soort vlinders wordt in een bepaald natuurgebied zijn voortbestaan bedreigd. In 2007 werden er nog 4600 exemplaren van geteld. In de volgende jaren blijkt dat de aantallen elk jaar met 12% afnemen.
    1. Stel een formule op voor het aantal vlinders van die soort `N(t)`, waarin `t` de tijd in jaren na 2007 is.
    2. Na hoeveel jaar is de het aantal vlinders minder dan 1000 geworden?
    3. Bereken het groeipercentage per vijf jaar.
    4. Met welk getal moet je het aantal vlinders na vijf jaar vermenigvuldigen om het aantal na tien jaar te krijgen? Bereken het aantal vlinders na tien jaar.
    5. Bereken het groeipercentage per tien jaar.